Ontario Alignment By Overall Expectation
Finding the Equation of a Line Given Two Points
This 3 Act Math Task is yet another sequel to the Stacking Paper and Stacking Paper – Sequel 3 Act Math Tasks where we look at linear relations with respect to a real world situation involving packages of paper stacked into a tower.
While the original task begins with a direct variation requiring only basic proportional reasoning skills, the previous sequel had students looking at a partial variation linear relation with an initial value being the height of a table and were required to use the thickness of one package of paper (slope) and the height of the stack on a table (a point) to determine the height of the table. In this task, students are given two stacks of paper (thus two points) and must use them to find the height of a different table.
To access the other tasks in this series, see below:
- Stacking Paper – Direct Variation (y-intercept equal to 0)
- Stacking Paper Sequel – Partial Variation (y-intercept not equal to 0)
- Thick Stacks – Finding the Equation of a Line Given Two Points
Act 1: Introducing The Problem
Stacking Paper on a Table
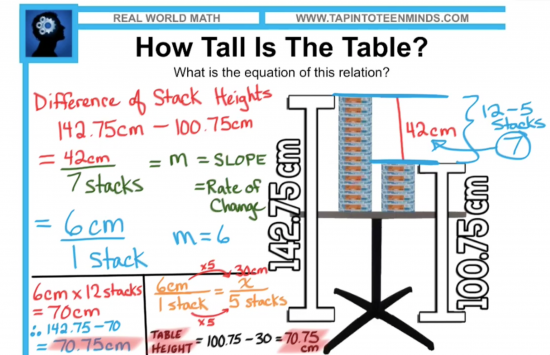
In the first act, students will view the image of 12 packages of paper and 5 packages of paper stacked on a shorter table than that used in the Stacking Paper Sequel problem:
As usual, give students some time to chat with an elbow partner to decide what question they believe will be asked in this problem. You can try to lead the discussion towards a specific question, or work with what they come up with.
Act 2: Reveal Some Information
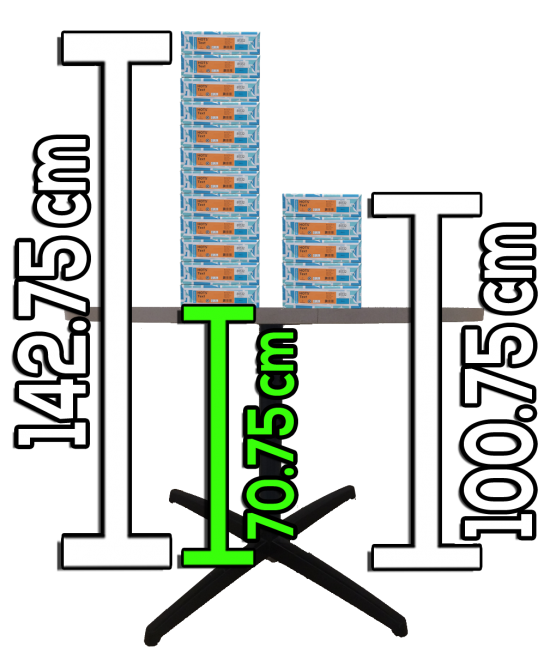
Height of 12 Stacks and 5 Stacks on a Table
Give students the following image to ponder with their peers:
Since it is likely that they have completed the Stacking Paper or Sequel tasks, it might be useful to show them that the paper packages stacked here have a different thickness in comparison to the previous two tasks:
The question I want my students to answer here is:
How tall is the table?
At this point, I hope students can quickly identify that the height of the table is the y-intercept of this linear relation and thus can use their prior knowledge to help them get started using the inquiry/discovery process.
Stacking Paper Sequel Inquiry / Discovery
The prior knowledge my students had before completing this task:
- an understanding of linear relations,
- an understanding of slope as a rate of change,
- an understanding of the initial value / y-intercept of a line,
- an understanding of how to use their knowledge via logic, table of values and a graph to solve problems, and
- an understanding of how to use slope and a point to find the y-intercept in order to create a linear equation.
Here are some approaches my students have used when solving this problem:
Logic / Arithmetic:
Students in my class used this method almost exclusively and all students were successful finding the solution.
Table of Values:
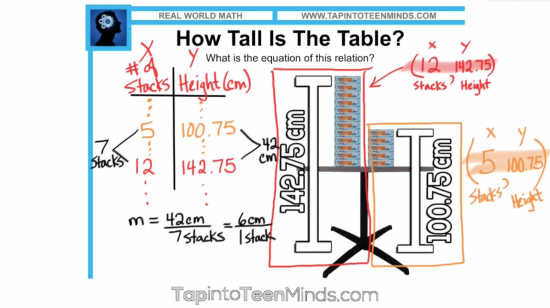
A couple of students set up what appeared to be a table of values to help them find the slope of the line by using the differences in the table.
After finding slope, they could then use the method of finding the y-intercept when given slope and a point as we learned in the Stacking Paper Sequel task to find the height of the table:
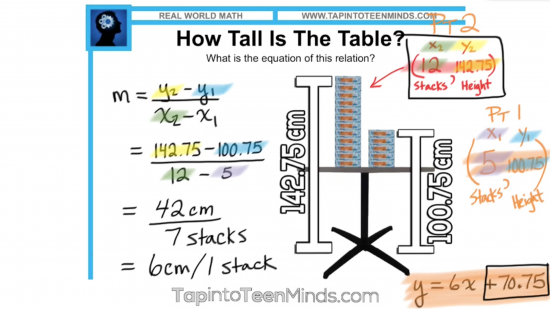
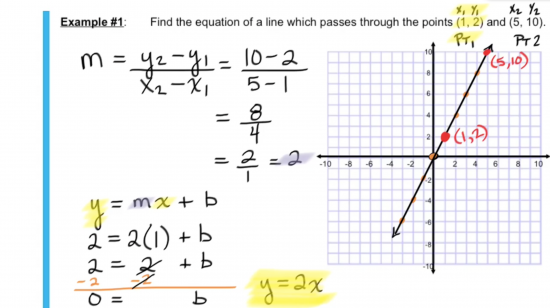
Algebraic Method Using The Slope Formula:
Although we had previously introduced the formula for slope of a line, we have focused primarily on the use of rise over run as well as finding slope using the differences in a table and thus no students utilized the formula for slope:
Act 3: Reveal the Solution
The Height of the Table Is…
Sequel / Extenions:
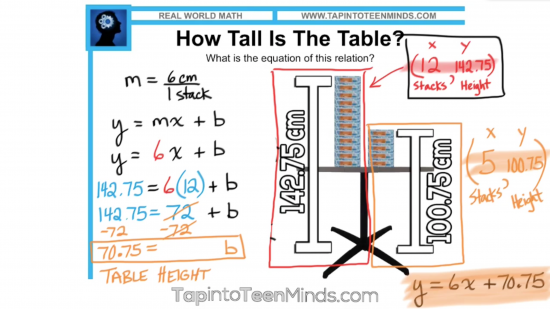
Finding the Equation of the Line
Since the majority of our grade 9 academic and applied curriculum involves linear relations and equations of lines, it seems logical here for students to take their knowledge of the height of the table and find the equation representing this linear pattern.
A possible question could be:
How many stacks of paper you would need to reach the top of the school, flagpole or CN Tower?
Obviously, the more stacks of paper needed to find the answer, the more convenient the equation will seem!
Check out this video summary that goes through the problem:
Comparing To The Textbook:
More and more I am really disappointed with how lame the questions in our textbooks and resource guides are. For years, I have been assigning questions that have no context or purpose. Sure, you could argue that there is no need for us to determine the height of a table, but it sure beats this:
This Task Is Now in a Multi-Touch Book!
Learn more about what’s inside this multi-touch book for iBooks here. Or, consider using this task in an interactive way via Google Sites.
New to Using 3 Act Math Tasks?
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Access Other Real World Math Tasks
Search More 3 Act Math Tasks
Grade 2 [2.B1.1, 2.B1.3, 2.B2.1, 2.B2.2, 2.B2.3, 2.B2.4, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3]
Grade 3 [3.B1.5, 3.B2.1, 3.B2.3, 3.B2.7, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3]
Grade 4 [4.B2.1, 4.B2.4, 4.E2.5, 4.E2.6, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 5 [5.B1.7, 5.B2.9, 5.D1.3, 5.D1.6, 5.E2.6, 5.F1.2, 5.F1.5, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 6 [6.B2.12, 6.B2.9, Data Management and Probability - DP3, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 7 [7.B1.3, 7.B1.4, 7.B1.7, 7.B2.2, 7.B2.3, 7.C1.1, 7.C1.2, 7.C1.3, 7.C1.4, 7.D1.6, Data Management and Probability - DP3, Geometry and Spatial Sense - GS1, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 8 [8.B1.4, 8.B2.5, 8.C1.1, 8.C1.2, 8.C1.3, 8.C1.4, Data Management and Probability - DP1, Data Management and Probability - DP3, Geometry and Spatial Sense - GS2, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 9 [9.B3.5, 9.C3.1, 9.C3.2, 9.C3.3]
Kindergarten [k.15.1, k.15.10, k.15.2]
MAP4C [Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MAT1LMAT2LMBF3C [Data Management - DM1, Data Management - DM2, Geometry and Trigonometry - GT1, Geometry and Trigonometry - GT2, Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MCF3M [Exponential Functions - EF2, Quadratic Functions - QF1, Quadratic Functions - QF2, Quadratic Functions - QF3, Trigonometric Functions - TF1, Trigonometric Functions - TF3]
MCR3U [Characteristics of Functions - CF1, Characteristics of Functions - CF2, Exponential Functions - EF2, Exponential Functions - EF3, Trigonometric Functions - TF3]
MCT4C [Exponential Functions - EF1, Trigonometric Functions - TF3]
MCV4U [Derivatives and Their Applications - DA2]
MDM4U [Counting and Probability - CP2, Organization of Data For Analysis - DA2, Probability Distributions - PD1, Statistical Analysis - SA1, Statistical Analysis - SA2]
MEL4EMFM1P [Linear Relations - LR1, Linear Relations - LR2, Linear Relations - LR3, Linear Relations - LR4, Measurement and Geometry - MG1, Measurement and Geometry - MG2, Measurement and Geometry - MG3, Number Sense and Algebra - NA1, Number Sense and Algebra - NA2]
MFM2P [Measurement and Trigonometry - MT1, Measurement and Trigonometry - MT2, Measurement and Trigonometry - MT3, Modelling Linear Relations - LR1, Modelling Linear Relations - LR2, Modelling Linear Relations - LR3, Quadratic Relations in y = ax^2 + bx + c Form - QR1, Quadratic Relations in y = ax^2 + bx + c Form - QR2, Quadratic Relations in y = ax^2 + bx + c Form - QR3]
MHF4U [Characteristics of Functions - CF3, Exponential and Logarithmic Functions - EL2, Exponential and Logarithmic Functions - EL3]
MPM1D [AG3, Analytic Geometry - AG1, Analytic Geometry - AG2, LR1, LR2, LR3, MG1, MG2, MG3, NA1, Number Sense and Algebra - NA2]
MPM2D [AG1, AG2, AG3, QR2, Quadratic Relations - QR3, Quadratic Relations - QR4, T2, T3]
Functions [F-BF.1, F-BF.3, F-IF.4, F-LE.1, F-LE.2, F-LE.3, F-TF.5]
Geometry [G-C.5, G-C.8, G-C.9, G-GMD.3, G-GMD.4, G-GPE.4, G-GPE.5, G-GPE.7, G-MG.1, G-MG.2, G-SRT.11]
Grade 1 [1.NBT.4, 1.OA.1, 1.OA.6, 1.OA.A.1, 1.OA.B.3, 1.OA.B.4, 1.OA.C.5, 1.OA.C.6]
Grade 2 [2.NBT.5, 2.NBT.B.5, 2.NBT.B.8, 2.NBT.B.9, 2.OA.2, 2.OA.A.1, 2.OA.B.2]
Grade 3 [3.MD.C.5, 3.NBT.2, 3.NF.1, 3.NF.2, 3.NF.3, 3.NF.A.1, 3.OA.1, 3.OA.5, 3.OA.9]
Grade 4 [4-MD.3, 4.MD.1, 4.MD.2, 4.NBT.6, 4.NF.3, 4.NF.5, 4.NF.6, 4.OA.1, 4.OA.5]
Grade 5 [5.B1.7, 5.D1.3, 5.D1.6, 5.MD.1, 5.MD.3, 5.MD.4, 5.MD.5, 5.NBT.2, 5.NBT.3, 5.NBT.6, 5.NBT.7, 5.NF.1, 5.NF.2, 5.NF.3, 5.NF.4, 5.NF.5, 5.OA.1, 5.OA.2, 5.OA.3]
Grade 6 [6.EE.1, 6.EE.2, 6.EE.5, 6.EE.6, 6.EE.7, 6.G.1, 6.G.2, 6.NS.1, 6.NS.3, 6.NS.6, 6.NS.B.3, 6.NS.C.6, 6.NS.C.7, 6.NS.C.8, 6.RP.1, 6.RP.2, 6.RP.3, 6.RP.A.1, 6.RP.A.2, 6.RP.A.3, 6.RP.A.3.C]
Grade 7 [7.EE.3, 7.EE.4, 7.EE.A.1, 7.G.3, 7.G.4, 7.G.6, 7.NS.A.1, 7.NS.A.2, 7.RP.1, 7.RP.3, 7.RP.A.2.B, 7.RP.A.3, 7.SP.2, 7.SP.5, 7.SP.6]
Grade 8 [8.EE.1, 8.EE.5, 8.EE.6, 8.EE.7, 8.EE.8, 8.F.2, 8.F.3, 8.F.4, 8.F.5, 8.G.5, 8.G.6, 8.G.7, 8.G.9, 8.SP.1]
Grade 9Kindergarten [K.CC.A.1, K.NBT.A.1, K.OA.A.1, K.OA.A.2, K.OA.A.3]
Practice [MP.1, MP.2, MP.3, MP.4, MP.6, MP.7]
Statistics & Probability [S-ID.6, S-MD.4]