Last year, our district focused our system wide math content learning on number sense and numeration including counting and quantity principles, composing and decomposing numbers, addition and subtraction as well as multiplication and division while exploring these concepts through a spatial perspective. This school year, we continue to our work in number sense and numeration by deepening our understanding of whole number as well as introducing fractions.

Thus far, much of our work has been grounded in the ideas in the Paying Attention to Fractions document, the recently released Fraction Learning Pathway and some well known books including Uncomplicating Fractions.

Recently, Heidi Horn-Olivito and I were at a Math Knowledge Network meeting in Toronto where we were lucky enough to bump into Beverly Caswell, co-author of Taking Shape. Heidi and I were planning a task for an Uncomplicating Fractions book talk and Beverly was kind enough to help us out during the brainstorming process. As a group, we came up with some great ideas and here’s how it might look in different classrooms.

A Possible Kindergarten to Grade 4 Approach

Before this lesson, you will want to print and cut out the following materials:

You can DOWNLOAD THE TEMPLATE FILES HERE.

Act 1: Spark Curiosity

Hold up the small square and the big square and ask them:

What do you notice? What do you wonder?

After allowing students some time to generate some things they notice and some wonderings, allow them to share with their neighbours. Finally, select some students to share with the entire group.

As usual, we will acknowledge all that the students share.

Act 2 – Give Some Information

Our first wonder we will go with is:

How many small squares do you think it will take to cover the big square?

Act 3 – See If It Works!

Since my 5-year-old daughter Taliah found this activity in my bag, I figured I’d try it out on her and her 3-year-old brother, Landon.

Here’s a video of what they did.

I was actually really impressed with how Taliah used her spatial reasoning skills to determine how many of the small squares she needed to cover the big square!

Fuel Sense Making!

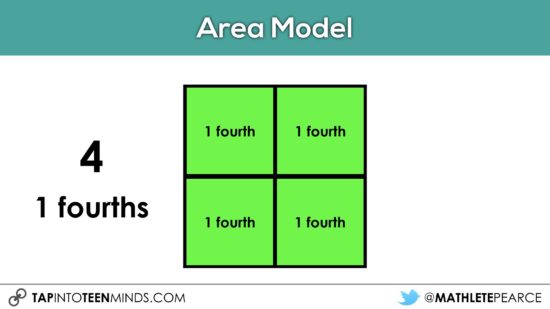
At this point, it might be useful to consolidate with students that the 4 small squares required to cover the big square can be considered 4 parts of the whole. These 4 parts can be called “fourths”. While we might use the word “quarters” when referring to fourths quite often, I would suggest holding off on that word at least for now.

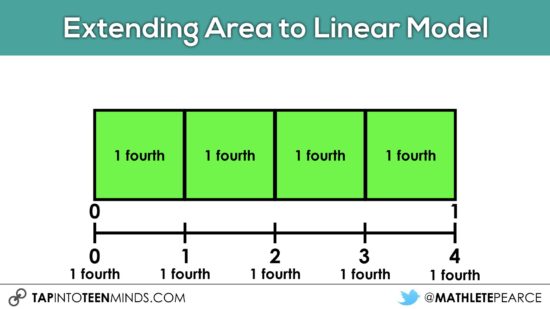
If your students have had exposure to whole numbers on a number line, then this could be a great spot to relate the area model we are working with to a linear model using a number line.

You will notice that I have intentionally avoided the use of standard notation (i.e.: 1/4, 2/4) of a fraction to highlight the unit fraction of “1 fourth”. You can read more about the importance of the unit fraction through the work of Cathy Bruce and the Fraction Learning Pathway. Helping students understand that when we are working with fractions, we are counting a certain “unit” or equal partition of the whole. In this case, we are counting fourths as “0 one fourths, 1 one fourths, 2 one fourths, 3 one fourths, …” and so on. If students can recognize early on that they are counting fractional pieces in the same manner they would count candies, cheerios, or books, it would seem logical that they could better connect the idea of fractions as simply a unit of measure.

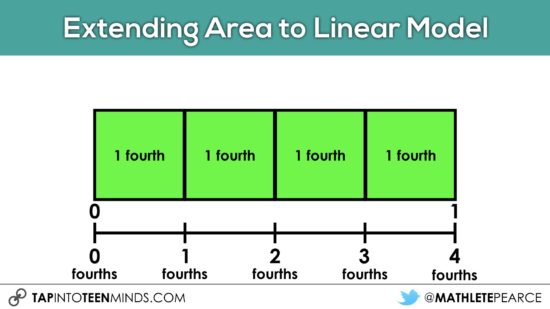
Over time, you might gradually move from a unit of “one fourth” to “fourths”:

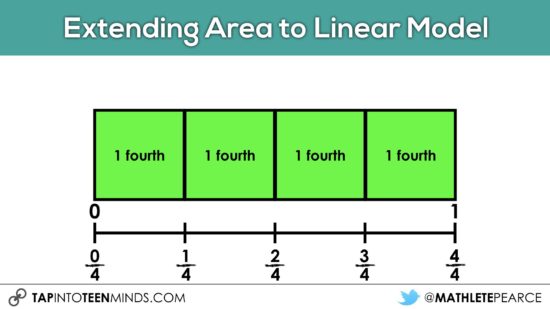
And when students are ready, we can make a smooth transition from writing the unit in words to standard fraction notation.

In Ontario, this transition happens in Grade 4.

Task #2 – Partitioning into Triangles

Next, I asked the same question, but this time with triangular pieces that are half the size of the small squares:

How many triangles would it take to cover the big square?

Here’s a video of what Landon did initially.

So, not quite what I was hoping for, but he did manage to cover the entire square using a combination of 4 triangles and 1 square. I thought that was pretty telling as to the spatial reasoning he was using in order to cover up the whole.

And, as children often do when another is receiving attention, Taliah copied his design initially.

However, as you’ll see in this video, Taliah determined the number of triangles it would take to cover the square by only placing 1 on the big square. She then visualized how many other pieces she would need coming up with an answer of 8.

I attempted to help her make the connection that 4 pieces of a whole are called “fourths” and 8 pieces of a whole are called “eighths”, but when she bumped her triangles off the square, her attention was lost. Will have to try to come back to this in one of the later activities.

Task #3 – Partitioning into Smaller Squares

Although I’m not set on a specific order of the next few tasks, I thought that sticking with a smaller square would be best for them despite there being more partitions (16 total).

So, the question now is:

How many of the really small orange squares will it take to cover the big white square?

Here’s a video of what Taliah and Landon did.

As you saw in the video, Taliah again used only one of the parts to determine how many it would take to cover the whole.

We even managed to make the connection between a whole partitioned into 4 parts being called “fourths” and when we partition the whole into 16 parts, we call them “sixteenths”. You may have also caught her say a “oneth” – referencing what I assume was the big white square. Makes me wonder whether we want to maybe use a bit of slang calling wholes “oneths” and halves as “twoths” (prounounced “tooths”). Worth thinking about, I think.

I then asked her to prove it by handing her a big pile of small squares (sixteenths).

Something worth noting is that in the Ontario curriculum is the fractional pieces students are expected to work with in each grade level.

For example, the specific partitioning mentioned in the following grades are as follows:

• Grade 1 – halves; fourths or quarters
• Grade 2 – halves; fourths or quarters; eighths
• Grade 3 – halves; thirds; fourths or quarters;
  *specifying the use of more than one fractional piece (e.g.: one half; three thirds; two fourths or two quarters) without using numbers in standard fractional notation
• Grade 4 – halves; thirds; fourths or quarters; fifths; tenths;
  *specifying the use of standard notation and the use of the word denominator to represent the number of partitions of the whole for the first time in the curriculum
• Grade 5 – denominators of 2, 4, 5, 10, 20, 25, 50, and 100
• Grade 6 – denominators of 2, 4, 5, 10, 20, 25, 50, and 100

In Grade 7 and 8 there are no explicit references to which denominators should be used, which suggest that students should be working to become flexible with any denominator.

With this said, by no means does the curriculum suggest that we hold students back from pressing their thinking. For example, while my daughter is not expected to work with sixteenths for quite some time, it is to my advantage as a teacher to press her for understanding when she is ready. I can certainly assess her on her progress based on her own learning needs, but should not formally evaluate her via a mark, grade or report card on this specific learning.

Task #4 – Partitioning into Small Rectangles

Interestingly enough, when I gave Taliah the whole partitioned into rectangular pieces, her visualization / spatial reasoning skills let her down.

She initially believes that it will take 16 to cover the white square. So, I toss a pile of blue rectangles at her and let her get to work. Here’s a video showing what she came up with.

I thought this task was a great example of how important concrete materials come into play when we are discovering new ideas in mathematics. Taliah was using her visualization skills to help guide her thinking earlier. Now that the number of partitions are increasing and the shape of the partitions are becoming more difficult to visualize for her, she is forced to go back to the concrete manipulative (cutouts of the shapes) in order to guide her thinking.

Fuel Sense Making: What Happens to the Name When The Whole Changes?

It would be really easy for me to walk away from this task thinking my kids have done some great work with fractions (and I think I’d be right). However, we are constantly leaving money on the table in our classrooms and I almost left some here in this case.

Next, I wanted to see if Taliah was thinking in absolute or relative terms. If she was thinking in absolute terms, she might believe that the green squares were ALWAYS fourths and the small orange squares were ALWAYS sixteenths. If she is thinking in relative terms, then she would know that the name of each piece would change based on what we were comparing it to. This is super heavy, so I wasn’t really expecting much.

Boy, was I wrong. Check out the video here.

As you see in the video, she seems to be able to think in relative terms. Something that is so important for students as they develop their fractional, multiplicative and proportional reasoning skills over the next handful of years.

Student Samples Submitted

Check out all of the great samples of student thinking shared from around the web! Keep them coming!

First, Lisa Burke submitted a video of her son, Henry engaging in some pretty awesome fractional thinking:

Then, we had Ms. Cruickshank from John Campbell Public School submit a great video series of student thinking. Definitely worth the 9 minute watch:

Thanks to everyone for submitting student work samples. Would love to see more!

What About The Older Grades?

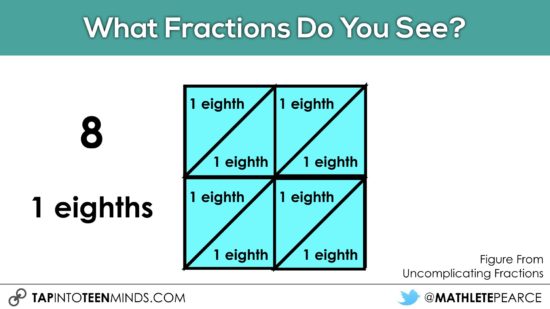
I find that teachers in junior and intermediate grades tend to want something a bit more “robust” and they might consider jumping straight to this image grabbed from Marian Small’s Uncomplicating Fractions book:

Many teachers I’ve worked with have found that students actually struggle quite a bit with this problem. Often times, what students miss in this particular visual is to define the whole. Some students will see the entire “big” square as the whole, while others might look at each fourth of the big square as a whole.

The good part is that as long as the student clearly articulates the whole they are referring to, the name of their fractional pieces can be different than another student in the class.

For example, if one student says the rectangular pieces are “thirds”, then they should also be able to articulate that we can visually see 4 wholes since you could fit 12 thirds over the entire image.

As you can imagine, playing with the idea of comparing fractions and equivalent fractions could easily be tied in as well as extending to operating on fractions.

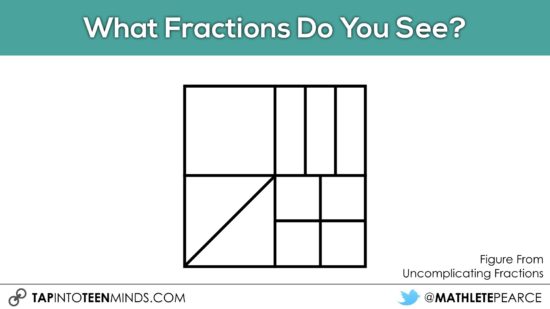
Some other interesting visuals to use and address such as:

Even in older grades, it would be worth giving students the cut out of this visual so students can predict and then prove by folding and/or cutting. They’ll find out in different ways that each partition is a fourth.

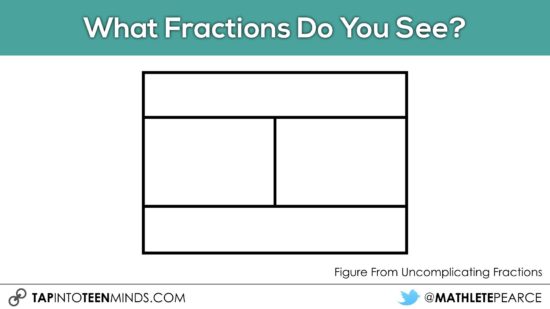
Here is another to consider using:

Thinking about using this task in your classroom? Download the printable PDF below:

Would love to hear how you use these tasks in your classroom. Let us know in the comments!