Division From Fair Sharing to Long Division and Beyond
Over the past school year, I have had an opportunity to work with a great number of K to 8 teachers in my district with a focus on number sense and numeration. As a secondary math teacher turned K-12 math consultant, I’ve had to spend a significant amount of time tearing apart key number sense topics including the operations. While I often hear teachers concerned about multiplication skills of their students, an operation that doesn’t come up too often in discussion is division. However, what I found interesting this year was how much of a struggle it was for teachers to attempt representing division from a conceptual standpoint instead of simply relying on a procedure. After spending quite some time diving into division independently as well as collaboratively with educators through workshops, I will attempt to share what I believe to be some pretty important pieces along the progression of division.
Disclaimer:
This is by no means a complete progression and would welcome other pieces in the comments that I could add in to build on this post over time. I have found thinking about these pieces as pivotal in my own understanding of how division is constructed over time, but will likely continue changing as my own understanding deepens.
I would recommend first exploring the progression of multiplication prior to jumping into this post focusing on the opposite operation, division.
Unitizing: Creating Groups
Before we begin diving into division, I feel it is important for students to be very efficient with unitizing which I discuss in a separate post with counting principles.
To summarize, unitizing is:
Understanding that every quantity we measure is relative to another pre-measured group we call a unit. For example, our base ten place value system.
Before students can successfully unitize, they must be able to count via one-to-one correspondence. For example, a student successfully counting a group of items, one at a time.

After learning one-to-one correspondence and working on other principles of counting and quantity, teachers can begin encouraging students to skip count by 2s, 3s, and so on. This might be considered the beginnings of having students unitize implicitly. For example, by counting by 2s: 2, 4, 6, 8, and so on, students are counting up by a group larger than 1. Over time, students can begin counting the groups of 2 (or whatever unit they are skip counting by) with their fingers to really bring out unitizing explicitly.


Once students are able to count groups of 10, they are not only well on their way down the progression of division, but also on their journey to conceptually understanding our base ten place value system.

Creating Equal Groups By Fair Sharing
Something that comes quite natural to young children is the ability to fair share a group of items. For example, sharing a handful of candies between siblings isn’t something that is typically taught explicitly, but rather students develop this sense of fairness through play.
Prior to attempting to formalize division as an operator, students should have extensive experience fair sharing items amongst friends, both concretely (by sharing to real people like their classroom peers) and when ready, visually/pictorially (by sharing to groups organized on their desk, on paper or on a whiteboard).
An example of such fair sharing is given in the Ontario Grade 2 Mathematics Curriculum in the Number Sense and Numeration strand:
represent and explain, through investigation using concrete materials and drawings, division as the sharing of a quantity equally (e.g., “I can share 12 carrot sticks equally among 4 friends by giving each person 3 carrot sticks.”);

As students become more comfortable with the idea of fair sharing, they may begin unitizing the amount of carrots that they share fairly. For example, in this same situation, an experienced student may notice the large group of carrots and begin to share two carrots at a time. You can understand why skip counting backwards can be helpful in completing this task.

Formalizing Division As An Operation
Once students are comfortable with fair sharing using repeated subtraction in units of 1 or more, we can begin formalizing this idea as an operation we call division.
In the Ontario curriculum, we begin formalizing division in Grade 3 using tools and strategies up to 49 ÷ 7:


Two Types of Division: Partitive and Quotative
Something that is not stated explicitly in the Ontario mathematics curriculum and can easily be overlooked by elementary math teachers is that there are two types of division: partitive and quotative.
Partitive Division
Also Known As Fair Share or Sharing Division
The first type of division we will explore is called partitive division. This type of division is possibly the first type of division students intuitively experience when they are young by sharing a group of items with their friends as we did earlier by sharing 12 carrots amongst 4 friends. In other words, partitive division occurs when a scenario requires a student to divide a set of items into a given number of groups, where the number of items in each group is unknown.
To give another example, we could look to the following question from Alex Lawson’s book, What to Look For, where a student is asked to answer the following question:
You buy 15 goldfish. You are going to put them in 5 jars evenly. How many goldfish will you put in each jar?


After viewing the visualization above of the student distributing the goldfish by assigning one fish to each bowl at a time, it becomes more obvious as to why we also call partitive division “fair sharing”.
Quotative Division
Also Known As Subtraction or Measurement Division
The second type of division we will explore is commonly known as quotative division. This type of division occurs when a scenario requires a student to divide a set of items into groups with a given amount in each group, where the number of groups is unknown.
To rearrange the previous question as an example of quotative, we might ask the student this question:
You buy 15 goldfish. You are going to put them in jars, with 3 in each jar. How many jars will you need?

Since a quotative division problem tells the student how many items should be in each group, it would seem reasonable to assume that the student would unitize the 15 goldfish into units of 3 until all of the goldfish have been used and then count the number of groups created. When a student completes this problem, possibly using cubes or square tiles to represent each of the goldfish, they are implicitly using repeated subtraction to take away 3 goldfish at a time from the total of 15.

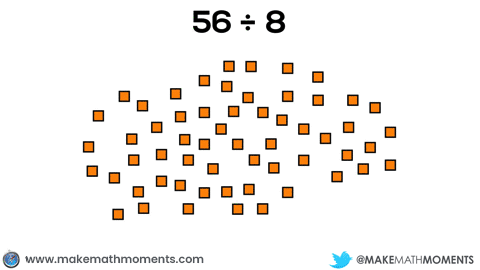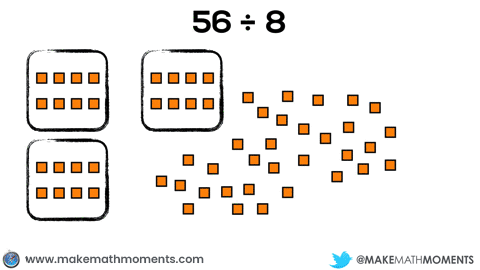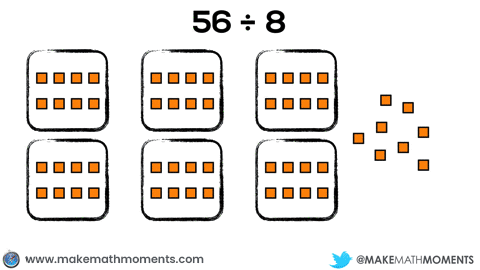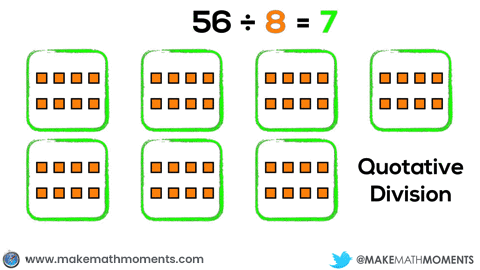
The visualization here shows the student measuring groups of 3 fish and then repeatedly subtracting those groups from the set of 15 fish until there are none left. Hence the names “measured” and “subtracting” division.
Summarizing Partitive and Quotative Division
In summary:
Partitive Division
- Number of groups is known; and,
- Number in each group is unknown.
Quotative Division
- Number in each group is known; and,
- Number of groups is unknown.

While I personally am less concerned about teachers being able to name these two types as quotative and partitive, it is important that teachers are aware that two types exist to ensure that they are exposing their students to contexts that address both of these types.
Examples of Partitive and Quotative Without Context
When using division without context like fair sharing carrots or placing goldfish in jars evenly, the student can decide whether to use a partitive or quotative strategy based on what they are most comfortable with. While convenient, a potential pitfall may arise if students divide procedurally using only one type of division while ignorant to the fact that another type of division exists.
For example, if a student were to model 56 ÷ 8 using square tiles, a student could approach this using partitive division by fair sharing the 56 tiles evenly into 8 groups like this:
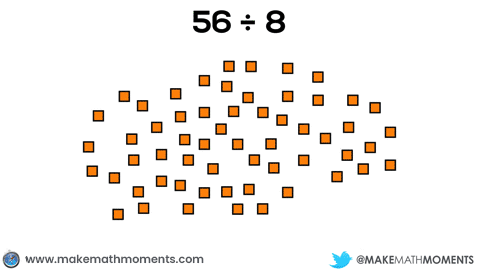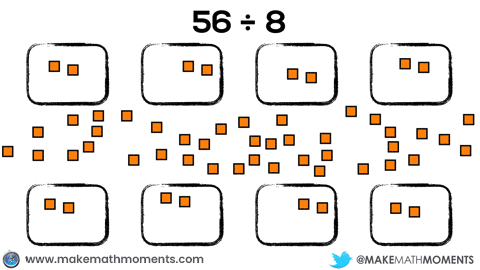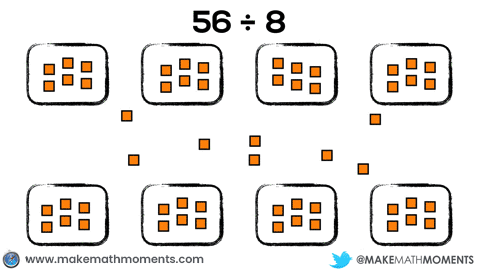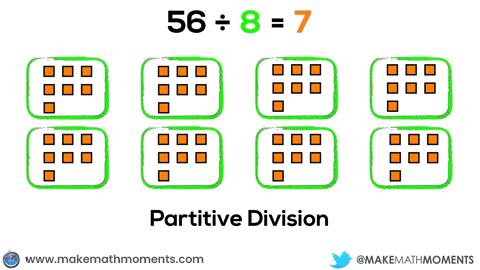
Or, the student could choose to model this problem by using quotation division by repeatedly measuring out groups of 8 and subtracting them from the set of 56:
Division With Arrays: Moving From Equal Group “Piles” to Rows and Columns
You’ll probably notice that regardless of which type of division students are using, they often make circular piles of the item they are working with. I believe this to be an important stage in the progression as it seems fairly intuitive to simply create your groups without ordering or organizing the items in each group.
As the dividends and divisors that students work with get larger, it can be helpful to think about organizing the items to help promote unitizing as well as building conceptual understanding and procedural fluency of division using arrays.
For example, if we look at an extreme case of dividing 120 ÷ 8 using individual square tiles, we can still identify partitive and quotative division:

While I don’t want students spending too much time trying to divide large dividends using square tiles, it could assist in showing students why base ten blocks are helpful.
Just like with multiplication, I think students should have a significant amount of experience dividing with arrays up to 81 ÷ 9 if you hope to help them conceptually understand division with dividends greater than 100.
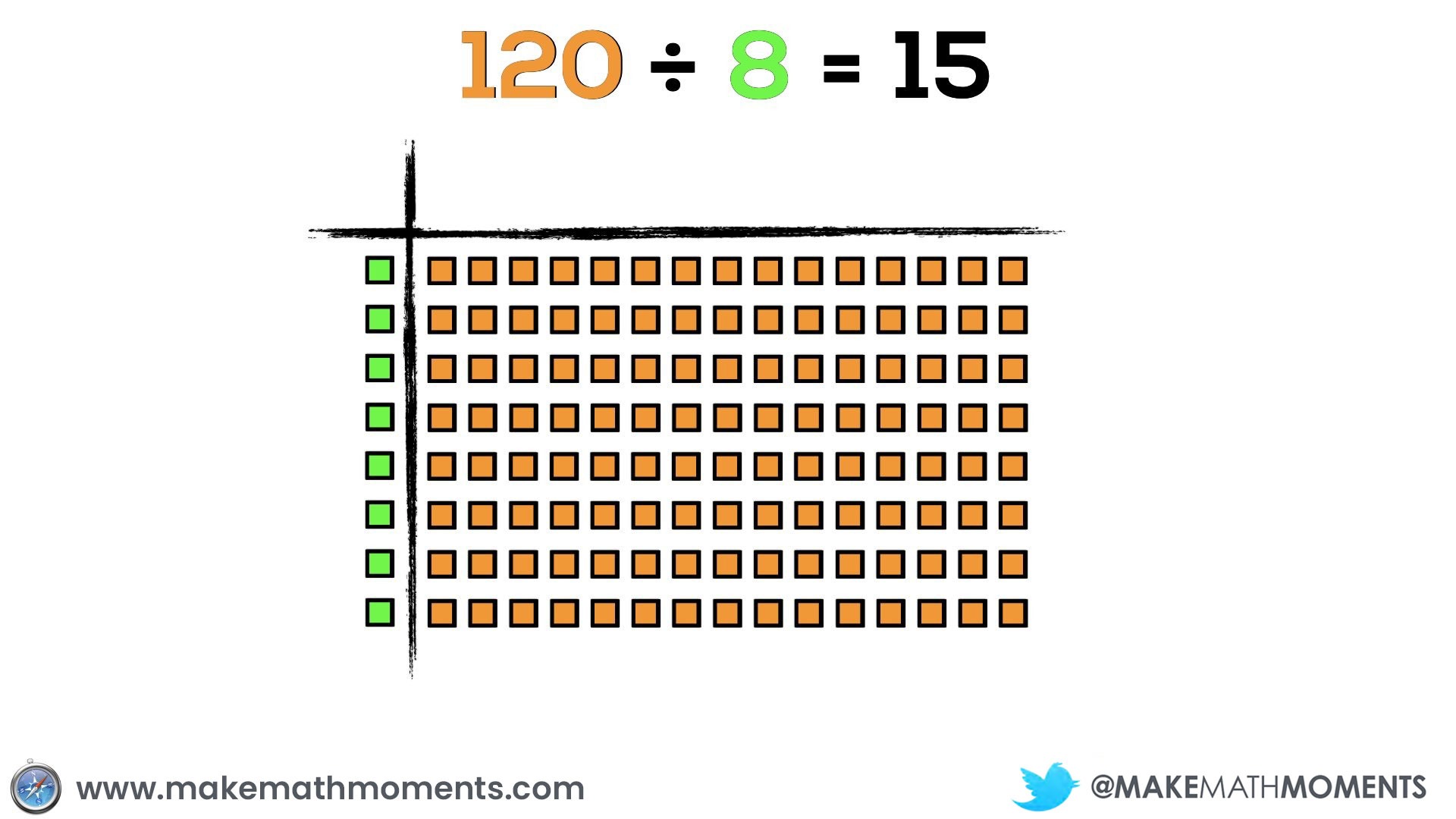
Not sure what is going on in the above image? Be sure to check out the progression of multiplication before going on where we explicitly address arrays and area models which we will be diving into pretty quickly here.
Division With Large Arrays: Base Ten Blocks
It doesn’t take long for students to become annoyed by trying to use square tiles to represent division with large dividends. Thankfully, as we saw in our Progression of Multiplication post, we can turn to base ten blocks to cut the hassle.
For example, if a student wants to model 120 ÷ 12, they could use 1 hundred flat and 2 ten rods to represent 120 and 1 ten rod and 2 units to represent 12. The representation would be similar to multiplication, except in this case, you have one factor (12) and the result (120) and you must find the unknown factor:
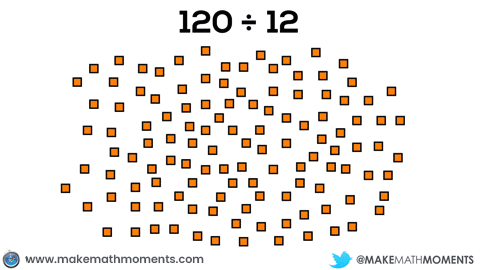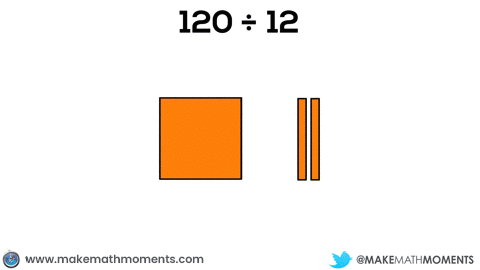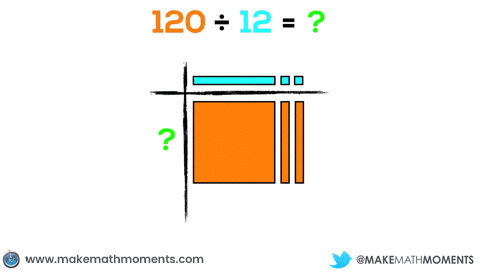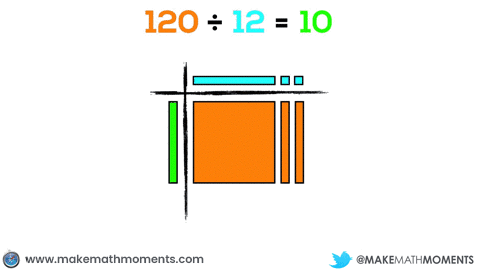
It is easy to see the benefit of using base ten blocks when dividends get large. Instead of using 120 individual square tiles, we can use 3 base ten blocks to represent the same dividend. I intentionally selected a fairly easy example to begin with in order to allow students the opportunity to become familiar with dividing with concrete materials. While it might not seem obvious at first, dividing becomes increasingly difficult when more challenging examples are attempted.
Let’s try another example like 112 ÷ 8.
Your dividend will consist of 1 hundred flat, 1 ten rod, and 2 units, while your divisor consists of 8 units.
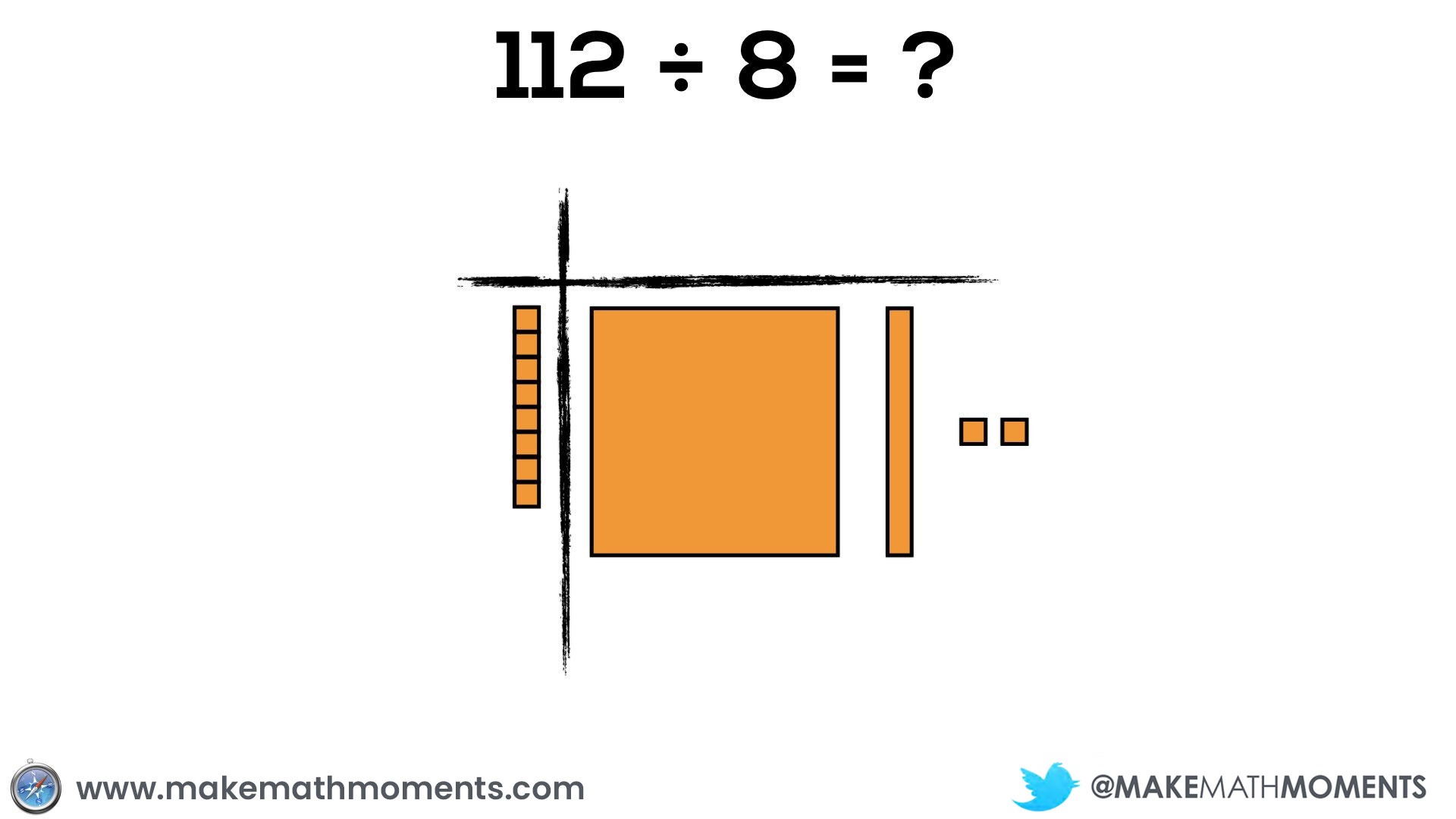
This experience might look something like this:
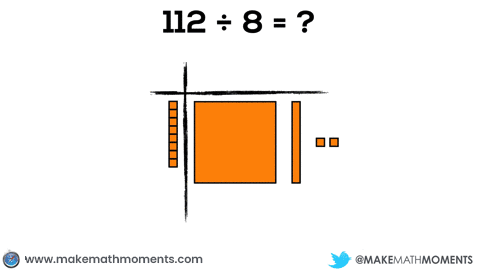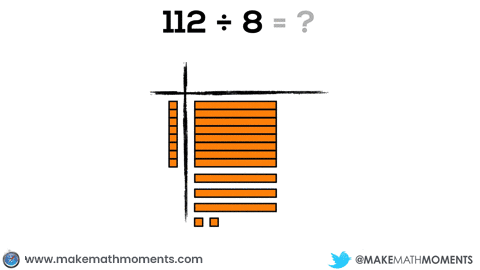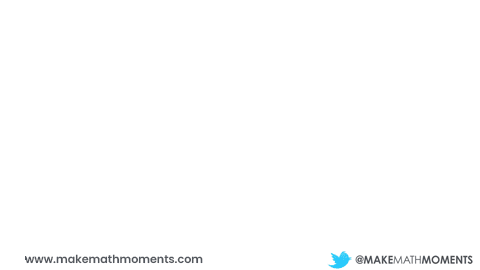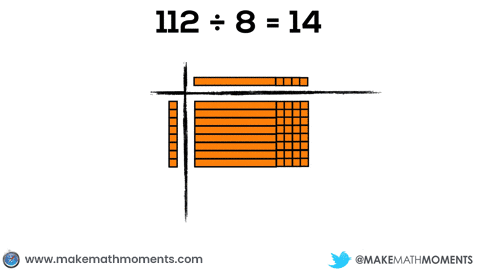
While I will attempt to be as clear as possible in this post, it is important to note that students will need a significant amount of experience at each stage of the progression. Do not attempt to rush or you will find both you and your students frustrated.
Moving From Concrete to Digital Manipulatives
Due to a shortage of concrete base ten materials or to make life a bit easier, students may begin gravitating to digital base ten block manipulatives. While it might seem easier to just jump straight to digital manipulatives, I don’t recommend rushing to this stage as students should really have the opportunity to physically manipulate the base ten materials prior to moving to a digital alternative.
When students have had significant experience manipulating physical base ten materials, you might consider using the Number Pieces iOS app or the web-based version from Math Learning Center.
While using a digital manipulative can be more efficient for a student who is experienced using physical base ten blocks to model division with 3 or more digit dividends, it can be a huge hinderance for students who have not been given an opportunity to build their conceptual understanding in this area.
Division With Base Ten Blocks: Increasing The Difficulty
When I deliver workshops specific to the progression of division, I find teachers quickly jump to the conclusion that dividing with base ten blocks is simply too difficult and unnecessary.
However, I believe quite the opposite.
I agree that using base ten blocks is definitely not the most efficient method a student should use when trying to divide two numbers, but they are very useful for building a conceptual understanding of division as well as a unique opportunity to build strategic competence by problem solving their way to a solution. Less obvious is the experience students are gaining around conversions when they trade in a hundred flat for 10 ten rods, a ten rod for 10 units as well as implicitly building the foundation for factoring quadratics – a grade 10 concept here in Ontario – all the way down in grade 5.
Let’s check out another example: 189 ÷ 9
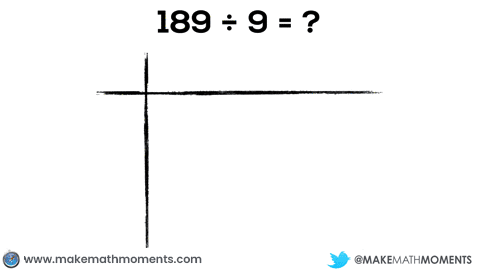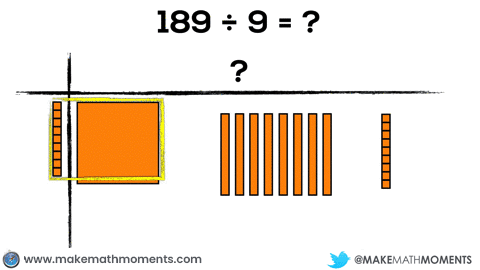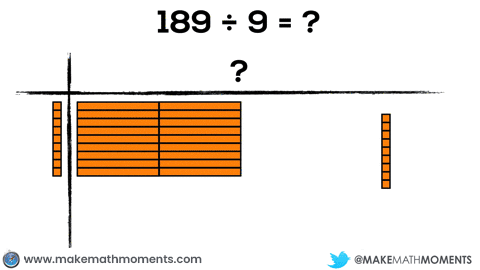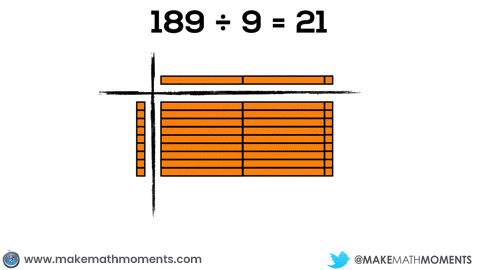
Check out the conversions from hundreds, to tens, to units.
We could go ahead and rush to the long division algorithm, but why would we want to rob students of the opportunity to look at mathematics as a puzzle waiting to be solved?
Still want more practice?
Try 221 ÷ 13 using base ten blocks or Number Pieces app.
Once you’re done, see if your result looks something like this.
Connecting Arrays to Area Models: Distributive Property
Like anything we do in mathematics to build conceptual understanding, we don’t want the learning to stop there. Ultimately, we hope that the rich learning experiences we offer our students will begin to solidify by creating procedural fluency and automaticity. The next step on our way to the long division algorithm is the area model. This model is very useful when dividing and helps set us up for a clear connection to the long division algorithm, which is our end goal for this progression.
If we think about the distributive property from our multiplication post, you’ll remember that we could use this property by “splitting the array”. We can do much the same with division and it is convenient to do so by using open area models. In other words, rather than using square tiles or base ten material to represent an array for multiplication or division, we will use a not-to-scale rectangle in its place. A little less precise, but still gives us the same visual that an array can offer leaving our minds to visualize the rest.
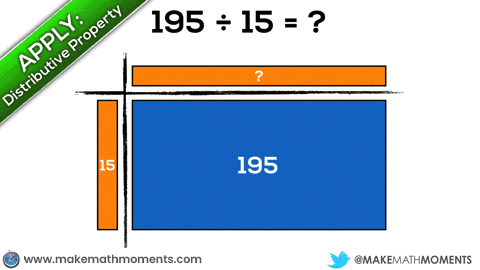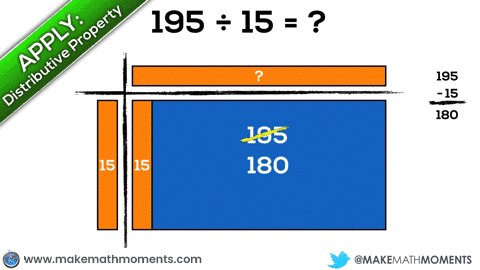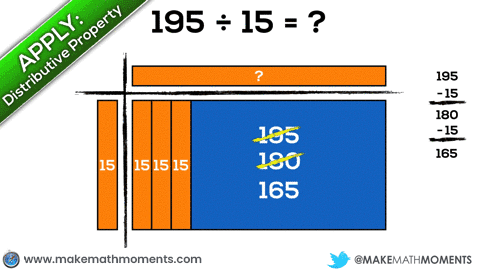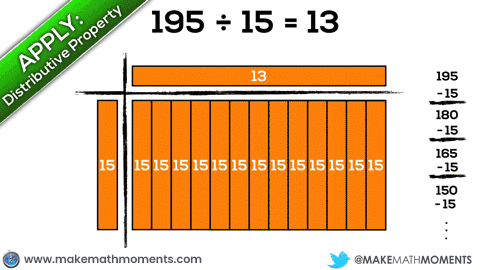
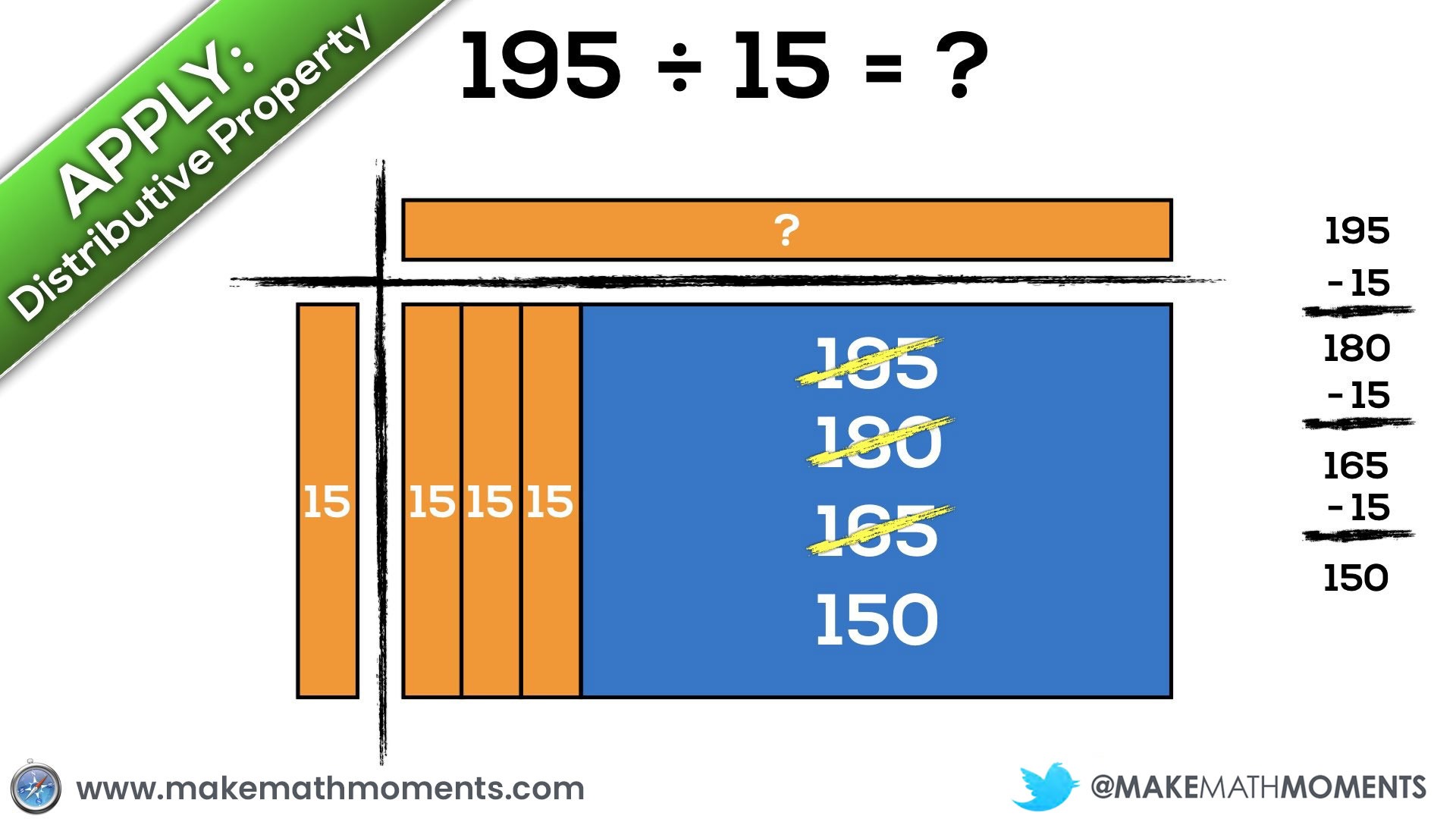
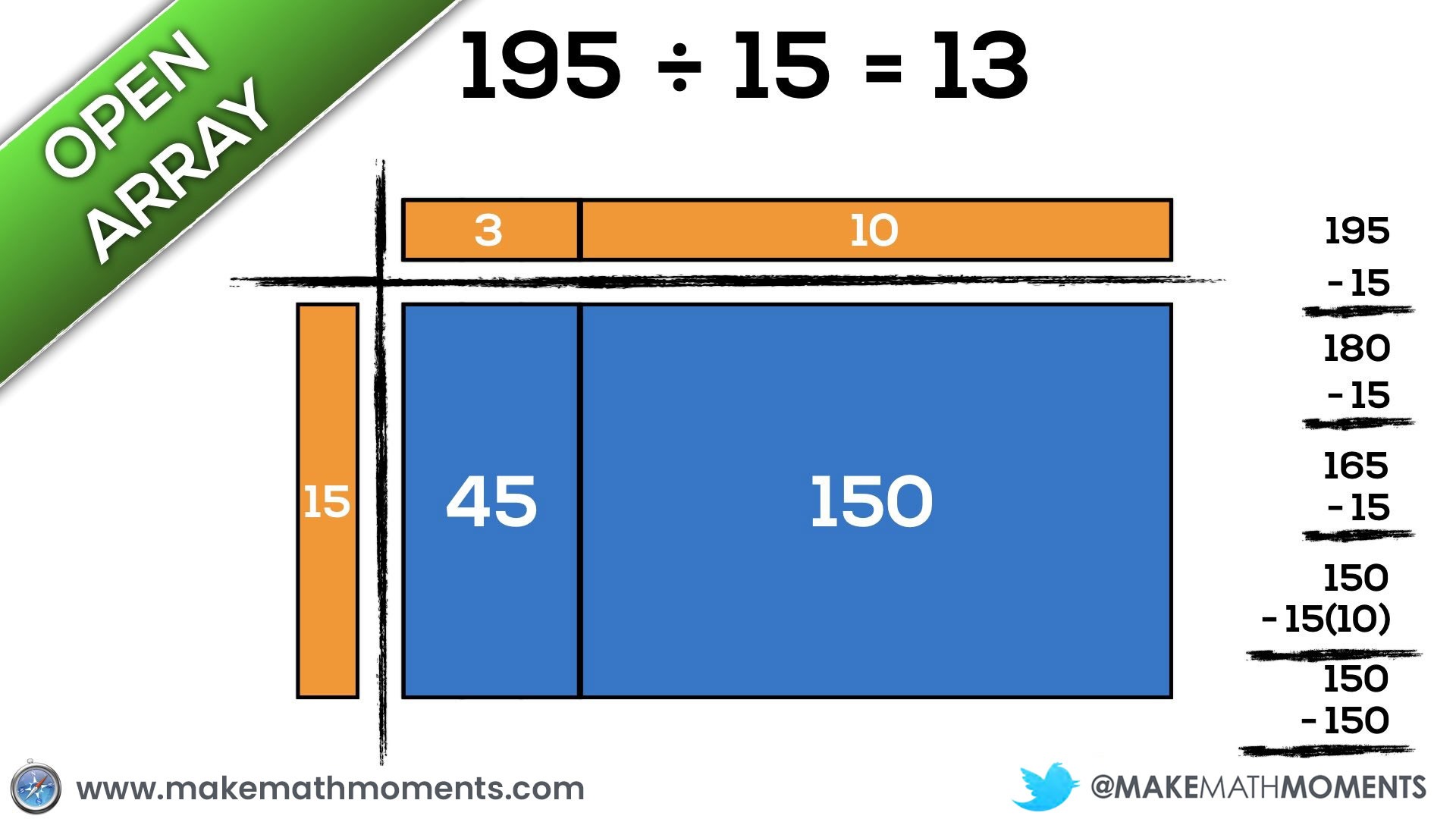
Let’s have a look at 195 ÷ 15 using an area model to represent division.
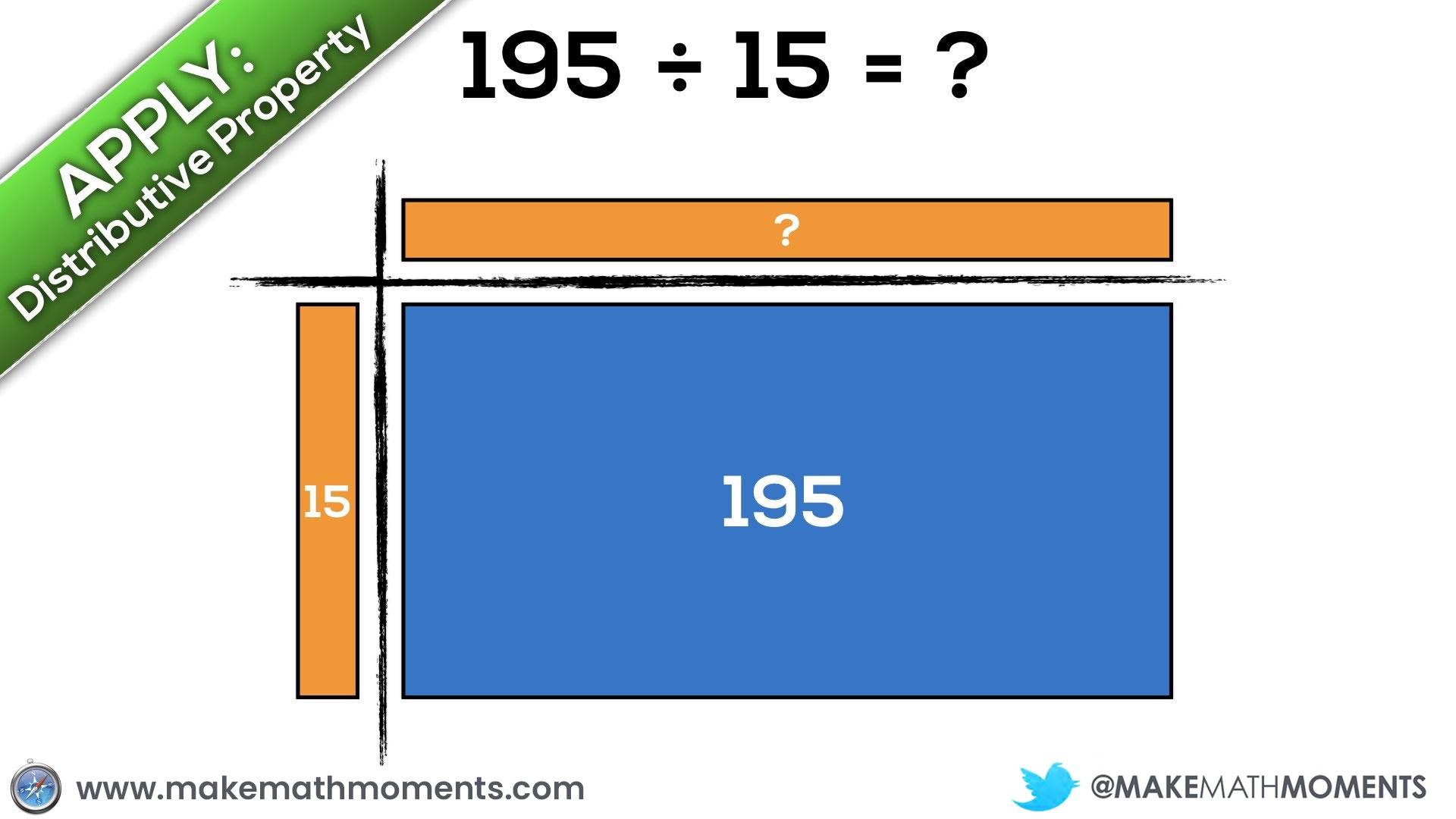
When drawing an area model for division, students are able to essentially unitize their own “chunks” to partitively (divide x items into 15 groups) or quotatively (divide into x groups of 15) approach this division problem.
In this case, I’ll give an example of a student who decides to approach this quotatively by repeatedly subtracting groups of 15 from 195 until running out of items:
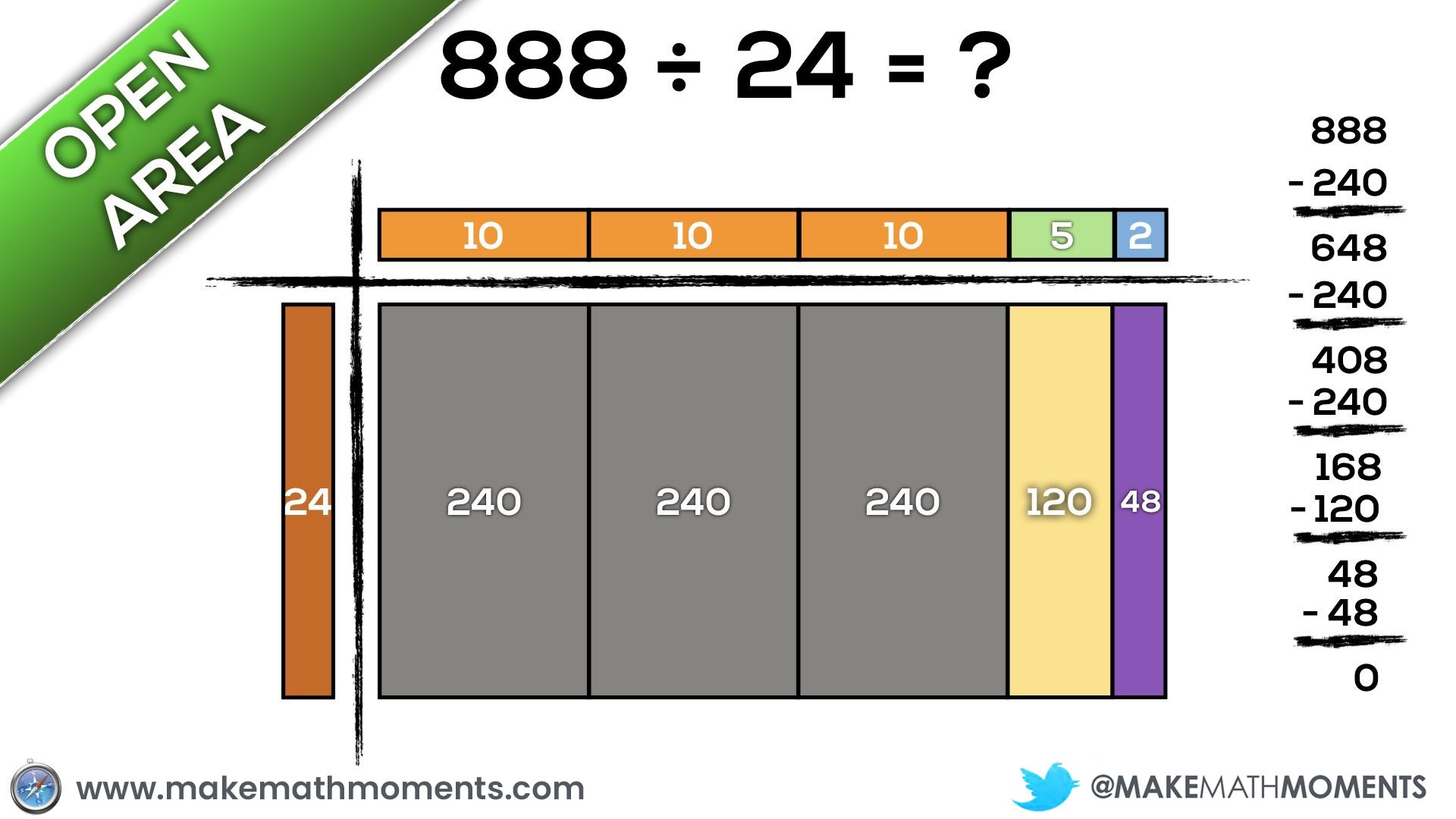
Have a look at a possible approach to solving 888 ÷ 24.
Contextual Division Problems With Open Area Models
While I’m a huge advocate for using context in math class, I’ve kept things fairly contextless for the majority of this post. However, I want to explicitly show that whether there is context or not, these strategies to promote students conceptual understanding and procedural fluency with division are very helpful.
Let’s have a look at a problem with some context involving a pool.
A pool has a width of 14 m and an area of 700 metres-squared.
What is the length?


You may notice that when I’m using area models, I’m using a symbolic approach to keep track of the repeated addition. That method is used in a number of different places with different names. In Ontario, the Guides to Effective Instruction call that strategy “Flexible Division”, since it is very similar to the long division algorithm, but puts the power in the hands of the student to select how many groups of the divisor to subtract with each iteration.
Eventually, students can opt to skip drawing the open area model and using what looks to be the long division algorithm or a variation like flexible division in order to solve division problems without a calculator.
Applying Division With Arrays and Area Models to Factoring in Algebra
As students enter grade 9 and 10, they will be offered an opportunity to put the conceptual understanding and strategic competence they have been developing through division with arrays and area models to use.
When common factoring, students will encounter problems like this one:
A pool has a width of 3 metres and an area of 12 times a number.
What is the length?
It could be helpful for students to create themselves an open area model as we did in the previous example:

When moving from working with multiplication and division to algebra, we rename our concrete materials from base ten blocks to algebra tiles. Instead of units, ten rods and hundred flats, we use very similar tools, but call them units, x-rods and x-squared flats. It should be noted that a hundred flat could also be called a “10-squared” flat.
So, instead of using ten rods like we use with base ten blocks, a student may opt to draw in “x-rods” representing the missing number, x. While there are many ways to approach this problem conceptually, I often see students approaching this additively by adding groups of 3 x-rods until reaching an area of 12 x-rods total. Students might also keep track of their work by using repeated subtraction (or flexible division) to the right of their area model:

Factoring Quadratics With Algebra Tiles Is The Same As Dividing!
Recall our work using base ten blocks and arrays for division earlier in the progression. In our next example, we will look at a similar context using the dimensions and area of a pool to show how all that conceptual work back from grade 5 and 6 can be utilized in Grade 10 to factor both simple and complex trinomial quadratics.
In this example, we’ll explore the following:
A pool has an area of 3x^2 + 11x + 6.
What are the dimensions?
While many students in grade 10 struggle with the idea of factoring quadratics, they may not experience the same level of struggle if they have any experience multiplying and dividing with base ten blocks.
When factoring quadratics, students can simply grab the number of tiles that represent the quadratic they are factoring and then attempt to create a rectangle. Once they find a complete rectangle, they can quickly identify the factors that yield that area. If you can’t make a rectangle, then you know your quadratic cannot be factored with integer coefficients.
Let’s have a look:

Factoring quadratics with algebra tiles is actually much easier than dividing with base ten blocks due to the fact that you are not required to convert from hundred flats to ten rods and ten rods to unit tiles! Who would have thought that grade 5 was tougher than grade 10?
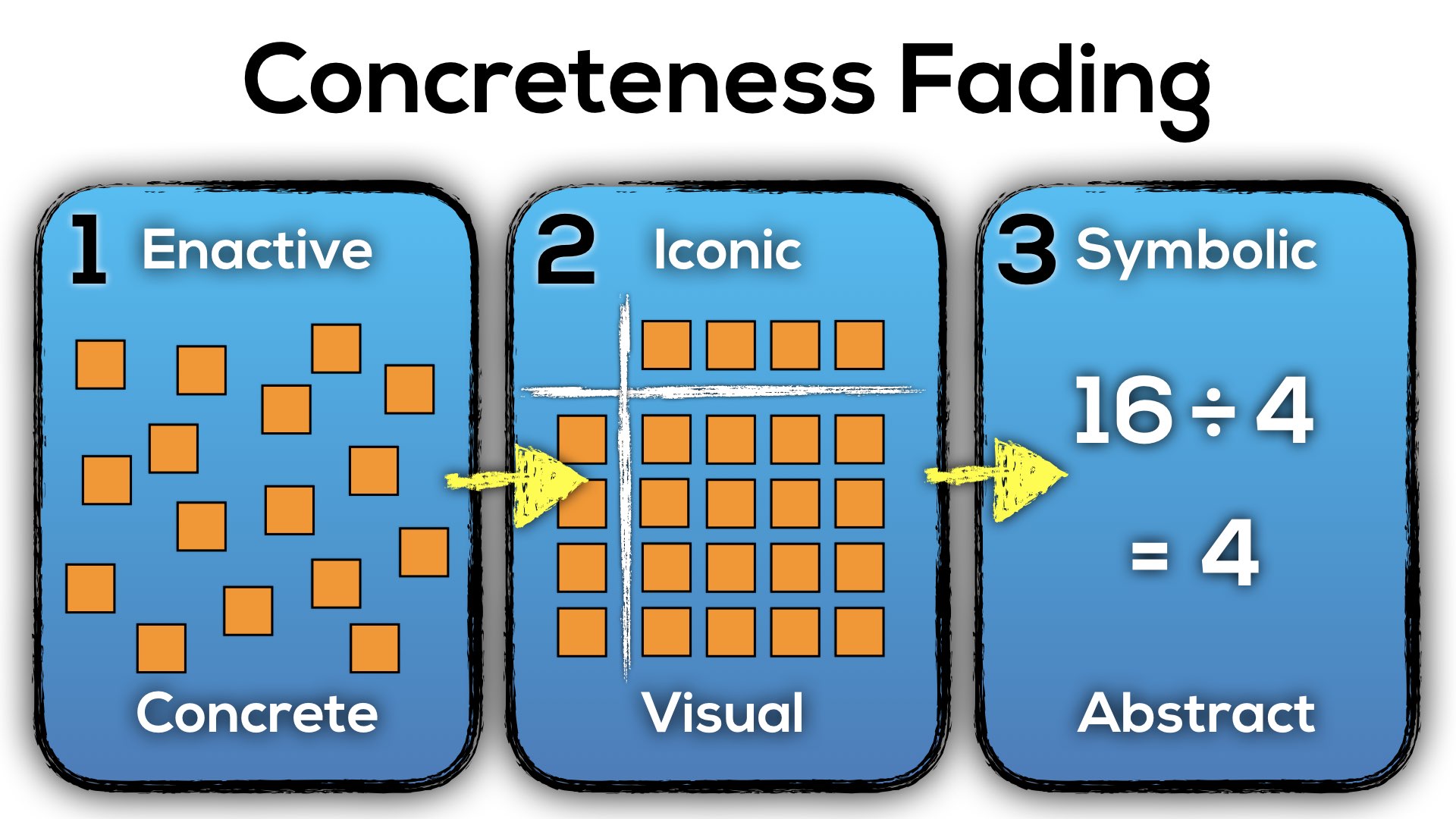
Concreteness Fading: Start Concrete Before Abstract!
As I’ve mentioned in previous posts, there is definitely an argument for starting new ideas in mathematics with concrete manipulatives, slowly moving towards visual (or drawn) representations and finally to abstract representations that use symbols to represent the concrete. Although the name suggests that the concrete stage fades away over time, it is important to note that we should be returning to concrete manipulatives with every new layer of abstraction.
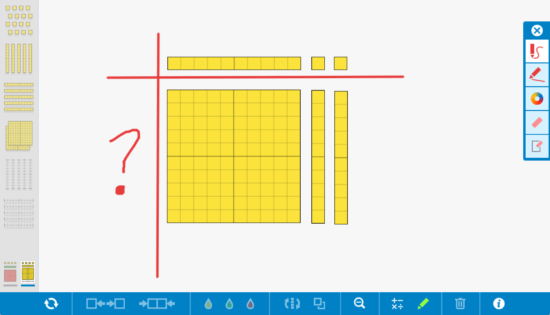
For example, when we first introduce division, we might be working with two digit dividends and single digit divisors. Concreteness fading for this idea might look something like this:
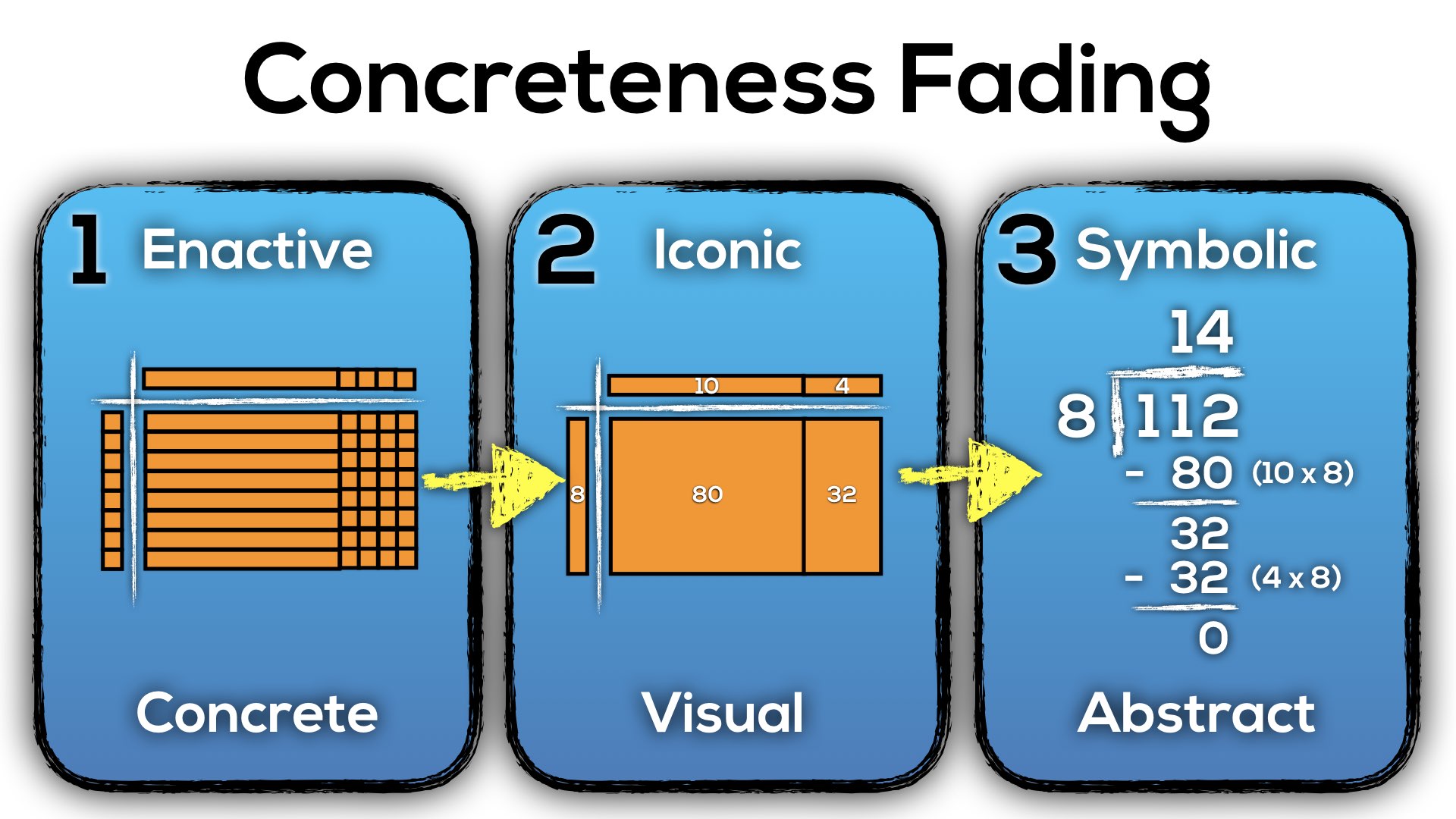
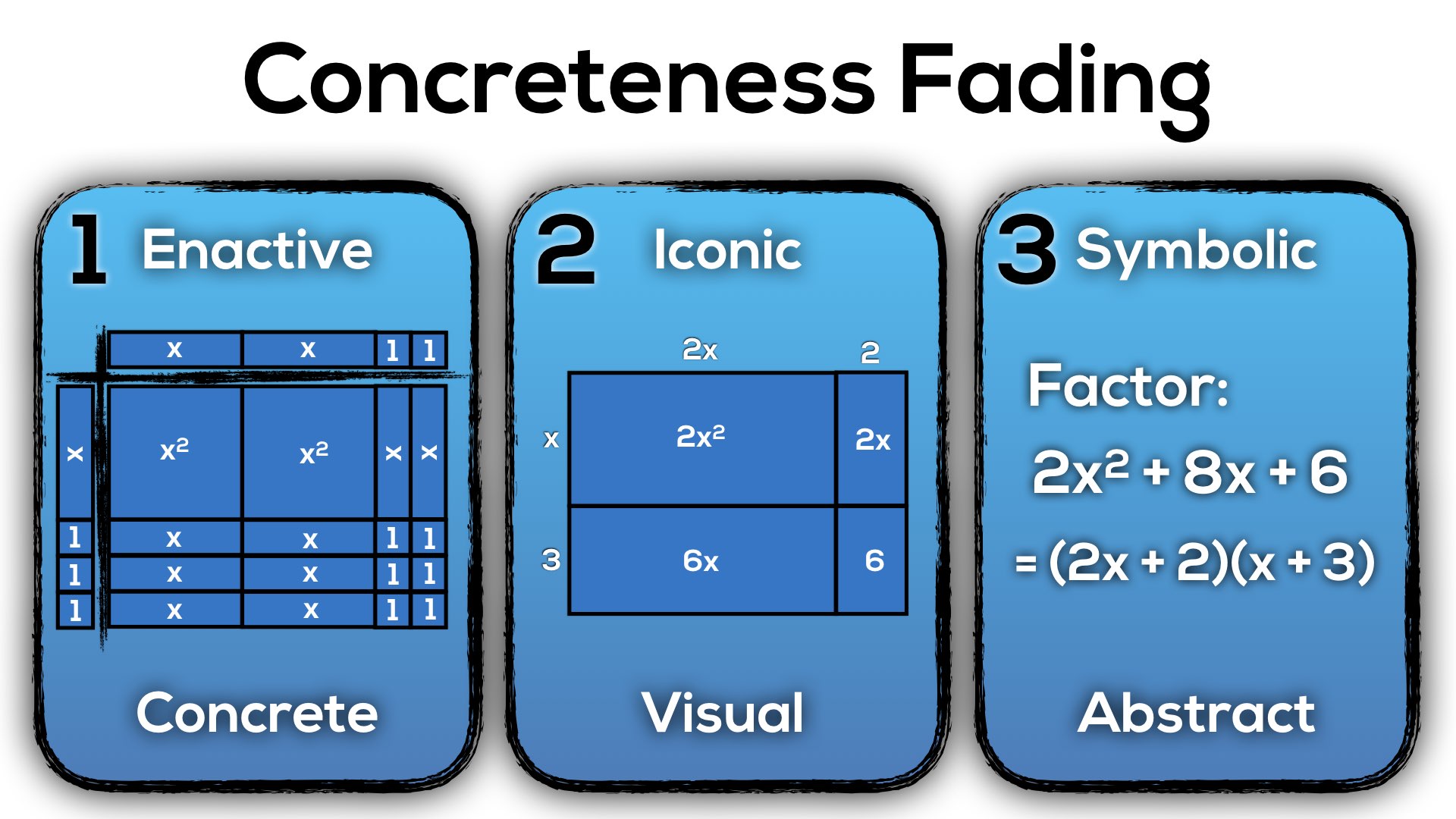
So while this progression of division may not be “the” progression, I certainly hope it shines some light on how important understanding division conceptually through the use of concreteness fading is for promoting the development of a complete understanding for our students.
Interested in checking out some 3 act math tasks that can be used in conjunction with the progression of multiplication and division? Be sure to check out the tasks below:

So … if you could have only one word to express the big idea that unifies all these uses of ‘division’ what would it be?
If it helps, the audience is my 92 year old mother OR a group of adults upgrading their math skills. They want one word they can use to make sense of division.
Division: A Study in …..?….
Great question here…
I might be inclined to say that division is a study of mathematical exploration to build strategic competence and adaptive reasoning. The strategies and mathematical models one can leverage to explore the two types of division and the varying situations can keep you “playing” for years.
This is amazing! Is there a way that I can print this page fully?