Ontario Alignment By Overall Expectation
Grade 2 [Number Sense and Numeration - NS2, Number Sense and Numeration - NS3]
Grade 3 [Number Sense and Numeration - NS3]
Grade 4 [Patterning and Algebra - PA2]
Grade 5 [Patterning and Algebra - PA2]
Grade 6 [Number Sense and Numeration - NS1]
Grade 7 [Patterning and Algebra - PA2]
Grade 8 [Patterning and Algebra - PA2]
MFM1P [Number Sense and Algebra - NA2]
MFM2P [Quadratic Relations in y = ax^2 + bx + c Form - QR3]
MPM1D [Number Sense and Algebra - NA2]
MPM2D [Quadratic Relations - QR4]
From Subitizing and Unitizing to Multiplicative and Algebraic Thinking
This 3 act math task was designed specifically to have a very low floor in order to be useful from primary grades and a high ceiling with an opportunity for many extensions so the task can be used in junior and intermediate classrooms. While I believe this task can touch on many different specific expectations at many different grade levels, listed below are just a few possibilities from the Ontario curriculum.
Regardless of grade level, I recommend teachers show the task videos and and complete the initial “notice / wonder” to spark curiosity. After the initial task is completed, you may decide that jumping ahead to a grade appropriate extension is worthwhile.
Curriculum Connections:
Primary
- Grade 1 – NS1 – estimate the number of objects in a set, and check by counting;
- Grade 1 – NS1 – compose and decompose numbers up to 20 in a variety of ways, using concrete materials;
- Grade 2 – NS2 – compose and decompose two-digit numbers in a variety of ways, using concrete materials;
- Grade 2 – NS3 – solve problems involving the addition and subtraction of whole numbers to 18, using a variety of mental strategies;
- Grade 3 – NS3 – relate multiplication of one-digit numbers and division by one-digit divisors to real life situations, using a variety of tools and strategies;
- Grade 3 – NS3 – multiply to 7 x 7 and divide to 49 ÷ 7, using a variety of mental strategies;
Junior
- Grade 4 – PA2 – identify, through investigation (e.g., by using sets of objects in arrays, by drawing area models), and use the distributive property of multiplication over addition to facilitate computation with whole numbers
- Grade 5 – PA2 – demonstrate, through investigation, an understanding of variables as changing quantities, given equations with letters or other symbols that describe relationships involving simple rates;
- Grade 6 – NS1 – estimate quantities using benchmarks of 10%, 25%, 50%, 75%, and 100%;
Intermediate
- Grade 7 – PA2 – model real-life relationships involving constant rates where the initial condition starts at 0 (e.g., speed, heart rate, billing rate), through investigation using tables of values and graphs;
- Grade 7 – PA2 – evaluate algebraic expressions by substituting natural numbers for the variables;
- Grade 8 – PA2 – evaluate algebraic expressions with up to three terms, by substituting fractions, decimals, and integers for the variables;
- Grade 9 Applied – NA2 – solve first-degree equations with non-fractional coefficients, using a variety of tools;
- Grade 9 Academic – NA2 – solve first-degree equations, including equations with fractional coefficients, using a variety of tools (e.g., computer algebra systems, paper and pencil) and strategies (e.g., the balance analogy, algebraic strategies);
- Grade 10 Applied – QR3 – solve problems involving a quadratic relation by interpreting a given graph or a graph generated with technology from its equation;
- Grade 10 Academic – QR4 – solve problems arising from a realistic situation represented by a graph or an equation of a quadratic relation, with and without the use of technology;
Act 1: Introduce the Task
Show students the act 1 video.
Then ask students to do a rapid write of what they notice and what they wonder.
Students will then share out their noticings and wonderings while I jot their ideas down on the whiteboard.
Some noticings and wonderings that have come up when I’ve used this task include:
- Is that a prop plane or jet plane?
- I noticed the CN Tower in the background, so it is Toronto.
- Is that Billy Bishop Airport in Toronto?
- How fast does the plane have to go in order to get off the runway?
- How long is the runway?
- Where were you flying to?
- Is that the Porter flight to Windsor?
While we may explore some other wonderings, the main question I intend to address is:
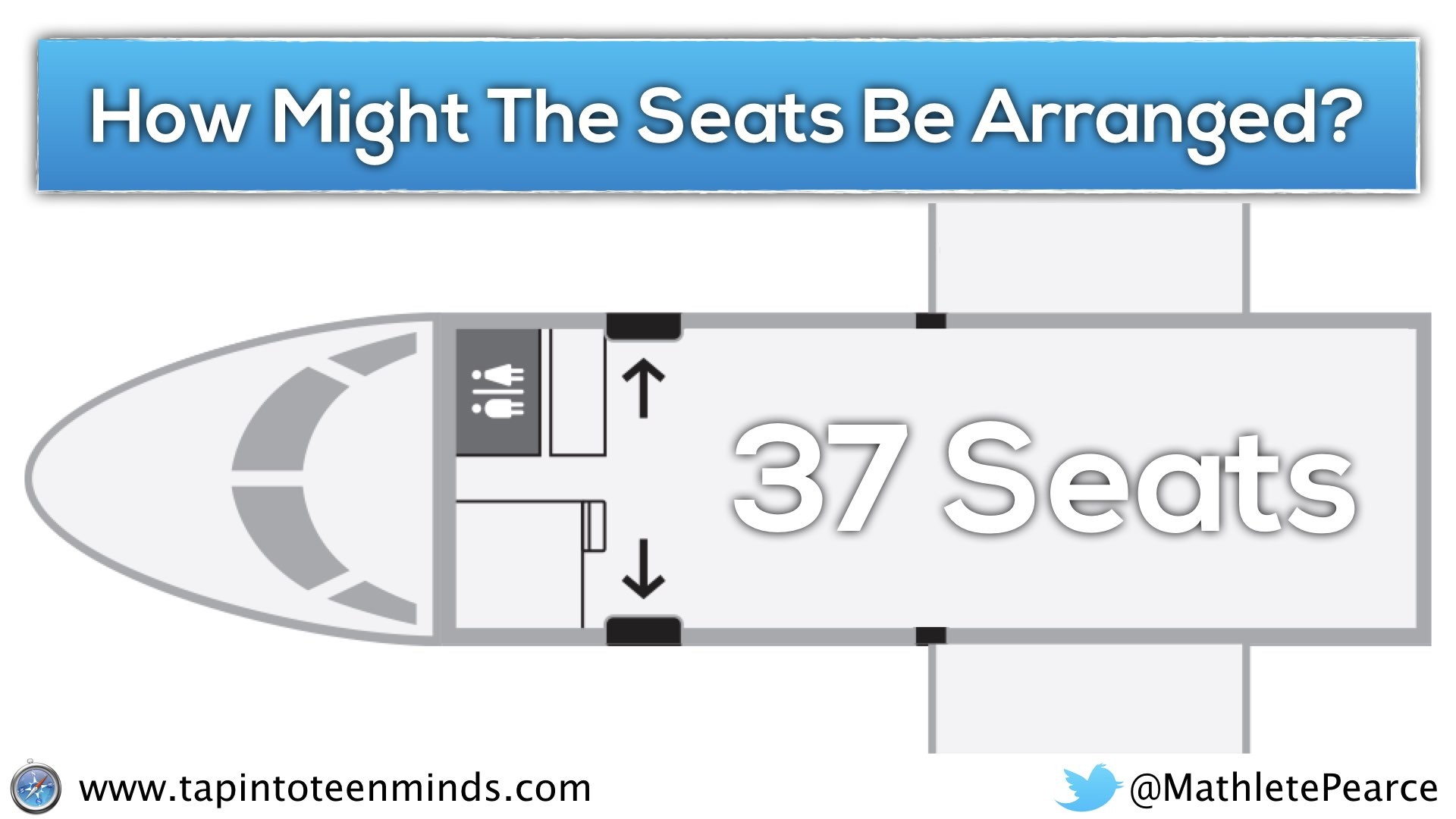
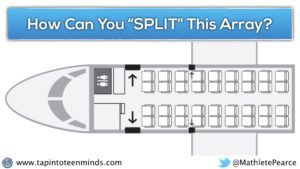
How many seats are on the plane?
With manipulatives already out on their tables, I would then give students some time to make a prediction and discuss with their neighbours and/or group.
Some students may ask clarifying questions like:
- Are we including the pilot(s) and the airplane steward(s)?
- Is the plane up on the screen the actual plane to scale?
- And others…
Airplane Context Not Appropriate For Your Students?
Some folks have mentioned that their students might not have ever travelled on an airplane and/or they are too young to grapple with the context of seats on an airplane.
If you’re struggling with this idea, consider using the following school bus images as the context:
Act 2: Reveal Some Information
After students have shared out their predictions, I would show them this video or this image:
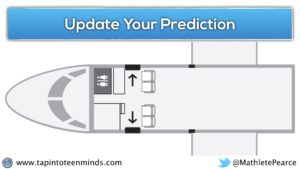
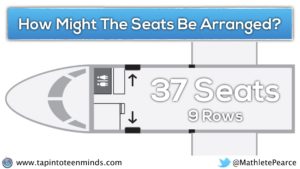
Just a word of caution, that I prefer to reveal the first row only and let them update their prediction. From here, some students might believe that there is a first class/business class section with a different seat size than the remainder of the plane.
Then, I’ll show them the first row and back row with one final update to their prediction before doing the big reveal.
Act 3: Reveal the Solution
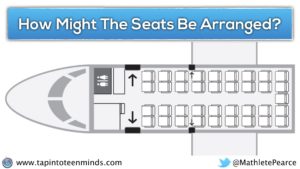
Show students the act 3 video that reveals the total number of seats on the plane:
Alternatively, you can show this image.
Quick Extension
Check out this series of images I recently grabbed on an Air Canada flight that can be useful to keep this context rolling or for coming back to later in the year to put this thinking back on the table. Check them out.
Here’s more to go with those two images:
Alternatively you could ask the question:
Here’s some images to go with that question:
And finally, a few more things you could ask in grade 4 for distributive property and for writing the arrangement of seats using different multiplication sentences:
Deepening the Math Learning
While this is a fun and potentially challenging task for our primary friends, we can easily extend this task to be more mathematically purposeful for our junior and intermediate students. While I wouldn’t skip the portion of the activity we have completed thus far, I do think that we need to dive deeper into the mathematics to strengthen the intentionality of this task.
Let’s have a look.
Encouraging Subitizing and Unitizing
Using an airplane like the one in this task or by going to company websites like Air Canada, you can grab seating plans of different aircrafts to promote counting principles like subitizing and unitizing:
As students begin to unitize, they can begin to start thinking multiplicatively by looking for multiple “groups” of seats to help them skip count and eventually, use multiplication.
Number Sentences and Whole Number Expressions
As students look at an array of seats and head towards thinking multiplicatively rather than additively, we can encourage students to begin applying their ability to compose and decompose numbers with multiplicative thinking.
I love taking a PDF template of the array of seats into GoodNotes 4 on an iPad, SMART Notebook, or any other tech program you use for annotating and lead a number talk to encourage students to share different ways to compose and decompose the 18 seats.
You can grab a PDF template of different screenshot possibilities you might like by downloading here.
Here are some possibilities:
Distributive Property & Simplifying Expressions
As I’ve mentioned in my Progression of Multiplication post, the distributive property appears for the first time in the grade 4 math curriculum and appears repeatedly even into grade 9 when we use distribution with variables.
This task can provide a great opportunity for educators to hit on this very important concept again by encouraging the use of distribution or “splitting the array” into more manageable chunks. Here’s a sample of how you might consider applying distribution and simplifying whole number expressions with your class.
Please note that I’ve taken a simple example for junior grades and extended to examples that are more complex for intermediate grades that include the use of brackets and can introduce conversations about order of operations.
Workshop Exemplars
Recently, I worked with the teaching staff at Roseland Public School and we did the Airplane Problem.
After the predictions for number of seats, I challenged the groups to:
Create any numerical expression that could represent the seat configuration (or array of seats) for the airplane and use your manipulatives to represent your expression concretely.
Then, in number talk fashion, we had each person share what numerical expression(s) they saw. Here’s a few screenshots of what came out:
Simplifying Algebraic Expressions and Solving Algebraic Equations
We can extend this task even further to begin working in the Patterning and Algebra strand and even hit our Number Sense and Algebra strands in grade 9 applied and academic.
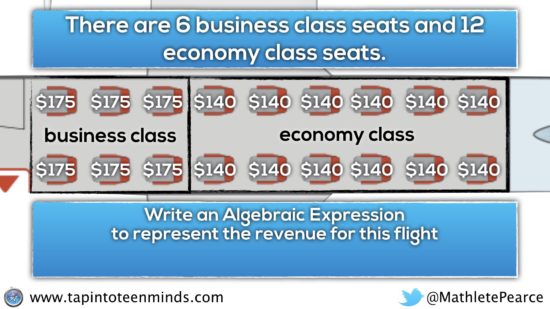
By simply creating a business class and economy class section on the airplane, we can have students predict how much revenue a sold out flight might generate:
By having students make predictions, the question is open and allow students to make predictions based on numbers that are friendly to them.
After sharing out, I might have students write a number sentence to represent the revenue for the flight.
I would encourage students trying to finding more ways to represent the same expression. I encourage students to look for ways to decompose their number sentence to allow for the use of mental math without a calculator.
Here is one such example:
Then, I might have students create expressions and/or equations to represent the Revenue for that flight. I might begin with a more open question where they set prices of seats, but then after sharing out, we might look at more specific questions like these:
Eventually, I might suggest to students that I want to keep the pricing for business and economy class at the prices indicated and ask:
What equation could represent revenue for this particular flight?
Then, we can work with substituting values into equations and solving for unknowns, which is a useful skill for all intermediate math classes.
I’ve put together a few consolidation silent solution videos, if you’re interested in helping you generate some ideas.
Exploring Quadratic Relations
My last suggestion for a grade 10 applied or academic teacher would be to engage in some of the linear equation work sampled above and then head towards quadratics.
Here’s an example that could work nicely:
On a flight where all 18 seats have equal value on this particular plane and trip, research conducted by Air Canada has shown that a price of $200 per seat produces a very high probability of selling 10 seats. For every $10 increase in price, they sell 1 less seat. How much revenue can Air Canada expect on a flight where the seats are priced at $160 each?
Some follow-up work might include having students complete a table of revenue vs. seats sold to expose the second differences of this quadratic relation. Work can then be done to connect the table, to the graph of the parabola, to quadratic form of an equation and factored form of an equation.
I hope to find some time in the near future to create some visuals for this portion of the activity. If this is something you’re hoping for, please comment below so I can get motivated to get the work done!
Purposeful Practice
One of the most common questions I receive when delivering workshops or via email is not around the actual use of a 3 act math task, but more about what to do after the task is complete. This is definitely a fuzzy area as I think this would most likely look different from classroom to classroom based on your own student learning needs. This is also tricky with this post in particular since I’ve tried to hit every grade level from grade 1 to grade 10. What I’ve tried to do was to give you an idea of what I might have my grade 9 applied and/or academic students work on after completing this task with the solving equations extensions. It might look something like this.
Disclaimer
**I’m going to come clean here and tell you that my video and the plane we are exploring actually don’t match! A teacher noticed this because the plane we are finding seats for is an Air Canada flight and Porter is the only airline that actually flies from Windsor to Billy Bishop Airport. If any of your students pick up on this, they’re pretty slick!**
New to Using 3 Act Math Tasks?
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Access Other Real World Math Tasks
Search More 3 Act Math Tasks
Grade 2 [2.B1.1, 2.B1.3, 2.B2.1, 2.B2.2, 2.B2.3, 2.B2.4, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3]
Grade 3 [3.B1.5, 3.B2.1, 3.B2.3, 3.B2.7, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3]
Grade 4 [4.B2.1, 4.B2.4, 4.E2.5, 4.E2.6, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 5 [5.B1.7, 5.B2.9, 5.D1.3, 5.D1.6, 5.E2.6, 5.F1.2, 5.F1.5, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 6 [6.B2.12, 6.B2.9, Data Management and Probability - DP3, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 7 [7.B1.3, 7.B1.4, 7.B1.7, 7.B2.2, 7.B2.3, 7.C1.1, 7.C1.2, 7.C1.3, 7.C1.4, 7.D1.6, Data Management and Probability - DP3, Geometry and Spatial Sense - GS1, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 8 [8.B1.4, 8.B2.5, 8.C1.1, 8.C1.2, 8.C1.3, 8.C1.4, Data Management and Probability - DP1, Data Management and Probability - DP3, Geometry and Spatial Sense - GS2, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 9 [9.B3.5, 9.C3.1, 9.C3.2, 9.C3.3]
Kindergarten [k.15.1, k.15.10, k.15.2]
MAP4C [Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MAT1LMAT2LMBF3C [Data Management - DM1, Data Management - DM2, Geometry and Trigonometry - GT1, Geometry and Trigonometry - GT2, Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MCF3M [Exponential Functions - EF2, Quadratic Functions - QF1, Quadratic Functions - QF2, Quadratic Functions - QF3, Trigonometric Functions - TF1, Trigonometric Functions - TF3]
MCR3U [Characteristics of Functions - CF1, Characteristics of Functions - CF2, Exponential Functions - EF2, Exponential Functions - EF3, Trigonometric Functions - TF3]
MCT4C [Exponential Functions - EF1, Trigonometric Functions - TF3]
MCV4U [Derivatives and Their Applications - DA2]
MDM4U [Counting and Probability - CP2, Organization of Data For Analysis - DA2, Probability Distributions - PD1, Statistical Analysis - SA1, Statistical Analysis - SA2]
MEL4EMFM1P [Linear Relations - LR1, Linear Relations - LR2, Linear Relations - LR3, Linear Relations - LR4, Measurement and Geometry - MG1, Measurement and Geometry - MG2, Measurement and Geometry - MG3, Number Sense and Algebra - NA1, Number Sense and Algebra - NA2]
MFM2P [Measurement and Trigonometry - MT1, Measurement and Trigonometry - MT2, Measurement and Trigonometry - MT3, Modelling Linear Relations - LR1, Modelling Linear Relations - LR2, Modelling Linear Relations - LR3, Quadratic Relations in y = ax^2 + bx + c Form - QR1, Quadratic Relations in y = ax^2 + bx + c Form - QR2, Quadratic Relations in y = ax^2 + bx + c Form - QR3]
MHF4U [Characteristics of Functions - CF3, Exponential and Logarithmic Functions - EL2, Exponential and Logarithmic Functions - EL3]
MPM1D [AG3, Analytic Geometry - AG1, Analytic Geometry - AG2, LR1, LR2, LR3, MG1, MG2, MG3, NA1, Number Sense and Algebra - NA2]
MPM2D [AG1, AG2, AG3, QR2, Quadratic Relations - QR3, Quadratic Relations - QR4, T2, T3]
Functions [F-BF.1, F-BF.3, F-IF.4, F-LE.1, F-LE.2, F-LE.3, F-TF.5]
Geometry [G-C.5, G-C.8, G-C.9, G-GMD.3, G-GMD.4, G-GPE.4, G-GPE.5, G-GPE.7, G-MG.1, G-MG.2, G-SRT.11]
Grade 1 [1.NBT.4, 1.OA.1, 1.OA.6, 1.OA.A.1, 1.OA.B.3, 1.OA.B.4, 1.OA.C.5, 1.OA.C.6]
Grade 2 [2.NBT.5, 2.NBT.B.5, 2.NBT.B.8, 2.NBT.B.9, 2.OA.2, 2.OA.A.1, 2.OA.B.2]
Grade 3 [3.MD.C.5, 3.NBT.2, 3.NF.1, 3.NF.2, 3.NF.3, 3.NF.A.1, 3.OA.1, 3.OA.5, 3.OA.9]
Grade 4 [4-MD.3, 4.MD.1, 4.MD.2, 4.NBT.6, 4.NF.3, 4.NF.5, 4.NF.6, 4.OA.1, 4.OA.5]
Grade 5 [5.B1.7, 5.D1.3, 5.D1.6, 5.MD.1, 5.MD.3, 5.MD.4, 5.MD.5, 5.NBT.2, 5.NBT.3, 5.NBT.6, 5.NBT.7, 5.NF.1, 5.NF.2, 5.NF.3, 5.NF.4, 5.NF.5, 5.OA.1, 5.OA.2, 5.OA.3]
Grade 6 [6.EE.1, 6.EE.2, 6.EE.5, 6.EE.6, 6.EE.7, 6.G.1, 6.G.2, 6.NS.1, 6.NS.3, 6.NS.6, 6.NS.B.3, 6.NS.C.6, 6.NS.C.7, 6.NS.C.8, 6.RP.1, 6.RP.2, 6.RP.3, 6.RP.A.1, 6.RP.A.2, 6.RP.A.3, 6.RP.A.3.C]
Grade 7 [7.EE.3, 7.EE.4, 7.EE.A.1, 7.G.3, 7.G.4, 7.G.6, 7.NS.A.1, 7.NS.A.2, 7.RP.1, 7.RP.3, 7.RP.A.2.B, 7.RP.A.3, 7.SP.2, 7.SP.5, 7.SP.6]
Grade 8 [8.EE.1, 8.EE.5, 8.EE.6, 8.EE.7, 8.EE.8, 8.F.2, 8.F.3, 8.F.4, 8.F.5, 8.G.5, 8.G.6, 8.G.7, 8.G.9, 8.SP.1]
Grade 9Kindergarten [K.CC.A.1, K.NBT.A.1, K.OA.A.1, K.OA.A.2, K.OA.A.3]
Practice [MP.1, MP.2, MP.3, MP.4, MP.6, MP.7]
Statistics & Probability [S-ID.6, S-MD.4]



















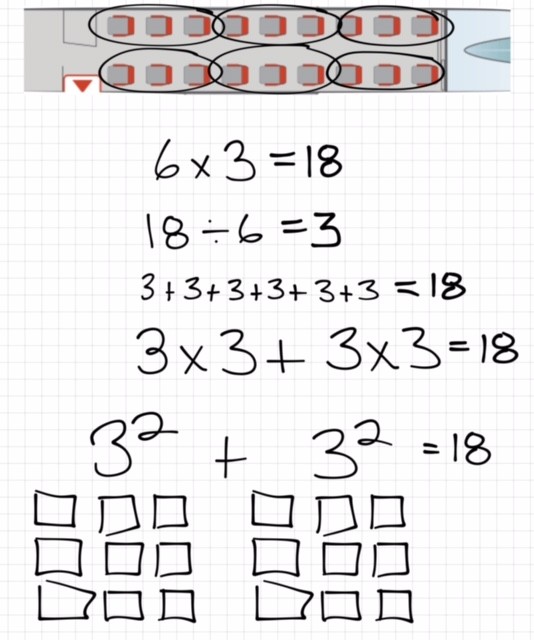
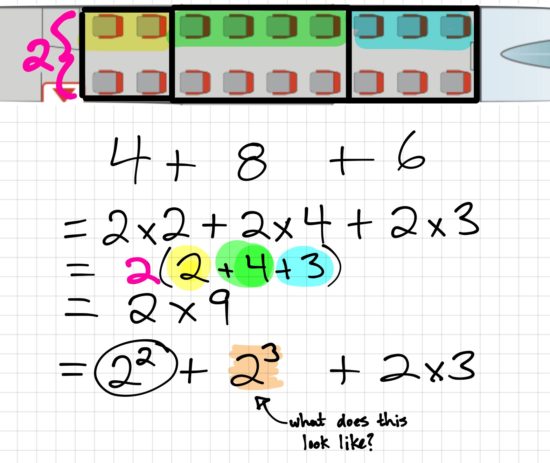




Really neat, which is an understatement I realize.
Would love visuals for Exploring Quadratic Relations part – thanks for all you creative ideas and passion for maths