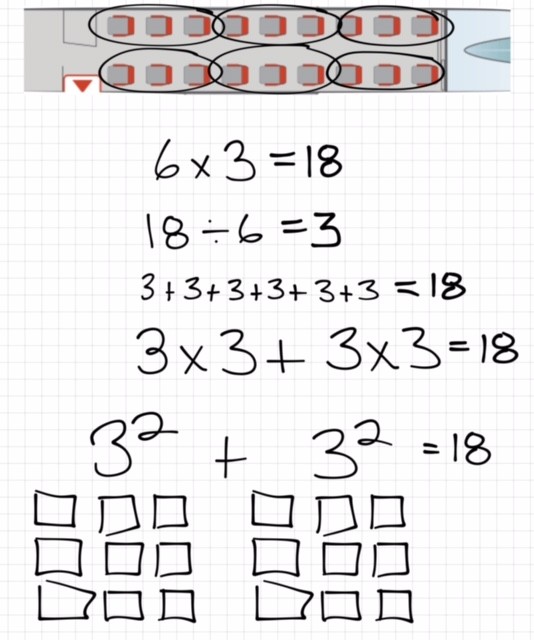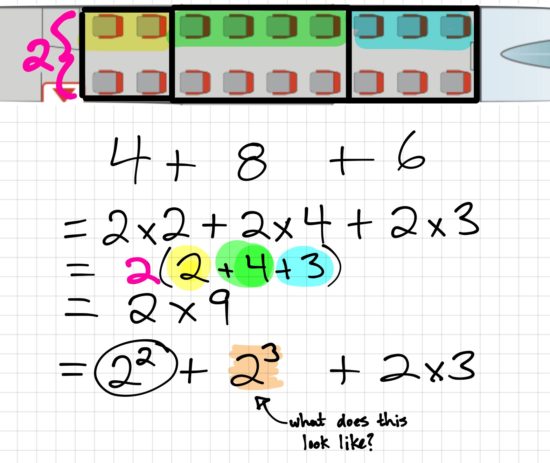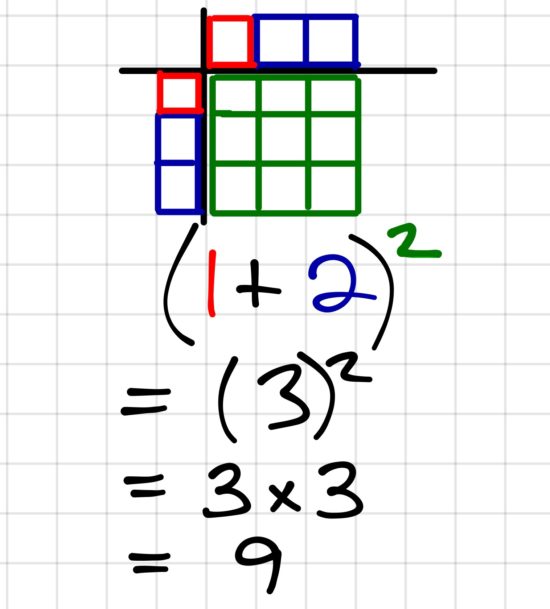GECDSB School Based Learning Sessions (SBL)
Thursday March 2nd, 2017
Thanks for inviting me to learn with you on your school based learning day! The group was energetic and excited to learn about meaningful manipulative use, spatial reasoning, some counting principles, visualizing numerical expressions, some multiplication/division and the importance of concreteness fading!
Here’s a summary of what we explored today throughout all three 100-minute blocks:
The GECDSB Mathematics Strategy
Mathematical Proficiencies
The full GECDSB Mathematics Vision is here.
Paying Attention to Spatial Reasoning
Warm-Up: How Do You See the Dots?
We did a quick Dot-Card warm-up asking you to visualize how you saw a series of dots on the screen. We went around the table and it seemed that everyone had a different perspective.
Here’s some of the ways you might have visualized the dots:
Counting Principles
We briefly discussed the importance of counting and quantity principles like subitizing and unitizing. A full summary is below:
[postshortcode the_query=”p=18603″]
A Spatial Reasoning Task
Both the primary and junior groups were interested in some tasks that might help students with their spatial reasoning skills.
One that came to mind immediately was from NRich.org:
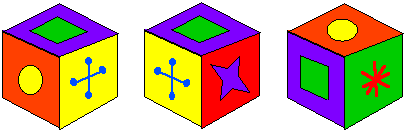
A Puzzling Cube
Here are the six faces of a cube – in no particular order:
Here are three views of the cube:
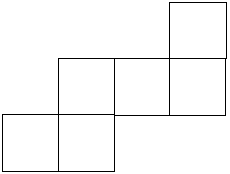
Can you deduce where the faces are in relation to each other and record them on the net of this cube?
You can use this interactivity to try out your ideas. You will still have to visualize the cube folded up!
Check out the interactive version here.
Then we took some time to explore a 3 act math task with a very low-floor and high-ceiling, called the Airplane Problem:
[threeactshortcode the_query=”post_type=realworldmath&p=18652″]
In the airplane problem, we made predictions, explored subitizing and unitizing.
After the predictions for number of seats, I challenged the group to:
Create any numerical expression that could represent the seat configuration (or array of seats) for the airplane and use your manipulatives to represent your expression concretely.
Then, in number talk fashion, we had each person share what numerical expression(s) they saw. Here’s a few screenshots of what came out:
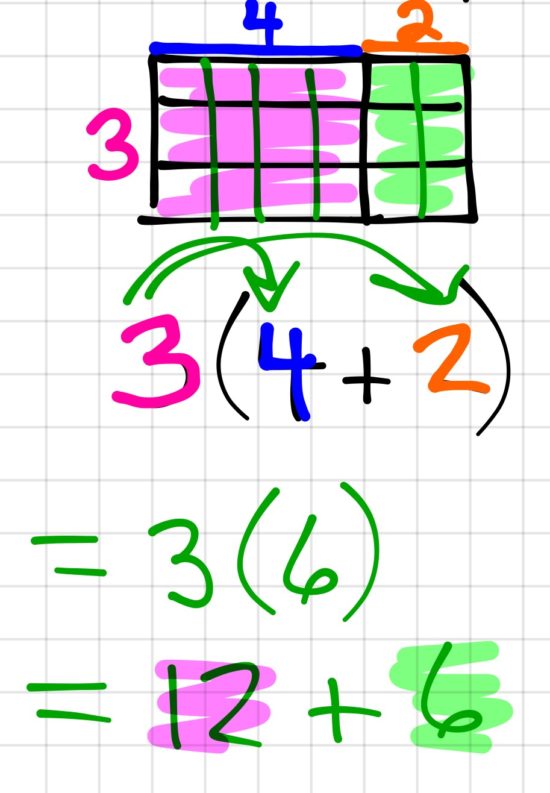
Visualizing the Order of Operations
With our intermediate friends, we explored the Airplane Problem and also looked at different ways to write the seat configuration using as many different numerical expressions as possible. Some great conversations were had and it led us to think about some of our order of operations work in the intermediate grades.
Here’s some of where it led:
We also took some time to visualize the order of operations in various ways including these:
See the whole playlist of visualizing order of operations videos here.
Extending to Multiplication and Division
Finally, with the junior group, we explored the Donut Delight 3 act math task where we played with multiplication to predict how many donuts there were in the “double hundred dozen” box and then used repeated subtraction to lead to a flexible division algorithm for division when we tried to find how many layers there were.
[threeactshortcode the_query=”post_type=realworldmath&p=18719″]
While we didn’t explore the progression of multiplication explicitly, the following post might be useful to extend some of the thinking from the donut delight task.
[postshortcode the_query=”p=17501″]
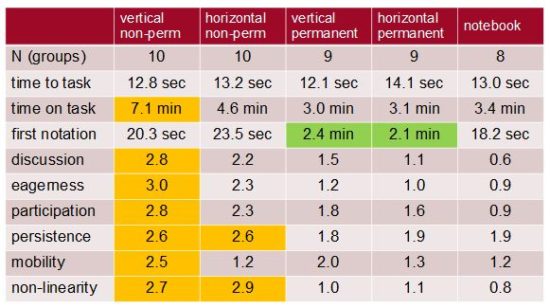
Vertical Non-Permanent Surfaces
During the second 100-minute block, some discussion arose from the use of whiteboards – also known as “vertical non-permanent surfaces (VNPS)”. Peter Liljedahl from Simon Fraser University has done extensive research on Vertical Non-Permanent Surfaces (VNPS) including his paper Building Thinking Classrooms. In his research, he has found that standing and writing on non-permanent surfaces like chalkboards or whiteboards is very effective for engagement, time-to-task and time-on-task in mathematics class:
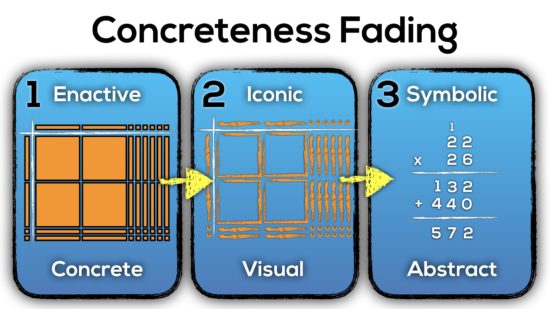
Concreteness Fading
We attempted to summarize the use of manipulatives on a continuum called “Concreteness Fading”. While the name suggests that concrete manipulatives fade away over time, it is important to remember that they fade away with one layer of abstraction and then reappear as a new layer is “piled” on.
Hope you folks found this professional learning experience useful.
I’d be delighted to come back and learn alongside you all again sometime soon!