SNACK TIME
WHOLE NUMBER PARTITIVE DIVISION RESULTING IN A FRACTIONAL
Dividing whole numbers through partitive division resulting in a fractional quotient.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will determine how to partition the cheese in order to fair share it based on the number of crackers.
Intentionality…
In this task, students will represent the partitioning of cheese slices in order to fair share them amongst the crackers without leaving any cheese leftover. At this point, students may not have a lot of experience dividing when the dividend is less than the divisor. This new experience will likely emerge practical tools for partitioning such as concrete materials, a bar model and/or a linear model.
Through the consolidation, students are prompted to make conjectures about the behaviour of this structure of division. For example, “I already know the whole amount of cheese (the dividend) and the quantity of crackers (the divisor). What I am trying to reveal is a rate, or how much per one cracker (part).”
You might also explore equivalent representations of the quotient. This could reveal that the quotient is the dividend (numerator) over the divisor (denominator).
Some of the big ideas that may emerge through this task include:
- Partitive division is one of the two structures of division;
- In partitive division, the dividend is the quota and the divisor is the number of parts or groups;
- When dividing partitively, the quotient reveals a rate, how many per part (or the quota per group);
- The quotient can be expressed as any fraction equivalent to the dividend over the divisor;
- The number of partitions determines the fraction unit and gives the quantity its name (i.e.: partitioning a whole into 5 parts creates “5 fifth” parts);
- Different denominators can be used to represent equivalent quantities.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this 30 second video.
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up include:
- I see a block of cheese.
- I wonder if it is cheddar.
- I see crackers.
- I wonder how many crackers there are.
- I saw three slices being cut.
- I wonder if he is going to cut anymore.
At this point, you can answer any wonders that you can cross off the list right away.
Estimation: Prompt
After students share out with the class, tell a story about the situation from the video and how annoying it is when you just randomly break off pieces of cheese for your crackers and then end up with too many crackers left with not enough cheese.
So, the question we begin with is:
How could the cheese be cut to split evenly with the crackers?
Make an estimate.
Encourage students to begin crafting an estimate. If some students quickly arrive at an estimate, encourage students to explain their thinking.
How many crackers did they estimate and why does their final estimate make sense?
Emphasize that you will be looking to see their thinking represented either concretely or pictorially (this representation might be in addition to their abstract representation if students decide to divide using an algorithm). You might consider allowing each student time to think through their plan for 3-5 minutes before asking them to collaborate with a partner or a small-group. This dedicated time for personal reflection allows all students to enter the conversation with the advantage of time to think through their current understanding before being potentially overwhelmed or bulldozed by the ideas of others.
Keep in mind, the intent here is to encourage all students to enter into this task. Since all students are estimating the number of crackers, this opens the door for a student who may not feel as confident to make an estimate that is easier for partitively dividing (or fair sharing) the 3 slices of cheese across the number of crackers. Estimating a number of crackers that is a multiple of 3 will make this process easier for students, so keep an eye for students who select 9, 12, or 15 as their number of crackers.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Some students might quickly comment that it is difficult to know for sure without confirming the number of crackers. When this point is expressed by a student, share the following video.
Now that students are aware of exactly how many crackers there are (12) and how many slices of cheese (3), we can refine our prompt for students:
How much of one slice of cheese can we put on each cracker?
Refining this question to become more specific will encourage students to relate the quantity of cheese relative to a whole slice per cracker in order to more specifically encourage the use of fractional language or notation when describing the quotient.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete manipulatives such a fraction strips or relational rods
- Paper folding
- A pictorial representation such as a bar model
- A number line
Have students share their strategies and reasoning for how they would partition the cheese . Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Concrete With Square Tiles
I wanted to use the square tiles to show the slices of cheese. I did not know how many tiles to use for each slice, but I knew that one would only be enough for three crackers. I also knew two wasn’t enough either, that would be 6 crackers. So then I went to three tiles, and I counted them. I could only share cheese with nine crackers. I tried four tiles, and that works. So I know that if I cut each slice into four pieces, then I have enough for all 12 crackers. If every cracker gets one of the four parts of a slice, then they get one-fourth of a slice.
Student Approach #2: Paper Folding
I cut three strips of paper, one for each slice of cheese. I started by folding them in half. I had six parts, enough cheese for six crackers. I folded the paper again because twelve is twice as many as six. I had each slice cut into four parts, each part was enough for one cracker. So every cracker was going to get one-fourth of a slice, or one-twelfth of all of the cheese.
Facilitator Note:
Notice that this student referenced a fraction of an individual slice as well as a fraction of the entire quantity of cheese (3 slices). Watch for other students who may be coming up with “one-fourth” or “one-twelfth” (unitless answers) and are unsure why their answers are not equivalent.
Student Approach #3: Reasoning With An Array
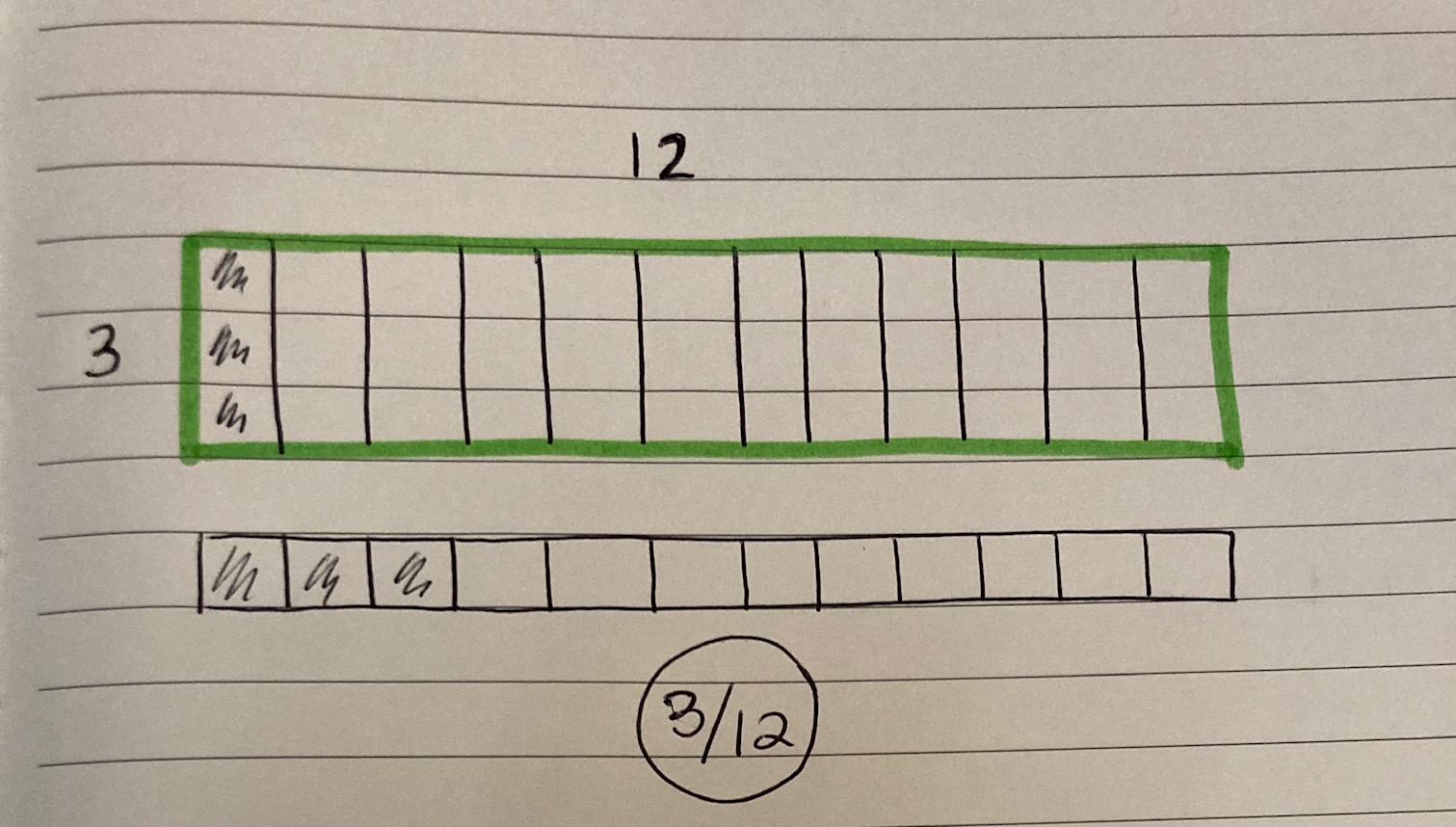
There are three slices of cheese, so I drew those first. I know that the three slices need to be split by 12 crackers. I could see that each cracker could get three parts of a slice. If a whole slice is 12 parts, and each cracker can have three, then each cracker will get three-twelfths of a slice.
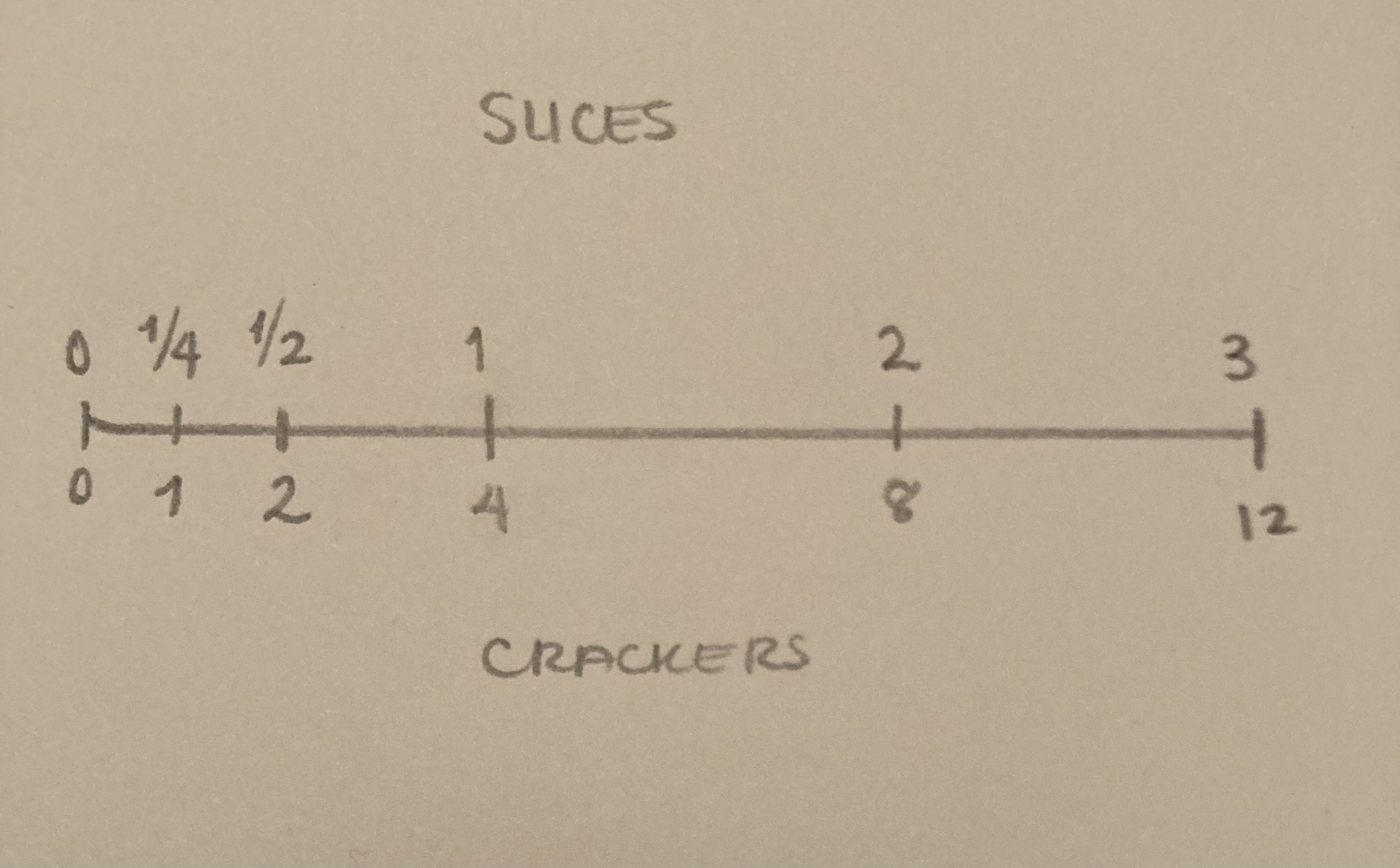
Student Approach #4: Number Line
I know that the whole is twelve crackers and three slices. So I put them at the end of my number line. I know that I am going to use all of the cheese for all of the crackers. I realized that to get to twelve, I used three slices. And that means that every slice needs to be shared by four crackers. So I split my slice in half, that’s enough for 2 crackers. And then in half again, that’s how much I will need to use for one cracker. One-fourth.
Next Moves
Reveal
Share this video to confirm student thinking.
Consolidation
Consider asking students:
What operation was used to solve this problem?
Oftentimes, students are able to solve this problem because they understand the context and what the problem is asking them to do without necessarily noticing or naming the operation. Do not be surprised if students struggle to name this operation as division, but use this as an opportunity to help them connect what they did to solve this problem to the operation.
Be sure to give students enough time to think independently and with their neighbours to debate what operation they may have used before allowing them to begin sharing out with the whole class.
The consolidation of this lesson will begin as students begin sharing out their thinking in regards to which operation was used to solve this problem.
At this point, we want to highlight that this problem was solved through division – whether the students realized it or not.
On the board, write:
3 ÷ 12
Use the consolidation of student models to analyze the behaviours of this type of division, called partitive division.
Facilitator note:
It is important for the facilitator to know and understand that there are two types of division and the following portion of the consolidation is going to help us expose one of those two types called partitive division.
Ask students:
What we were given in this task in order to help us solve the problem?
Students will share some or all of the following:
- We knew the total amount of cheese slices (3).
- We knew the total quantity of crackers (12).
- We knew that we were going to use all of the cheese, and all of the crackers.
- We knew that we did not have enough slices for all of the crackers, so we had to cut (partition) the slices.
What do we want to know?
- We want to know how to cut (partition) the cheese to give an equivalent amount of cheese to use per cracker.
Examine the quotient: one-fourth of one slice. Encourage students to consider (through questioning or by highlighting a student’s solution) whether there is any other possible way to partition the slices other than fourths. Through this question, our goal is to reveal equivalence and possibly see the relationship between three-twelfths and the original quantities and division sentence.
As you plan and prepare your consolidation, you might consider reviewing this silent solution animation that unpacks some possible representations you might see emerging from student work including partitioning and fair sharing (similar to student approach #1), using an array (similar to student approach #3), a linear bar model, and a double number line (similar to student approach #4):
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
How many cheese slices per cracker will result if you share the two slices equally with no cheese leftover?
Use a model of your choice to justify your answer.
For Consolidation Prompt #1, there are two reveal videos you could consider sharing with students that demonstrate two different approaches.
The first video demonstrates an approach where each slice of cheese is partitioned into thirds because there are 3 crackers to share the cheese to.
The second video demonstrates an approach that suggests the student understands that cutting each slice into thirds will ensure that there will be enough equivalent fractional parts to share to each of the three crackers. However, instead of cutting into thirds, this approach suggests that the student realizes that there will be more than one equivalent part given to each cracker. Rather than cutting the cheese into more smaller parts than necessary, the cheese is cut into two-third parts to keep larger chunks of cheese together.
Both approaches result in the same rate of 2 third slices of cheese per cracker.
Consolidation Prompt #2:
How many cheese slices per cracker will result if you fair share the two slices to 5 crackers?
Use a model of your choice to justify your answer.
The following silent solution animation shows a real world linear approach that could easily be connected to a double number line:
The result is a rate of 2 fifth slices of cheese per cracker.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!