Ontario Alignment By Overall Expectation
Grade 4 [Measurement - M1, Number Sense and Numeration - NS1]
Grade 5 [Measurement - M1, Number Sense and Numeration - NS1]
Grade 6 [Measurement - M1, Number Sense and Numeration - NS3]
Grade 7 [Measurement - M1, Number Sense and Numeration - NS3]
Grade 8 [Measurement - M1, Number Sense and Numeration - NS3]
MAT1L
MAT2L
MFM1P [Measurement and Geometry - MG1, Number Sense and Algebra - NA1]
Sparking Curiosity to Promote Conceptual Understanding of Measurement and Unit Conversions

This 3 act math task was inspired by a question on the 2018 EQAO Grade 6 Assessment of Mathematics Ontario standardized test that rockstar teacher Shelley Iler brought to the attention of Yvette Lehman and I recently. Interestingly enough, only 34% of students in Ontario answered this multiple choice question correct and when we dive into the question, you’d understand why! Not only does it have multiple steps, but it also ties in so many different elements of proportional reasoning that many students struggle with in isolation, let alone when mixed together in a task like this one.
Although this task was inspired from a question on a Grade 6 standardized math test, the visual prompts I’ve created make the task accessible by students in all grades including Kindergarten. Just be sure to modify how far you go with it depending on your group.
Here’s the question:
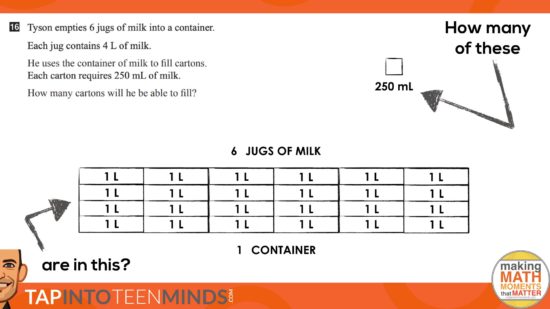
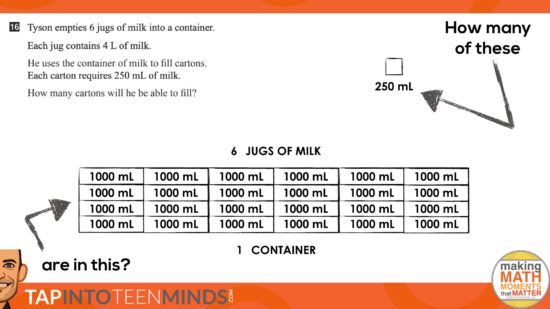
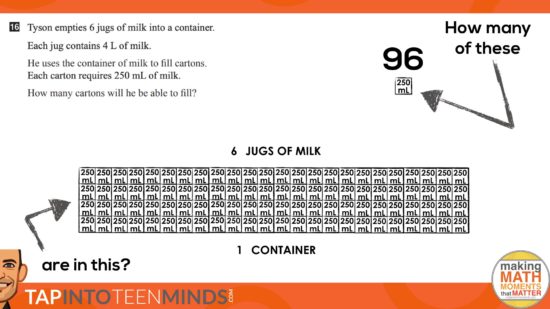
Tyson empties 6 jugs of milk into a container.
Each jug contains 4 L of milk.
He uses the container of milk to fill cartons.
Each carton requires 250 mL of milk.
How many cartons will he be able to fill?
You can find it in the 2018 Release Materials of the EQAO Grade 6 Assessment of Mathematics.
You’ll also notice that many of the visuals I will share for the inquiry portion of this task makeover are from my website MathIsVisual.com, but later in this post we have a summary of how one might consolidate the learning to make connections.
So let’s get going!
Act 1: Sparking Curiosity
Show students this video.
There are instructions to pause the video to engage in a notice and wonder.
Alternatively, you could show this animated gif:

While I typically have students do a rapid write to jot down what they notice and what they wonder, if we are in a kindergarten through grade 3(ish) class, it’s likely that students are sitting with you on the carpet. In that case, it might make more sense for them to think of what they notice and wonder in their minds and then share out with their partners through a think, pair, share.
Remember that articulating students can notice and wonder ANYTHING and EVERYTHING that comes to mind.
Here’s some of the “everything and anything” students noticed and wondered on chart paper (remembering that nothing with numbers would not be shared yet):
- I a square and a rectangle.
- I notice the square is all white, then only a part of the rectangle is white.
- I notice that it looks like liquid is draining from the square into the rectangle.
- I wonder how many squares worth of white it would take to fill the rectangle?
- I wonder what the white actually “is”?
- And many others…
The wonder we landed on was:
How many squares will it take to fill (or cover) the rectangle?
As usual, we then had students make an estimate using their spatial reasoning skills.
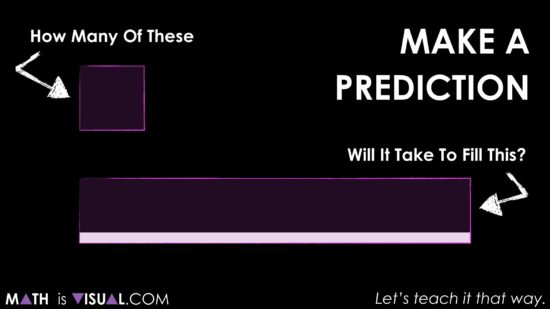
In one Grade 5/6 classroom I used this task in, I wish I had set up my tripod to capture the mathematical discourse. In particular, the estimates students were making were so great.
For example, one student said:
I think 5, because 1 whole square was white and it dumped into the rectangle to fill only 1 fifth of the rectangle. So that means it will take 5 squares to fill the rectangle.
Other students made estimates of 6 and 7 using similar reasoning.
After students made their estimates and shared their reasoning with the group, we revealed the result:
Alternatively, you could show this animated gif:
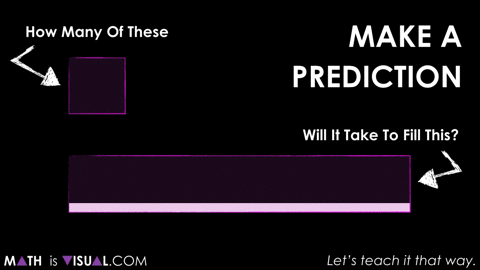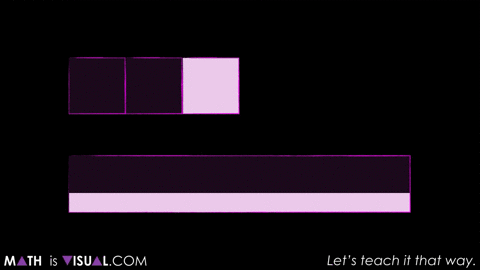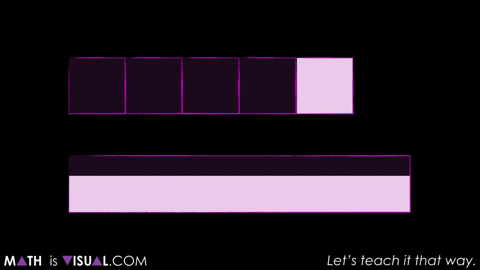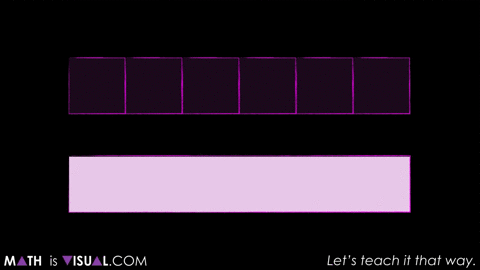
So while you might be wondering why I’d show the 3rd act during the 1st act of the task, the reality is we were just getting warmed up.
The real question is:

How many ‘little squares’ can the rectangle fill?
As you’d expect, we ask students to make estimates and share their reasoning.
This is where I REALLY wanted to have my tripod set up to record the mathematical conversations. Students were making some pretty awesome estimates and articulating their reasoning a ton.
One student said:
I think you can fill 150 little squares because 1 big square would fit 5 rows and 5 columns of little squares for a total of 25 little squares. Since we needed 6 big squares to fill the rectangle, then we can fill 6 big squares of 25 little squares for a total of 150 little squares.
Another student used similar reasoning, but thought 4 columns and 4 rows of little squares could fit in the bigger square and thus the estimate was 96 little squares.
Another student looked at the rectangle and said:
I think that the rectangle can fit 4 rows of 20 little squares, so my estimate is 80 little squares total.
The conversation was rich. What a blast!
DON’T LET STREAMING VIDEOS DERAIL YOUR LESSON!
Want to make sure this task goes off without a hitch?
Maximize your chances of Making a Math Moment That Matters for your students by downloading the video files to avoid a poor internet connection crashing your lesson!

Act 2: Reveal More Information
At this point, students were ready to be given some measured quantities to work with.
We set the stage for the context… originally there were 6 jugs of milk that were poured into a container and then poured once again into cartons. How many cartons could you fill?

The jugs had 4 litres of milk each and each carton could hold 250 mL.
With manipulatives within reach, we asked students to try to improve their estimates and use tools and representations to convince us. We weren’t going to just accept numbers or even mathematical expressions. We wanted proof!
Here’s some of what we saw:


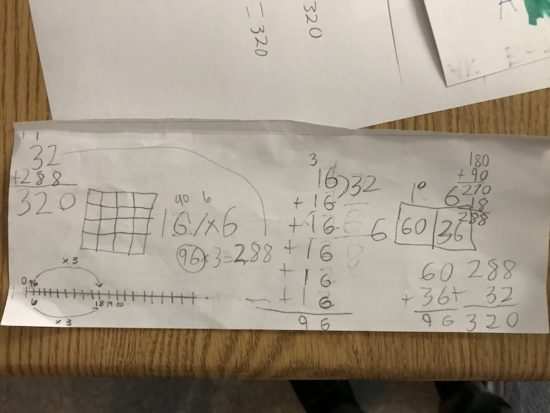

DON’T LET STREAMING VIDEOS DERAIL YOUR LESSON!
Want to make sure this task goes off without a hitch?
Maximize your chances of Making a Math Moment That Matters for your students by downloading the video files to avoid a poor internet connection crashing your lesson!

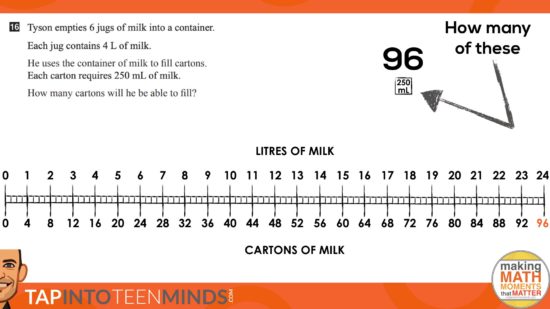
Act 3: The Big Reveal
In this particular case, we consolidated the lesson by using student work and then extended to making a connection to the double number line as a tool for thinking as well as a tool to represent their thinking.
Here’s what we were up to:
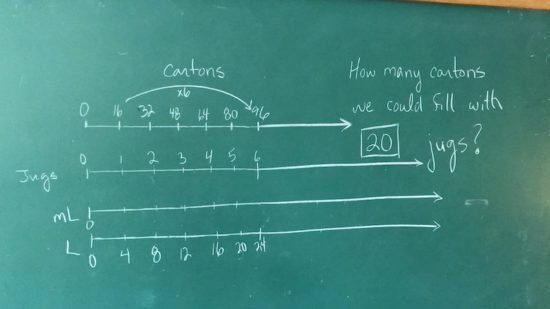
Here’s the big reveal using visuals only:
For an animated “silent solution” consolidation, check out this video here:
Here’s a handful of screen grabs of the animations:


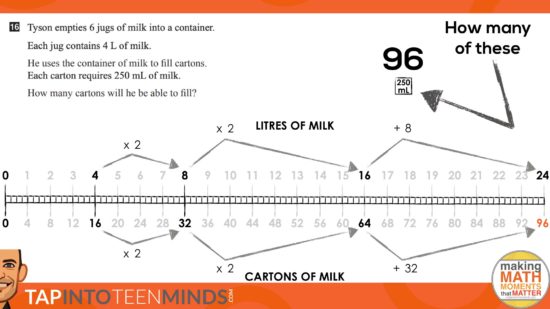

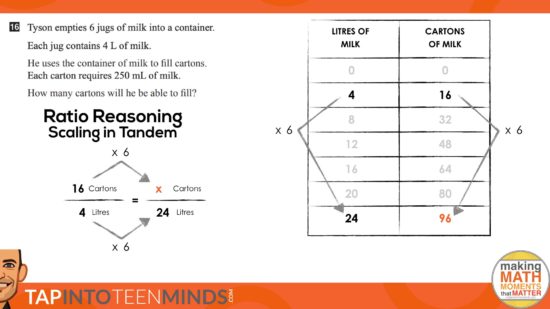

Extension Questions:
There are quite a few different directions you could go in after this.
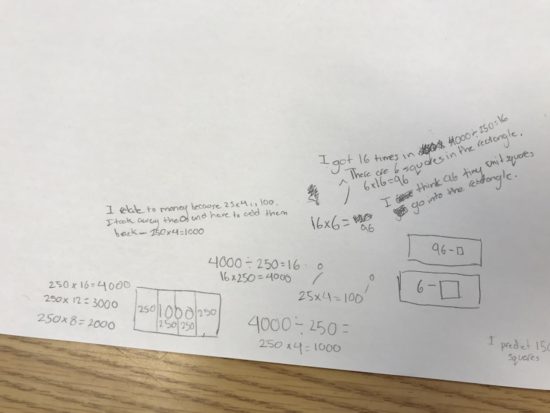
A question we challenged the students to try was to determine how many cartons you could fill with 20 jugs (big squares) of milk.
Here’s some student work:

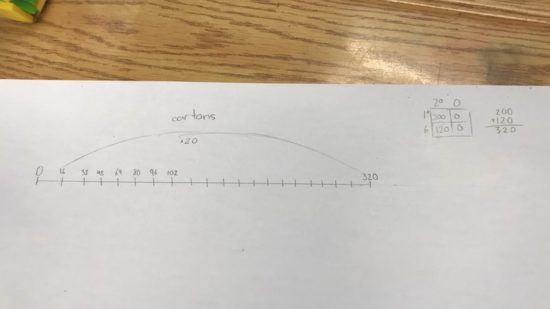

Here’s an image from the consolidation as well:

What are some other good extension questions you can think of?
Post in the comments below!
New to Using 3 Act Math Tasks?
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Access Other Real World Math Tasks
Search More 3 Act Math Tasks
Grade 2 [2.B1.1, 2.B1.3, 2.B2.1, 2.B2.2, 2.B2.3, 2.B2.4, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3]
Grade 3 [3.B1.5, 3.B2.1, 3.B2.3, 3.B2.7, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3]
Grade 4 [4.B2.1, 4.B2.4, 4.E2.5, 4.E2.6, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 5 [5.B1.7, 5.B2.9, 5.D1.3, 5.D1.6, 5.E2.6, 5.F1.2, 5.F1.5, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 6 [6.B2.12, 6.B2.9, Data Management and Probability - DP3, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 7 [7.B1.3, 7.B1.4, 7.B1.7, 7.B2.2, 7.B2.3, 7.C1.1, 7.C1.2, 7.C1.3, 7.C1.4, 7.D1.6, Data Management and Probability - DP3, Geometry and Spatial Sense - GS1, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 8 [8.B1.4, 8.B2.5, 8.C1.1, 8.C1.2, 8.C1.3, 8.C1.4, Data Management and Probability - DP1, Data Management and Probability - DP3, Geometry and Spatial Sense - GS2, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 9 [9.B3.5, 9.C3.1, 9.C3.2, 9.C3.3]
Kindergarten [k.15.1, k.15.10, k.15.2]
MAP4C [Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MAT1LMAT2LMBF3C [Data Management - DM1, Data Management - DM2, Geometry and Trigonometry - GT1, Geometry and Trigonometry - GT2, Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MCF3M [Exponential Functions - EF2, Quadratic Functions - QF1, Quadratic Functions - QF2, Quadratic Functions - QF3, Trigonometric Functions - TF1, Trigonometric Functions - TF3]
MCR3U [Characteristics of Functions - CF1, Characteristics of Functions - CF2, Exponential Functions - EF2, Exponential Functions - EF3, Trigonometric Functions - TF3]
MCT4C [Exponential Functions - EF1, Trigonometric Functions - TF3]
MCV4U [Derivatives and Their Applications - DA2]
MDM4U [Counting and Probability - CP2, Organization of Data For Analysis - DA2, Probability Distributions - PD1, Statistical Analysis - SA1, Statistical Analysis - SA2]
MEL4EMFM1P [Linear Relations - LR1, Linear Relations - LR2, Linear Relations - LR3, Linear Relations - LR4, Measurement and Geometry - MG1, Measurement and Geometry - MG2, Measurement and Geometry - MG3, Number Sense and Algebra - NA1, Number Sense and Algebra - NA2]
MFM2P [Measurement and Trigonometry - MT1, Measurement and Trigonometry - MT2, Measurement and Trigonometry - MT3, Modelling Linear Relations - LR1, Modelling Linear Relations - LR2, Modelling Linear Relations - LR3, Quadratic Relations in y = ax^2 + bx + c Form - QR1, Quadratic Relations in y = ax^2 + bx + c Form - QR2, Quadratic Relations in y = ax^2 + bx + c Form - QR3]
MHF4U [Characteristics of Functions - CF3, Exponential and Logarithmic Functions - EL2, Exponential and Logarithmic Functions - EL3]
MPM1D [AG3, Analytic Geometry - AG1, Analytic Geometry - AG2, LR1, LR2, LR3, MG1, MG2, MG3, NA1, Number Sense and Algebra - NA2]
MPM2D [AG1, AG2, AG3, QR2, Quadratic Relations - QR3, Quadratic Relations - QR4, T2, T3]
Functions [F-BF.1, F-BF.3, F-IF.4, F-LE.1, F-LE.2, F-LE.3, F-TF.5]
Geometry [G-C.5, G-C.8, G-C.9, G-GMD.3, G-GMD.4, G-GPE.4, G-GPE.5, G-GPE.7, G-MG.1, G-MG.2, G-SRT.11]
Grade 1 [1.NBT.4, 1.OA.1, 1.OA.6, 1.OA.A.1, 1.OA.B.3, 1.OA.B.4, 1.OA.C.5, 1.OA.C.6]
Grade 2 [2.NBT.5, 2.NBT.B.5, 2.NBT.B.8, 2.NBT.B.9, 2.OA.2, 2.OA.A.1, 2.OA.B.2]
Grade 3 [3.MD.C.5, 3.NBT.2, 3.NF.1, 3.NF.2, 3.NF.3, 3.NF.A.1, 3.OA.1, 3.OA.5, 3.OA.9]
Grade 4 [4-MD.3, 4.MD.1, 4.MD.2, 4.NBT.6, 4.NF.3, 4.NF.5, 4.NF.6, 4.OA.1, 4.OA.5]
Grade 5 [5.B1.7, 5.D1.3, 5.D1.6, 5.MD.1, 5.MD.3, 5.MD.4, 5.MD.5, 5.NBT.2, 5.NBT.3, 5.NBT.6, 5.NBT.7, 5.NF.1, 5.NF.2, 5.NF.3, 5.NF.4, 5.NF.5, 5.OA.1, 5.OA.2, 5.OA.3]
Grade 6 [6.EE.1, 6.EE.2, 6.EE.5, 6.EE.6, 6.EE.7, 6.G.1, 6.G.2, 6.NS.1, 6.NS.3, 6.NS.6, 6.NS.B.3, 6.NS.C.6, 6.NS.C.7, 6.NS.C.8, 6.RP.1, 6.RP.2, 6.RP.3, 6.RP.A.1, 6.RP.A.2, 6.RP.A.3, 6.RP.A.3.C]
Grade 7 [7.EE.3, 7.EE.4, 7.EE.A.1, 7.G.3, 7.G.4, 7.G.6, 7.NS.A.1, 7.NS.A.2, 7.RP.1, 7.RP.3, 7.RP.A.2.B, 7.RP.A.3, 7.SP.2, 7.SP.5, 7.SP.6]
Grade 8 [8.EE.1, 8.EE.5, 8.EE.6, 8.EE.7, 8.EE.8, 8.F.2, 8.F.3, 8.F.4, 8.F.5, 8.G.5, 8.G.6, 8.G.7, 8.G.9, 8.SP.1]
Grade 9Kindergarten [K.CC.A.1, K.NBT.A.1, K.OA.A.1, K.OA.A.2, K.OA.A.3]
Practice [MP.1, MP.2, MP.3, MP.4, MP.6, MP.7]
Statistics & Probability [S-ID.6, S-MD.4]

Trackbacks/Pingbacks