Ontario Alignment By Overall Expectation
Contextual Tasks for Practicing Solving Systems of Linear Equations
There has been a lot of requests for more contextual and/or 3 act math tasks related to solving systems of linear equations when I work with teachers. A big realization I’ve come to this past year is that making students curious with contextual tasks doesn’t necessarily have to involve a relevant question. Dan Meyer has discussed it multiple times (like here and here), but it still takes a lot of reflection to start identifying what is important when trying to hook your students in.
Continuing the series of Tech Weight and the Tech Weight Sequel, we take the same context of weighing random items to give us some additional practice. You’ll quickly notice that these tasks are definitely contrived, but I still find tasks like these useful if introduced as a challenge to my students. Even though they REALLY don’t care how much each item weighs, they DO enjoy the challenge of solving the problem. The media and 3 act format gives them an easy entry into the task. After allowing students to intuitively solve simple systems of linear equations like in the Counting Candy Sequel or the Tech Weight Sequel, you can use these tasks as a way to practice substitution and/or elimination as a way to solve algebraically.
Task 1: Sticky Situation
Act 1 – Introduce the Task
Show students this video.
Ask students what they are wondering? What questions come to mind?
After discussing with a group, help direct the focus to the question:
How much does each weigh?
Students can make predictions and argue why they believe their guess is best.
Act 2 – Reveal Some Information
Show students scene 1.
Alternatively, you can show students the following images:
The Weight of 4 bottles of glue and 5 glue sticks
The weight of 4 bottles of glue and 5 glue sticks is 679 grams.
The Weight of 3 bottles of glue and 12 glue sticks
The Weight of 3 bottles of glue and 12 glue sticks is 680 grams.
Now, students can try to solve this system intuitively, by graphing or algebraically with substitution or elimination.
Act 3 – Reveal Solution
Show students the solution video.
Alternatively, you can show students these images:
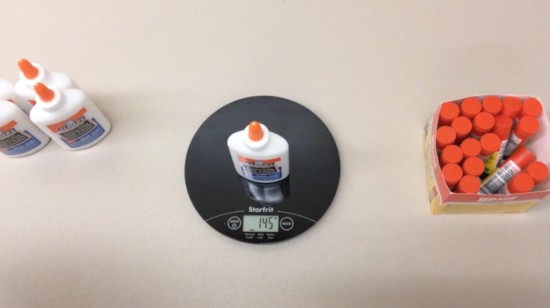
The weight of one glue bottle is 145 grams:
The weight of one glue stick is 21 grams:
At this point, your students should notice that their answers are close to these weights, but not exact.
Why might that be?
What extraneous variables could influence the results?
Task 2: Write N’ Erase
Act 1 – Introduce The Problem
Show students this video.
They will already know the question, so move on to Act 2…
Act 2 – Reveal Some Information
Show students scene 1.
Alternatively, you can show students the following images:
The weight of 13 pens and 5 packs of correction tape
The weight of 13 pens and 5 packs of correction tape is 166 grams:
The weight of 6 pens and 3 packs of correction tape
The weight of 6 pens and 3 packs of correction tape is 88 grams:
Now, students can try to solve this system intuitively, by graphing or algebraically with substitution or elimination.
Act 3 – Show The Solution
Show students the solution video.
Alternatively, you can show students these images:
The weight of one pen is 4 grams:
The weight of one package of correction tape is 20 grams:
Again, the actual weight may differ from what students found algebraically.
Task 3: Paper Weights
Act 1 – Introduce The Problem
I find that sequel tasks like these often don’t require the “hook” as we’ve already engaged the learners to come towards the math. This task is simply additional practice prior to moving on to more traditional word problems and/or abstract problems. Thus, there is no act 1 video for this extension task.
Act 2 – Reveal Some Information
Show students scene 1.
Alternatively, you can show students the following images:
The weight of 5 large notepads and 7 small notepads
The weight of 5 large notepads and 7 small notepads is 882 grams:
The weight of 3 large notepads and 5 small notepads
The weight of 3 large notepads and 5 small notepads is 563 grams:
Now, students can try to solve this system intuitively, by graphing or algebraically with substitution or elimination.
Act 3 – Show The Solution
Show students the solution video.
Alternatively, you can show students these images:
The weight of one large notepad is 116 grams:
The weight of one small notepad is 43 grams:
Again, the actual weight may differ from what students found algebraically.
Try it out and let us know how it goes in the comments!
New to Using 3 Act Math Tasks?
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Access Other Real World Math Tasks
Search More 3 Act Math Tasks
Grade 2 [2.B1.1, 2.B1.3, 2.B2.1, 2.B2.2, 2.B2.3, 2.B2.4, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3]
Grade 3 [3.B1.5, 3.B2.1, 3.B2.3, 3.B2.7, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3]
Grade 4 [4.B2.1, 4.B2.4, 4.E2.5, 4.E2.6, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 5 [5.B1.7, 5.B2.9, 5.D1.3, 5.D1.6, 5.E2.6, 5.F1.2, 5.F1.5, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 6 [6.B2.12, 6.B2.9, Data Management and Probability - DP3, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 7 [7.B1.3, 7.B1.4, 7.B1.7, 7.B2.2, 7.B2.3, 7.C1.1, 7.C1.2, 7.C1.3, 7.C1.4, 7.D1.6, Data Management and Probability - DP3, Geometry and Spatial Sense - GS1, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 8 [8.B1.4, 8.B2.5, 8.C1.1, 8.C1.2, 8.C1.3, 8.C1.4, Data Management and Probability - DP1, Data Management and Probability - DP3, Geometry and Spatial Sense - GS2, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 9 [9.B3.5, 9.C3.1, 9.C3.2, 9.C3.3]
Kindergarten [k.15.1, k.15.10, k.15.2]
MAP4C [Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MAT1LMAT2LMBF3C [Data Management - DM1, Data Management - DM2, Geometry and Trigonometry - GT1, Geometry and Trigonometry - GT2, Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MCF3M [Exponential Functions - EF2, Quadratic Functions - QF1, Quadratic Functions - QF2, Quadratic Functions - QF3, Trigonometric Functions - TF1, Trigonometric Functions - TF3]
MCR3U [Characteristics of Functions - CF1, Characteristics of Functions - CF2, Exponential Functions - EF2, Exponential Functions - EF3, Trigonometric Functions - TF3]
MCT4C [Exponential Functions - EF1, Trigonometric Functions - TF3]
MCV4U [Derivatives and Their Applications - DA2]
MDM4U [Counting and Probability - CP2, Organization of Data For Analysis - DA2, Probability Distributions - PD1, Statistical Analysis - SA1, Statistical Analysis - SA2]
MEL4EMFM1P [Linear Relations - LR1, Linear Relations - LR2, Linear Relations - LR3, Linear Relations - LR4, Measurement and Geometry - MG1, Measurement and Geometry - MG2, Measurement and Geometry - MG3, Number Sense and Algebra - NA1, Number Sense and Algebra - NA2]
MFM2P [Measurement and Trigonometry - MT1, Measurement and Trigonometry - MT2, Measurement and Trigonometry - MT3, Modelling Linear Relations - LR1, Modelling Linear Relations - LR2, Modelling Linear Relations - LR3, Quadratic Relations in y = ax^2 + bx + c Form - QR1, Quadratic Relations in y = ax^2 + bx + c Form - QR2, Quadratic Relations in y = ax^2 + bx + c Form - QR3]
MHF4U [Characteristics of Functions - CF3, Exponential and Logarithmic Functions - EL2, Exponential and Logarithmic Functions - EL3]
MPM1D [AG3, Analytic Geometry - AG1, Analytic Geometry - AG2, LR1, LR2, LR3, MG1, MG2, MG3, NA1, Number Sense and Algebra - NA2]
MPM2D [AG1, AG2, AG3, QR2, Quadratic Relations - QR3, Quadratic Relations - QR4, T2, T3]
Functions [F-BF.1, F-BF.3, F-IF.4, F-LE.1, F-LE.2, F-LE.3, F-TF.5]
Geometry [G-C.5, G-C.8, G-C.9, G-GMD.3, G-GMD.4, G-GPE.4, G-GPE.5, G-GPE.7, G-MG.1, G-MG.2, G-SRT.11]
Grade 1 [1.NBT.4, 1.OA.1, 1.OA.6, 1.OA.A.1, 1.OA.B.3, 1.OA.B.4, 1.OA.C.5, 1.OA.C.6]
Grade 2 [2.NBT.5, 2.NBT.B.5, 2.NBT.B.8, 2.NBT.B.9, 2.OA.2, 2.OA.A.1, 2.OA.B.2]
Grade 3 [3.MD.C.5, 3.NBT.2, 3.NF.1, 3.NF.2, 3.NF.3, 3.NF.A.1, 3.OA.1, 3.OA.5, 3.OA.9]
Grade 4 [4-MD.3, 4.MD.1, 4.MD.2, 4.NBT.6, 4.NF.3, 4.NF.5, 4.NF.6, 4.OA.1, 4.OA.5]
Grade 5 [5.B1.7, 5.D1.3, 5.D1.6, 5.MD.1, 5.MD.3, 5.MD.4, 5.MD.5, 5.NBT.2, 5.NBT.3, 5.NBT.6, 5.NBT.7, 5.NF.1, 5.NF.2, 5.NF.3, 5.NF.4, 5.NF.5, 5.OA.1, 5.OA.2, 5.OA.3]
Grade 6 [6.EE.1, 6.EE.2, 6.EE.5, 6.EE.6, 6.EE.7, 6.G.1, 6.G.2, 6.NS.1, 6.NS.3, 6.NS.6, 6.NS.B.3, 6.NS.C.6, 6.NS.C.7, 6.NS.C.8, 6.RP.1, 6.RP.2, 6.RP.3, 6.RP.A.1, 6.RP.A.2, 6.RP.A.3, 6.RP.A.3.C]
Grade 7 [7.EE.3, 7.EE.4, 7.EE.A.1, 7.G.3, 7.G.4, 7.G.6, 7.NS.A.1, 7.NS.A.2, 7.RP.1, 7.RP.3, 7.RP.A.2.B, 7.RP.A.3, 7.SP.2, 7.SP.5, 7.SP.6]
Grade 8 [8.EE.1, 8.EE.5, 8.EE.6, 8.EE.7, 8.EE.8, 8.F.2, 8.F.3, 8.F.4, 8.F.5, 8.G.5, 8.G.6, 8.G.7, 8.G.9, 8.SP.1]
Grade 9Kindergarten [K.CC.A.1, K.NBT.A.1, K.OA.A.1, K.OA.A.2, K.OA.A.3]
Practice [MP.1, MP.2, MP.3, MP.4, MP.6, MP.7]
Statistics & Probability [S-ID.6, S-MD.4]












Thank you so much for this. I plan to use it in the classroom.
Thanks for stopping by! Let me know how it goes!
Thank you so much for this. I plan to use it in the classroom.
Task 2: I get a weight of 6.4 for the pen. Why the discrepancy?
I also got the weight of the pen to be 6.4 in task #2.
With Task 1: Sticky Situation, students graphed in DESMOS the two equations representing the problem, being 5x + 4y = 679 and 12x +3y = 680. The coordinates of the point of intersection of these two equations is (20.7, 143.9). However, this does not match the mass of the glue stick (being 21) and the mass of the glue bottle (145). Why the discrepancy? I’m guessing because the weight scale is calibarated to the nearest whole gram, while in actual fact the mass of the stick and the bottle the actual mass are not whole gram numbers. With that in mind, I just don’t know how students at Grade 8 level will come up with a solution to this problem. They’ve already spent a whole lesson on this problem. Comments please.
Hi My Friends,
I thiink you’ve shared a very possible explanation for why the discrepancy. This is literally a “real world problem” and that means we’re dealing with “real world problems” that often come up unintentionally. Rather than hyper-focusing on a solution coming up to exactly the nearest tenth of a gram (a very small unit of measure), allow students to make conjectures as to why there might be a discrepency.
I certainly hope that we aren’t saying “you’re off by 3 tenths of a gram, so something must be wrong with your approach” rather than viewing the big picture and allowing students to better determine if that is “close enough” to seem realistic.
Just thoughts here, but do with them what you may…