Counting Candy Sequel

No Expectations/Standards Selected

Solving Systems of Linear Equations With Context

Previously, the Counting Candy 3 Act Math Task that had students problem solving with fractions to determine how many candies each of four people should receive given the number of candies in 2/3 of the container. The Sequel extends this idea and asks students to determine how many of each colour are there using a system of linear equations.

While the original Counting Candy task may seem below the level of students who are expected to solve a system of equations, but I’d recommend doing the original task to add to the development of the question.

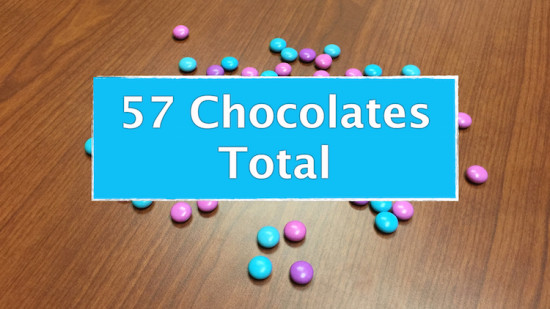
Act 1: Introducing the Problem

Act 2: Releasing Information

Supporting images:

Act 2 – Solving a Single Linear Equation Version
Not solving systems? Use this version for a single linear equation.

Supporting image for Single Linear Equation

Act 3: Watch the Solution

Act 3 – Solving a Single Linear Equation Version
Not solving systems? Use this version for a single linear equation.

Supporting Images:

Solution Exemplars and Lesson Outline:

When I deliver the Counting Candies Sequel, I typically do the Counting Candies task first. It is a very low floor task that hooks students in and gives all learners a feeling of success prior to diving into solving Systems of Linear Equations. Once that is complete, we get the kids using inquiry and prior knowledge to solve the Counting Candies Sequel. When I give this task to teachers, they typically jump straight to algebra and start building a system of equations. However, when we leave students to their own devices, you’re likely to get something simple (and likely more efficient) than a system.

Exemplar #1: Solution Using Discovery/Inquiry Approach

Here’s an exemplar of what a student might come up with prior to the introduction of systems of equations. This is a GOOD thing! We want students to build their confidence in math by proving that they can solve problems given their prior knowledge and intuition!

After discussing a solution like this, you might want to start making connections to algebra and consolidating by formalizing the idea of a system of equations and what must be done to solve it. Students have done this intuitively here, so now it could be easier for them to make that connection in the algebraic world.

Exemplar #2: Solution Using A System of Equations

Most teachers who have taught systems of equations will immediately recognize that a system will do the trick. However, in this case, it seems almost redundant to solve the problem with a system:

WOW. That was a lot of work when a student could solve it in 3 pretty basic steps.

So why would a teacher jump to a system when it could be done more efficiently using simple arithmetic/logic? Could it be that we have built the automaticity to quickly identify problems and match them with the procedural solution?

I don’t know about you, but I would much rather a ___________ (fill in with: student, employee, etc.) to select the most efficient solution for the task. Surprisingly, math doesn’t ALWAYS make things easier. However, a task like this makes it so much easier to then move to a situation where maybe the solution isn’t so easy to do without an algebraic system of equations.

Exemplar #3: Another System of Equations Exemplar

Funny enough, following a procedure like in exemplar #2 can also make things more complex if we don’t stand back and think about the most efficient place to begin. Because we have two equations with an expression of x + y, we could skip some steps and immediately isolate z:

I hope that you find this task as well as the exemplars useful when you are trying to help your students begin working with systems of linear equations. I find it very helpful and even get students solving this task in younger grades just because they can!

Download Resources:

You can access all the resources in a shared Google Drive folder here.

Or, download files individually here:

Act 1 [VIDEO]
Act 2 [VIDEO]
Act 3 [VIDEO]
Counting Candies & Sequel Slide Deck [KEYNOTE]
Images [SHARED FOLDER]
All Resources [SHARED FOLDER]

New to Using 3 Act Math Tasks?

Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!

DOWNLOAD TIP SHEET

Share With Your Learning Community:

About Kyle Pearce

I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.