Ontario Alignment By Overall Expectation
Starting a Month of Math to Celebrate Canada’s 150th Birthday
As you might have heard, 2017 marks Canada’s 150th year of Confederation and me and my Canadian friends are pretty excited about it. You can probably imagine how geeked I was when Heidi Horn-Olivito came to me with a math challenge that she and the collaborative inquiry team at Dr. David Suzuki Public School thought up around Canada’s 150th Birthday. They originally wanted to challenge our district, Greater Essex County District School Board (GECDSB) to a month of Canada 150 Math during June. However, I’ve upped the ante and I’m challenging all of Canada.
While we’ll be providing a math question and/or provocation during the entire month of June via the @Canada150Math Twitter account and #Canada150Math hashtag, this is a 3 Act Math Task taking on an Estimation180-like beginning that focuses on ratio, rate and proportional reasoning that was used to kick-off the Canada 150 Math Challenge at Dr. David Suzuki Public School on May 31st.
The context involves The Great Canadian Flag that was just installed in Windsor, Ontario at the foot of Ouellette Avenue on the waterfront of the Detroit River.
Special thanks to Jon Orr for providing very valuable feedback as I was brainstorming this task out.
Act 1: Introduce the Task
#Canada150Math Challenge for June 1st
Show students the act 1 video.
Then ask students to do a rapid write of what they notice and what they wonder. Alternatively, you might have students simply chat this out with their neighbours.
Some possible noticings and wonderings may include:
- Where is this video taken?
- How big is the flag?
- That is The Great Canadian Flag!
- When was this video taken?
- How much bigger is that flag than the one in front of our school?
- And many others…
Before settling on any wonderings to explore, I show students this video.
From the video, students are challenged to predict:
How many Mr. Pearces tall is The Great Canadian Flag?
They see me up close:
And zoomed out:
Then, I ask them to make a prediction based only on their spatial reasoning from the visual and intuition.
Once students have been given some time to think independently and then discuss with neighbours, we will share out to the group and jot down some predictions.
Act 2: Reveal Some Information
After students have stated predictions and their reasoning, I’ll show students some more information gradually.
First, I might have students predict my height:
I might give them an imagine like this one with two metre sticks next to me in order to help them get a more reasonable prediction for height:
And then, we’ll reveal my actual height and also reveal the height of The Great Canadian Flag:
After students share out their predictions and I record them on the board, you might choose to give students some more information and allow them to update their predictions such as showing how tall 10 “Mr. Pearces” (or 20) would be with the corresponding measurement.
Act 3: Reveal the Solution
And then finally revealing the act 3 video to see how many Mr. Pearces it will take to reach the height of The Great Canadian Flag.
Alternatively, you could show this image:
Fun stuff, eh?
Well, we’re not done yet!
Sequel: Which Is Taller?
#Canada150Math Challenge for June 2nd
Once students finish determining how many Mr. Pearces tall The Great Canadian Flag is, we can then give them this image to ponder:
When I ran this one by Jon Orr, he thought most students would intuitively pick the Renaissance Center. However, I opted to use this as a way to keep the floor really low to start. Interestingly, when I ran this task today at Dr. David Suzuki Public School, some of the younger elementary students did pick the flag likely based on the perspective provided in the image.
However, what we are really interested in is:
How much taller is the Renaissance Center?
In order to give students an accessible entry point, I offer up this video which gives four possibilities to choose from.
Alternatively, you can show this image: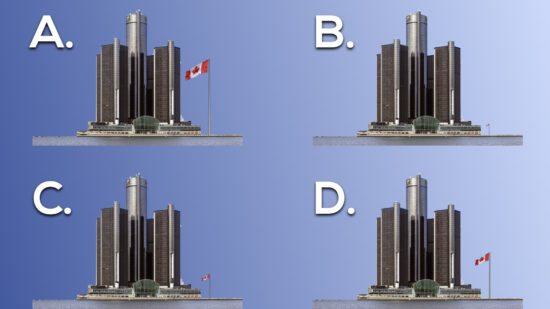
I then give students some time to discuss and strategize before taking a vote.
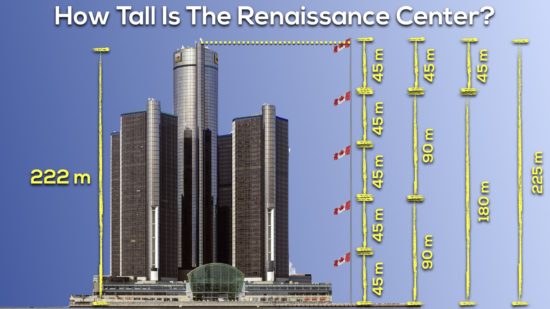
Then, we show students the true scale relationship between the height of both The Great Canadian Flag and the Renaissance Center:
Celebrate those who predicted correctly before offering up yet another challenge:
How many “Great Canadian Flags” tall is the Renaissance center?
While some students will feel like rockstars if they predict the answer to be 5, let them know that the Renaissance Center is just slightly shorter than 5 Great Canadian Flags:
And for the Grand Finale:
About how tall is the Renaissance Center in standard units?
This is a fun way to potentially lead a number talk and hopefully get kids doing some math using mental, visual or written math strategies without the use of a calculator (if possible).
Students might surprise themselves at how close they can get without resorting to punching numbers into the calculator prior to thinking it through with friendly numbers and/or mental math strategies.
Sequel #2: How Many Beach Towels?
Day 12 of the #Canada150Math Challenge – June 16th
Initially when the #Canada150Math Challenge came up as an idea from the math team at Dr. D Suzuki Public School and my colleague, Heidi Horn-Olivito, a ton of questions were generated to celebrate Canada’s 150th Birthday.
One of the questions related to The Great Canadian Flag that I came up with was:
How many t-shirts would it take to make The Great Canadian Flag?
When I ran some ideas about using The Great Canadian Flag by Jon Orr, he coincidentally came up with a question around beach towels that I thought was pretty slick and a huge step up from randomly calculating the number of T-Shirts:
So, with that, we’ve got a few images to show students and have them consider. Maybe having them read the headline from this CBC article about The Great Flag Project or showing this image:
You can do a notice/wonder or simply show this question for them:
How many beach towels would it take to cover the Great Canadian Flag?
or alternatively, the same question but using Jon’s wording:
If we all laid on beach towels, how much of us would we need to cover the flag?
You can then have them make a prediction.
For Act 2, you can share the dimensions of the Great Flag from the article as well as the dimensions of a standard beach towel.
Be sure to share out your student thinking and work on Twitter!
Well, that’s it for the first of many tasks for the #Canada150Math Challenge we’ll be promoting throughout this month to celebrate Canada’s 150th Birthday!
Be sure to check back to my blog, the GECDSB Canada150Math page and follow the @Canada150Math Twitter account and #Canada150Math hashtag to access a new math question or provocation each weekday throughout the month. We hope you’ll share photos of students engaging in Canada150Math tasks and their thinking so we can re-tweet with the rest of Canada!
New to Using 3 Act Math Tasks?
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Access Other Real World Math Tasks
Search More 3 Act Math Tasks
Grade 2 [2.B1.1, 2.B1.3, 2.B2.1, 2.B2.2, 2.B2.3, 2.B2.4, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3]
Grade 3 [3.B1.5, 3.B2.1, 3.B2.3, 3.B2.7, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3]
Grade 4 [4.B2.1, 4.B2.4, 4.E2.5, 4.E2.6, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 5 [5.B1.7, 5.B2.9, 5.D1.3, 5.D1.6, 5.E2.6, 5.F1.2, 5.F1.5, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 6 [6.B2.12, 6.B2.9, Data Management and Probability - DP3, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 7 [7.B1.3, 7.B1.4, 7.B1.7, 7.B2.2, 7.B2.3, 7.C1.1, 7.C1.2, 7.C1.3, 7.C1.4, 7.D1.6, Data Management and Probability - DP3, Geometry and Spatial Sense - GS1, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 8 [8.B1.4, 8.B2.5, 8.C1.1, 8.C1.2, 8.C1.3, 8.C1.4, Data Management and Probability - DP1, Data Management and Probability - DP3, Geometry and Spatial Sense - GS2, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 9 [9.B3.5, 9.C3.1, 9.C3.2, 9.C3.3]
Kindergarten [k.15.1, k.15.10, k.15.2]
MAP4C [Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MAT1LMAT2LMBF3C [Data Management - DM1, Data Management - DM2, Geometry and Trigonometry - GT1, Geometry and Trigonometry - GT2, Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MCF3M [Exponential Functions - EF2, Quadratic Functions - QF1, Quadratic Functions - QF2, Quadratic Functions - QF3, Trigonometric Functions - TF1, Trigonometric Functions - TF3]
MCR3U [Characteristics of Functions - CF1, Characteristics of Functions - CF2, Exponential Functions - EF2, Exponential Functions - EF3, Trigonometric Functions - TF3]
MCT4C [Exponential Functions - EF1, Trigonometric Functions - TF3]
MCV4U [Derivatives and Their Applications - DA2]
MDM4U [Counting and Probability - CP2, Organization of Data For Analysis - DA2, Probability Distributions - PD1, Statistical Analysis - SA1, Statistical Analysis - SA2]
MEL4EMFM1P [Linear Relations - LR1, Linear Relations - LR2, Linear Relations - LR3, Linear Relations - LR4, Measurement and Geometry - MG1, Measurement and Geometry - MG2, Measurement and Geometry - MG3, Number Sense and Algebra - NA1, Number Sense and Algebra - NA2]
MFM2P [Measurement and Trigonometry - MT1, Measurement and Trigonometry - MT2, Measurement and Trigonometry - MT3, Modelling Linear Relations - LR1, Modelling Linear Relations - LR2, Modelling Linear Relations - LR3, Quadratic Relations in y = ax^2 + bx + c Form - QR1, Quadratic Relations in y = ax^2 + bx + c Form - QR2, Quadratic Relations in y = ax^2 + bx + c Form - QR3]
MHF4U [Characteristics of Functions - CF3, Exponential and Logarithmic Functions - EL2, Exponential and Logarithmic Functions - EL3]
MPM1D [AG3, Analytic Geometry - AG1, Analytic Geometry - AG2, LR1, LR2, LR3, MG1, MG2, MG3, NA1, Number Sense and Algebra - NA2]
MPM2D [AG1, AG2, AG3, QR2, Quadratic Relations - QR3, Quadratic Relations - QR4, T2, T3]
Functions [F-BF.1, F-BF.3, F-IF.4, F-LE.1, F-LE.2, F-LE.3, F-TF.5]
Geometry [G-C.5, G-C.8, G-C.9, G-GMD.3, G-GMD.4, G-GPE.4, G-GPE.5, G-GPE.7, G-MG.1, G-MG.2, G-SRT.11]
Grade 1 [1.NBT.4, 1.OA.1, 1.OA.6, 1.OA.A.1, 1.OA.B.3, 1.OA.B.4, 1.OA.C.5, 1.OA.C.6]
Grade 2 [2.NBT.5, 2.NBT.B.5, 2.NBT.B.8, 2.NBT.B.9, 2.OA.2, 2.OA.A.1, 2.OA.B.2]
Grade 3 [3.MD.C.5, 3.NBT.2, 3.NF.1, 3.NF.2, 3.NF.3, 3.NF.A.1, 3.OA.1, 3.OA.5, 3.OA.9]
Grade 4 [4-MD.3, 4.MD.1, 4.MD.2, 4.NBT.6, 4.NF.3, 4.NF.5, 4.NF.6, 4.OA.1, 4.OA.5]
Grade 5 [5.B1.7, 5.D1.3, 5.D1.6, 5.MD.1, 5.MD.3, 5.MD.4, 5.MD.5, 5.NBT.2, 5.NBT.3, 5.NBT.6, 5.NBT.7, 5.NF.1, 5.NF.2, 5.NF.3, 5.NF.4, 5.NF.5, 5.OA.1, 5.OA.2, 5.OA.3]
Grade 6 [6.EE.1, 6.EE.2, 6.EE.5, 6.EE.6, 6.EE.7, 6.G.1, 6.G.2, 6.NS.1, 6.NS.3, 6.NS.6, 6.NS.B.3, 6.NS.C.6, 6.NS.C.7, 6.NS.C.8, 6.RP.1, 6.RP.2, 6.RP.3, 6.RP.A.1, 6.RP.A.2, 6.RP.A.3, 6.RP.A.3.C]
Grade 7 [7.EE.3, 7.EE.4, 7.EE.A.1, 7.G.3, 7.G.4, 7.G.6, 7.NS.A.1, 7.NS.A.2, 7.RP.1, 7.RP.3, 7.RP.A.2.B, 7.RP.A.3, 7.SP.2, 7.SP.5, 7.SP.6]
Grade 8 [8.EE.1, 8.EE.5, 8.EE.6, 8.EE.7, 8.EE.8, 8.F.2, 8.F.3, 8.F.4, 8.F.5, 8.G.5, 8.G.6, 8.G.7, 8.G.9, 8.SP.1]
Grade 9Kindergarten [K.CC.A.1, K.NBT.A.1, K.OA.A.1, K.OA.A.2, K.OA.A.3]
Practice [MP.1, MP.2, MP.3, MP.4, MP.6, MP.7]
Statistics & Probability [S-ID.6, S-MD.4]





















Trackbacks/Pingbacks