No Expectations/Standards Selected
Ontario Alignment By Overall Expectation
Introducing Angle Geometry: Constructing Related Lines
From Grade 7 to 9 in the Ontario Math Curriculum, student understanding of angle geometry is extended to include (but not limited to) the following specific expectations:
Grade 7
- constructing related lines (i.e., parallel; perpendicular; intersecting at 30º, 45º, and 60º), using angle properties and a variety of tools (e.g., compass and straight edge, protractor, dynamic geometry software) and strategies (e.g., paper folding);
Grade 8
- determine, through investigation using a variety of tools (e.g., dynamic geometry software, concrete materials, protractor) and strategies (e.g., paper folding), the angle relationships for intersecting lines and for parallel lines and transversals, and the sum of the angles of a triangle;
- solve angle-relationship problems involving triangles (e.g., finding interior angles or complementary angles), intersecting lines (e.g., finding supplementary angles or opposite angles), and parallel lines and transversals (e.g., finding alternate angles or corresponding angles);
Grade 9 Applied
- determine, through investigation using a variety of tools (e.g., dynamic geometry software, concrete materials), and describe the properties and relationships of the angles formed by parallel lines cut by a transversal, and apply the results to problems involving parallel lines (e.g., given a diagram of a rectangular gate with a supporting diagonal beam, and given the measure of one angle in the diagram, use the angle properties of triangles and parallel lines to determine the measures of the other angles in the diagram);
The expectations extend nicely through these three courses, but the topics alone can often be a bit of a drag. While I’m still going to approach finding missing angles like a “puzzle” for my students as they seem to enjoy it, I have felt pretty uninspired when trying to introduce the idea of finding what would seem to be completely random missing angles.
When I was asked by Keri K. from Kingsville PS to join her class as they prepared to introduce some angle geometry, I figured I had better put my thinking cap on to attempt making the intro to this unit of study more meaningful for students than I might have in the past. So, I thought we would try to get kids thinking about what they notice and wonder via the 3 act math task approach.
Here we go.
Act 1: Introduce the Problem
Before we started, I ask students to think about what they notice and what they wonder when they watch the following video.
I played the video a second time. I then asked students to take 60 seconds to create a list of what they noticed and wondered on a piece of paper.
Depending on the task, sometimes students nail the question you’re looking to focus on that day, but other times they won’t. Either way, we can always try to answer some of the questions they have shared and nudge them towards the question we are looking to tackle for the day.
Act 2: Give Some Details
After some good discussion, I move on to the act 2 video.
Or, here’s a screenshot:
Students are now fully aware of the question to ponder:
How big is the angle?
You can frame this as a challenge or possibly play up a story involving the need to reconstruct the railing in your home. I think I prefer posing it as more of a challenge since students have not yet been exposed to any angle theorems involving parallel lines with an intersecting transversal line.
Because this was not my own classroom, I thought I should start with a low floor and ensure students were comfortable with benchmark angles prior to moving on. So, we did a few warm-up questions in Knowledgehook Gameshow prior to attempting to tackle our main question from the video.
Here’s the gameshow I used: [play as student | view/clone as a teacher]
Note that I didn’t do the KH Gameshow prior to introducing the task because that would have got them thinking immediately about angles and the whole notice/wonder piece would probably be a dud. If your students have some knowledge of benchmark angles, then you might consider skipping the warm-up.
Paper Cutting Activity: Opposite Angles
Already on the desks of the students were bins including paper, scissors, markers, etc.
I said the following:
Friends:
Take a sheet of paper and fold it twice to create an “X” with the folds.[I held up a piece of paper and folded it over twice to create an “X”]
It doesn’t matter how wide or thin your “X” is and it will probably look different than your neighbour.
Now, take a marker, start at any angle you’d like and number the angles in order, clockwise.
[I modelled this.]
Cut out your four angles and piece them together on the desk.
Take one minute on your own to ‘play’ with the pieces. Jot down anything you notice. Do you notice any relationships?
Now, have a conversation with your neighbour. Ensure both of you have a turn to speak.
After sharing out with the group, students noticed that the sum of the angles is 360 degrees and that the opposite angles were equal. And so, the Opposite Angle Theorem (OAT) was born.
Then, I asked students to do the following:
Friends:
Take another sheet of paper and fold it twice to create two parallel lines with the folds.[I held up a piece of paper and folded it over twice.]
It doesn’t matter how far apart your parallel lines are and they may look a bit different than your neighbour.
Now, fold the paper once so a single fold cuts through both of the parallel lines any way you’d like.
Now, take a marker, start at any angle you’d like and number the angles in order, clockwise.
[I modelled this.]
Cut out your four angles and piece them together on the desk.
Take one minute on your own to ‘play’ with the pieces. Jot down anything you notice. Do you notice any relationships?
Now, have a conversation with your neighbour. Ensure both of you have a turn to speak.
Similar discoveries to the previous paper fold activity were discussed. We consolidated as a group and then determined that if we have parallel lines cut by a transversal, we basically have two “groups” of opposite angles.
Then, I showed the act 2 video again. Students were now ready to head out on their way to solve for the missing angle.
Act 3: Show the Answer
After students solved and shared out their work, we could consolidate the learning from this task via the Act 3 Video.
Or the animated gif:
If you try this out, let me know what you did differently in the comments!
New to Using 3 Act Math Tasks?
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Access Other Real World Math Tasks
Search More 3 Act Math Tasks
Grade 2 [2.B1.1, 2.B1.3, 2.B2.1, 2.B2.2, 2.B2.3, 2.B2.4, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3]
Grade 3 [3.B1.5, 3.B2.1, 3.B2.3, 3.B2.7, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3]
Grade 4 [4.B2.1, 4.B2.4, 4.E2.5, 4.E2.6, Measurement - M1, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 5 [5.B1.7, 5.B2.9, 5.D1.3, 5.D1.6, 5.E2.6, 5.F1.2, 5.F1.5, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS3, Patterning and Algebra - PA2]
Grade 6 [6.B2.12, 6.B2.9, Data Management and Probability - DP3, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 7 [7.B1.3, 7.B1.4, 7.B1.7, 7.B2.2, 7.B2.3, 7.C1.1, 7.C1.2, 7.C1.3, 7.C1.4, 7.D1.6, Data Management and Probability - DP3, Geometry and Spatial Sense - GS1, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 8 [8.B1.4, 8.B2.5, 8.C1.1, 8.C1.2, 8.C1.3, 8.C1.4, Data Management and Probability - DP1, Data Management and Probability - DP3, Geometry and Spatial Sense - GS2, Measurement - M1, Measurement - M2, Number Sense and Numeration - NS1, Number Sense and Numeration - NS2, Number Sense and Numeration - NS3, Patterning and Algebra - PA1, Patterning and Algebra - PA2]
Grade 9 [9.B3.5, 9.C3.1, 9.C3.2, 9.C3.3]
Kindergarten [k.15.1, k.15.10, k.15.2]
MAP4C [Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MAT1LMAT2LMBF3C [Data Management - DM1, Data Management - DM2, Geometry and Trigonometry - GT1, Geometry and Trigonometry - GT2, Mathematical Models - MM1, Mathematical Models - MM2, Mathematical Models - MM3]
MCF3M [Exponential Functions - EF2, Quadratic Functions - QF1, Quadratic Functions - QF2, Quadratic Functions - QF3, Trigonometric Functions - TF1, Trigonometric Functions - TF3]
MCR3U [Characteristics of Functions - CF1, Characteristics of Functions - CF2, Exponential Functions - EF2, Exponential Functions - EF3, Trigonometric Functions - TF3]
MCT4C [Exponential Functions - EF1, Trigonometric Functions - TF3]
MCV4U [Derivatives and Their Applications - DA2]
MDM4U [Counting and Probability - CP2, Organization of Data For Analysis - DA2, Probability Distributions - PD1, Statistical Analysis - SA1, Statistical Analysis - SA2]
MEL4EMFM1P [Linear Relations - LR1, Linear Relations - LR2, Linear Relations - LR3, Linear Relations - LR4, Measurement and Geometry - MG1, Measurement and Geometry - MG2, Measurement and Geometry - MG3, Number Sense and Algebra - NA1, Number Sense and Algebra - NA2]
MFM2P [Measurement and Trigonometry - MT1, Measurement and Trigonometry - MT2, Measurement and Trigonometry - MT3, Modelling Linear Relations - LR1, Modelling Linear Relations - LR2, Modelling Linear Relations - LR3, Quadratic Relations in y = ax^2 + bx + c Form - QR1, Quadratic Relations in y = ax^2 + bx + c Form - QR2, Quadratic Relations in y = ax^2 + bx + c Form - QR3]
MHF4U [Characteristics of Functions - CF3, Exponential and Logarithmic Functions - EL2, Exponential and Logarithmic Functions - EL3]
MPM1D [AG3, Analytic Geometry - AG1, Analytic Geometry - AG2, LR1, LR2, LR3, MG1, MG2, MG3, NA1, Number Sense and Algebra - NA2]
MPM2D [AG1, AG2, AG3, QR2, Quadratic Relations - QR3, Quadratic Relations - QR4, T2, T3]
Functions [F-BF.1, F-BF.3, F-IF.4, F-LE.1, F-LE.2, F-LE.3, F-TF.5]
Geometry [G-C.5, G-C.8, G-C.9, G-GMD.3, G-GMD.4, G-GPE.4, G-GPE.5, G-GPE.7, G-MG.1, G-MG.2, G-SRT.11]
Grade 1 [1.NBT.4, 1.OA.1, 1.OA.6, 1.OA.A.1, 1.OA.B.3, 1.OA.B.4, 1.OA.C.5, 1.OA.C.6]
Grade 2 [2.NBT.5, 2.NBT.B.5, 2.NBT.B.8, 2.NBT.B.9, 2.OA.2, 2.OA.A.1, 2.OA.B.2]
Grade 3 [3.MD.C.5, 3.NBT.2, 3.NF.1, 3.NF.2, 3.NF.3, 3.NF.A.1, 3.OA.1, 3.OA.5, 3.OA.9]
Grade 4 [4-MD.3, 4.MD.1, 4.MD.2, 4.NBT.6, 4.NF.3, 4.NF.5, 4.NF.6, 4.OA.1, 4.OA.5]
Grade 5 [5.B1.7, 5.D1.3, 5.D1.6, 5.MD.1, 5.MD.3, 5.MD.4, 5.MD.5, 5.NBT.2, 5.NBT.3, 5.NBT.6, 5.NBT.7, 5.NF.1, 5.NF.2, 5.NF.3, 5.NF.4, 5.NF.5, 5.OA.1, 5.OA.2, 5.OA.3]
Grade 6 [6.EE.1, 6.EE.2, 6.EE.5, 6.EE.6, 6.EE.7, 6.G.1, 6.G.2, 6.NS.1, 6.NS.3, 6.NS.6, 6.NS.B.3, 6.NS.C.6, 6.NS.C.7, 6.NS.C.8, 6.RP.1, 6.RP.2, 6.RP.3, 6.RP.A.1, 6.RP.A.2, 6.RP.A.3, 6.RP.A.3.C]
Grade 7 [7.EE.3, 7.EE.4, 7.EE.A.1, 7.G.3, 7.G.4, 7.G.6, 7.NS.A.1, 7.NS.A.2, 7.RP.1, 7.RP.3, 7.RP.A.2.B, 7.RP.A.3, 7.SP.2, 7.SP.5, 7.SP.6]
Grade 8 [8.EE.1, 8.EE.5, 8.EE.6, 8.EE.7, 8.EE.8, 8.F.2, 8.F.3, 8.F.4, 8.F.5, 8.G.5, 8.G.6, 8.G.7, 8.G.9, 8.SP.1]
Grade 9Kindergarten [K.CC.A.1, K.NBT.A.1, K.OA.A.1, K.OA.A.2, K.OA.A.3]
Practice [MP.1, MP.2, MP.3, MP.4, MP.6, MP.7]
Statistics & Probability [S-ID.6, S-MD.4]




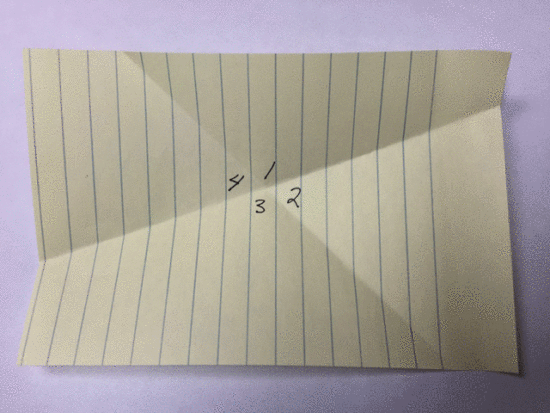


I’m trying to download the answers from your 3 act math task on Transversals, but I’m unable to. Also, do I have to create my own knowledge hook assignments?
Hey there! There are no “answers” but rather just the resources to run the task in your classroom. As for Knowledgehook, they have pre-created activities but you can also create your own custom activities.