The Orange Juice Judgement

Real World Mathematics in Proportional Reasoning & Measurement

In The Orange Juice Judgement, students will have an opportunity to utilize skills related to proportional reasoning and measurement when Mr. Pearce intends to provide the class with some orange juice to help quench the thirst of his period 1 MPM1D Principles of Mathematics, Grade 9 class.
 

Math Topics Related To This Activity:

• Proportional reasoning, specifically:
  • unit cost, and
  • setting up and solving proportions.
• measurement and volume of a cylinder.

Minds On:

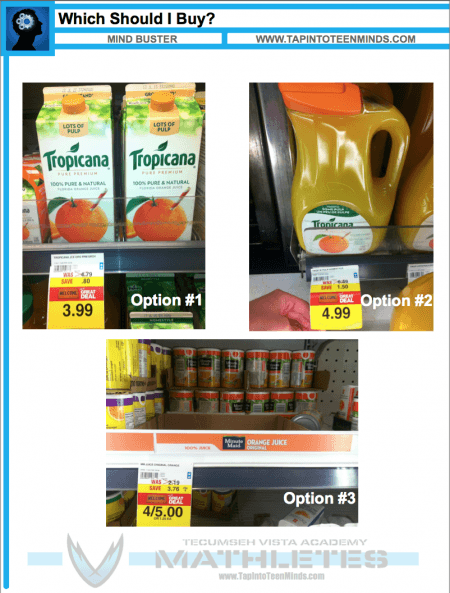
While Mr. Pearce was at the grocery store to purchase the orange juice for the class, there were many different selections of orange juice to select. Here are three of the options he could select:

 
Problem That Must Be Solved:

Which orange juice should Mr. Pearce buy?

Making Predictions:

• Which orange juice option do you predict will be cheapest? Most expensive?
• How many containers of orange juice will Mr. Pearce have to buy?
• How much do you think Mr. Pearce is going to have to spend?

Some prompts for students:

• What could we do to find the least costly orange juice?
• What information will be necessary to help us decide?

Providing More Details

Students will likely realize that they need to know the volume of each orange juice option:

 
At this point, students will likely begin finding the unit cost of each orange juice option. Some may begin to realize that while they can find the unit cost of all three options, the true unit cost of option #3 must be calculated when the added water is taken into consideration:

Mixing Instructions

Solution Exemplar Using Proportions:

Action:

Once students have determined that the concentrate orange juice option would provide the lowest unit price, we can then begin determining other important questions such as:

• How much water will we need to create enough juice for the whole class?
• How many juice containers will we need to hold it?
• What would you classify as a typical “serving size” of orange juice?
• How much juice will each plastic cup hold?

How Much Can Each Cup Hold?

If you have cups for your students to use, they can begin measuring to determine how much each will hold.

Asking students what information is important would be a good discussion to have in order to ensure they understand how to calculate the volume of a cylinder using the area of the base x height.

If you do not have cups on hand, you can use the following as a replacement:

Are Your Students Up For A Challenge?

If you purposely select a cup that holds more orange juice than what you would like each student to have, you could have students try to devise a strategy to determine at what point you should stop pouring.

For example, the cups we used today can hold approximately 473 ml, but I wanted each student to only receive one serving (250 ml). Your students may use a variety of strategies to try to make this calculation, or if you are in an advanced functions or calculus course, they may be able to narrow it down exactly.

Consolidation:

There are many consolidation options available for you to consider. However, if you are teaching in an intermediate classroom, you might want to consider the linear relationship between the amount of water and concentrate used to create the orange juice. I find that once students realize that proportional reasoning is connected directly with linear relationships, they develop a deeper understanding and feel more confident about the problem solving they engage in daily.

Download a PDF Worksheet to Help Guide Your Lesson:

Suitable for the Following Ontario Mathematics Curriculum Courses:

• Grade 6
• Grade 7
• Grade 8
• Grade 9
  • MAT1L – Locally Developed Math
  • MFM1P – Foundations of Mathematics
  • MPM1D – Principles of Mathematics

New to Using 3 Act Math Tasks?

Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!

DOWNLOAD TIP SHEET

About Kyle Pearce

I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.

• Follow
• Follow
• Follow
• Follow
• Follow
• Follow

Access Other Real World Math Tasks

Search More 3 Act Math Tasks