A Weekly Summary of My Math Classroom
October 5th to 9th, 2015
After three days out of the classroom, it felt great to be back working on some math with my students. This week, I wanted to explicitly discuss the difference between direct and partial variation linear relations and then start moving towards solving multi-step linear relations that involve collecting like terms, distribution and (hopefully) equations involving fractions. Let’s see how well we did meeting those goals.
Day #19 – Monday October 5th, 2015
Direct & Partial Variation With Flaps! and Crazy Taxi
Although we have been looking at linear patterning on and off since the first day of school, most have been proportional where the initial value (or y-intercept) is 0. Since the first day, I have been asking students to identify the equation in order to find the value of the dependent when the value of the independent is large (like figure number 47) or visa versa. Occasionally, I have snuck in a linear pattern that is not proportional by changing the initial value to something other than 0 (like Placing Toothpicks Part 3). This occasional “sneakery” is because I wanted to make it easy and natural for students to tackle this learning goal:
- LR2.04 – I can compare the properties of direct variation and partial variation in applications, and identify the initial value when described in words, represented as a table, a graph, or an equation.
In Ontario, we refer to a direct variation as a linear relationship with an initial value of zero and a partial variation as a linear relationship with an initial value not equal to zero. Since we have tackled many different linear relations with descriptions, tables, and graphs, it makes sense that students are ready to tackle this not so complex learning goal. Something to note is that we have not explicitly started with the graph of a linear relation and found the other representations. We will be inching towards starting with a graphical representation in the coming weeks.
In order to get kids thinking right off the bat, my Minds On involves jumping straight into Jon Orr’s Flaps! 3 Act Math Task. I show them the act 1 video to get them thinking:
Can’t see the video? Click here.
I ask students to talk to their groups about what questions they have about the slow-motion video. Ultimately, we are hoping to get somewhere close to this question:
How fast are the hummingbird’s wings flapping?
Usually, I have students individually make their predictions and share out. Today, I had students make their own prediction, discuss with their group, and compromise to make a “group prediction” they could share out as a team. It was interesting because now students felt like they had to better justify their own prediction in order for the group to agree on a number closer to their individual prediction. I’ll definitely try this again in the future.
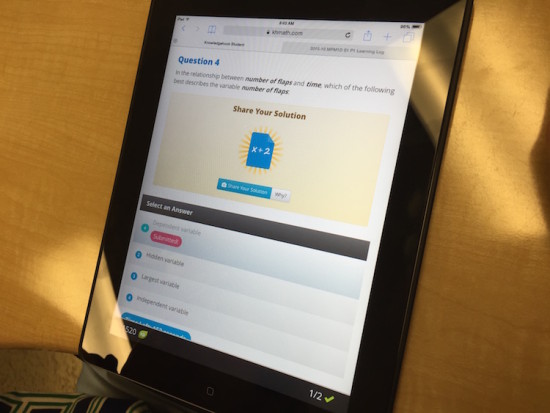
After sharing out the group predictions, I showed students Act 2 of the Flaps! task and then started a Knowledgehook Custom Gameshow that I made to use for students to interact throughout the tasks for that day. Here’s a couple of the questions from the gameshow:
Keeping with the theme of spiralling the course, I always want to make sure we don’t take for granted that things like identifying independent and dependent variables are common knowledge. So, let’s keep bringing them back throughout the year:
If you’ve been reading my other Week In Review posts, you’ve probably picked up on the fact that I haven’t been delivering a traditional lesson with a lecture and note. I have been trying to introduce new concepts as tasks are being delivered rather than formally defining these new concepts, giving examples, and then trying to have students use the knowledge throughout a task. By flipping this idea on its head, I get into the task, sort of have the students prove to themselves that they can solve any problem that is put in front of them using intuition and prior knowledge, then help them define, identify and consolidate what skills they were actually using to do the work. During the Custom Gameshow, I formally introduce the concept of direct and partial variation:
Students have been encountering direct and partial variation since the beginning of the year, yet we never had a label on it. Now, I’m hoping to start using this terminology moving forward. Some other terms we are starting to use more frequently, even though I haven’t formally introduced them in the traditional sense is initial value and rate of change:
The task (and custom gameshow) go on to extend the concepts here by having them identify an equation that models this relation, determining the number of flaps in 5 minutes, and finding how long it would take the hummingbird to flap its wings 1 million times.
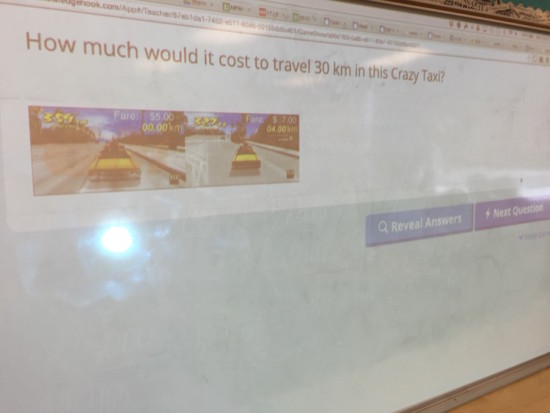
Then, I toss them another contextual task from Jon Orr called Crazy Taxi with the intention of giving students an example of partial variation. Here’s the first act:
Can’t see the video? Click here.
After travelling a few kilometres, the game fast forwards and asks the viewer to determine:
How much would it cost to travel 30 km?
Some key information include the initial value of $5 on the meter before the taxi begins moving and a rate of change of $0.50 per kilometre travelled.
Even though I created math task template files in PDF form in the past for Flaps! and Crazy Taxi, I let the Knowledgehook Custom Gameshow do all of that work. I still have the urge to give a template for everything we do, but often times, that sort of “tells” the students that they must do a certain series of things in order to solve the problem. I want them to truly make the call on how they go about things. I have enough structure on my Tuesday Assessments, I figure.
With both of these tasks and the custom gameshow, this brought us to the end of class. Tomorrow, it is Assessment Day!
Day #20 – Tuesday October 6th, 2015
Assessment #4 – Rockin’ 7 Learning Goals
Here’s the learning goal lineup for Assessment #4:
- LR2.02 – I can construct tables of values, scatter plots, and lines or curves of best fit as appropriate, using a variety of tools for linearly related and non-linearly related data collected from a variety of sources.
- LR1.04 – I can describe trends and relationships observed in data, make inferences from data, compare the inferences with hypotheses about the data, and explain any differences between the inferences and the hypotheses.
- LR2.04 – I can compare the properties of direct variation and partial variation in applications, and identify the initial value when described in words, represented as a table, a graph, or an equation.
- NA2.07 – I can solve first-degree equations, including equations with fractional coefficients, using a variety of tools and strategies.
- LR1.01 – I can interpret the meanings of points on scatter plots or graphs that represent linear relations, including scatter plots or graphs in more than one quadrant.
- LR3.01 – I can determine values of a linear relation by using a table of values, by using the equation of the relation, and by interpolating or extrapolating from the graph of the relation.
- MG3.01 – I can determine, through investigation using a variety of tools and describe the properties and relationships of the interior and exterior angles of triangles, quadrilaterals, and other polygons, and apply the results to problems involving the angles of polygons.
As usual, we aren’t trying to completely assess each learning goal in its entirety. Because we are spiralling the course, we are slowly digging deeper and deeper through each expectation with the hopes that student depth of knowledge will increase each time.
Overall, the overwhelming majority of the class is right on where I would hope they would be. We do have 3 students who did struggle in a couple small areas (mixing up independent/dependent variables, uncertainty with creating an equation, etc.) but those issues can now be tackled on an individual basis prior to the start of class with a little one-on-one guidance.
Feel free to snipe the assessment below:
Day #21 – Wednesday October 7th, 2015
Number Sense and Algebra – Solving Linear Equations
The grade 9 academic course has three expectations related specifically to solving linear equations:
- NA2.07 – solve first-degree equations, including equations with fractional coefficients, using a variety of tools (e.g., computer algebra systems, paper and pencil) and strategies (e.g., the balance analogy, algebraic strategies);
- NA2.08 – rearrange formulas involving variables in the first degree, with and without substitution (e.g., in analytic geometry, in measurement) (Sample problem: A circular garden has a circumference of 30 m. What is the length of a straight path that goes through the centre of this garden?);
- NA2.09 – solve problems that can be modelled with first-degree equations, and compare algebraic methods to other solution methods (Sample problem: Solve the following problem in more than one way: Jonah is involved in a walkathon. His goal is to walk 25 km. He begins at 9:00 a.m. and walks at a steady rate of 4 km/h. How many kilometres does he still have left to walk at 1:15 p.m. if he is to achieve his goal?).
Thus far in the course, I have had students creating direct variation (or one-step equations) quite routinely and I’ve slowly been adding in partial variation (two-step equations). Almost all students can intuitively solve these two linear equations and many in that group can also do this using opposite operations, which I have not explicitly taught. Great start, for sure. You’ll note that the first expectation involves solving first-degree equations including fractional coefficients, which can be interpreted in many different ways. I’m going to stay away from the fractional coefficients equations until we get some good confidence under our belts. I plan to tackle the second expectation a little later in the course, while continuing to hit the third expectation as we do our daily contextual tasks.
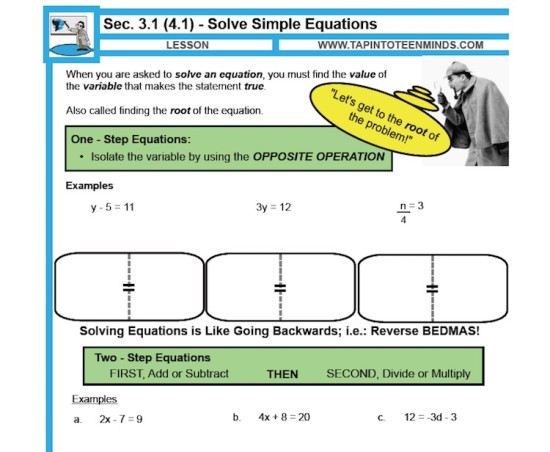
In the past, I would jump straight into rules of solving equations including the concept of opposite operations. Actually, my first “day” of solving equations had a note that looked like this:
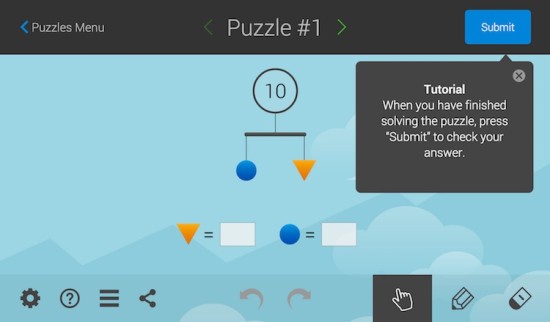
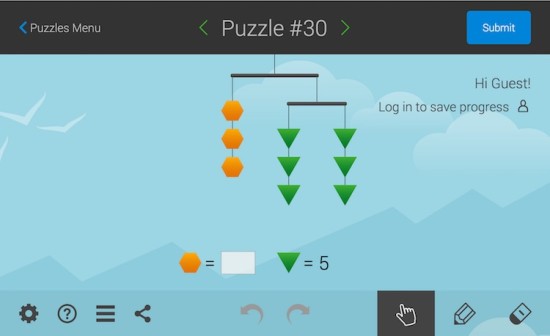
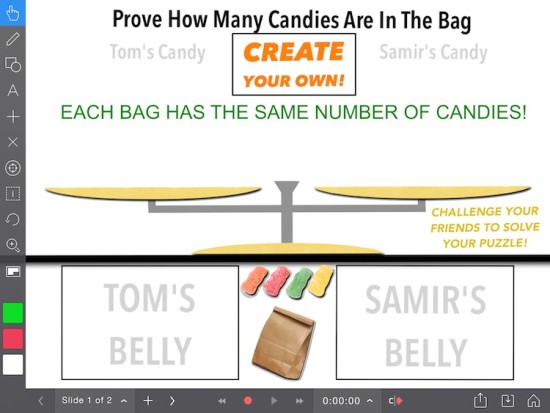
Now, along with attacking simple equations intuitively using trial and error when they come up, I try to give students different equation puzzles to work with that make them think. The puzzles I used today were SolveMe Mobiles. Students are given a puzzle consisting of different shapes that hang in balance like the items hanging from a mobile over a baby’s bed. Here’s the first one this free website serves up:
A pretty easy place to start, in my opinion. I start the kids off by having them complete the first puzzle without any guidance. As is usual when I have the students start something without any sort of detailed instructions, it seems that the strongest students are most vocal about their initial confusion with the task. I hear a lot of “what the heck are we supposed to do?” or “what is this?” and “I have no idea what I’m doing.” This is perfect, because I want my strong students to get used to the feeling of not always knowing the answer immediately. My hypothesis is that my strong students have been grouped this way because they are really good at following steps and procedures. When I don’t give them explicit steps and procedures, they start to get a bit squirmy and what I perceive to be a fixed mindset emerges. In this case, it doesn’t take long for the entire class to “get the point” of the SolveMe Mobiles. I gave them about 25 minutes to work through problems after they created a free account to track their progress.
It didn’t take long for much of the class to be up to Puzzle #30 with some students making it even farther than that.
Great classroom discussion was taking place as some students got stuck at different parts of their learning journey. I encouraged them to talk it out and try to find other ways to represent the situation (hoping for some algebra to pop up).
At this point, I stopped the class and we took one of the SolveMe Mobile puzzles and explicitly represented the puzzles as equations. First, using the shapes in the puzzle and then eventually, using variables.
So for example, this SolveMe Mobile:
…would be represented as:
hexagon + hexagon + hexagon = triangle + triangle + triangle + triangle + triangle + triangle
When a student says “do I really have to write it out like that?” I immediately ask them for an easier way. Doesn’t take long before we see stuff like this:
3 hexagons = 6 triangles
or
3h = 6t
And since we know that a triangle = 5, then:
3h = 6(5)
3h = 30and thus, h = 10.
At this point, we went to some “puzzles” that were given to them algebraically instead of visually, like the SolveMe Mobiles. We did this through gameshow and I asked students to upload their solutions so we could discuss potential strategies that might be useful for others to see. Here’s the gameshow I used:
Students made the transition fairly easily from the SolveMe Mobiles to straight algebra. I suggested that they draw it out as a SolveMe Mobile if it would help them organize their thoughts.
I had a stack of my old “Pearce Pence” currency I created on my desk and some students had asked for some. Here’s what I got in some of the Gameshow Solutions:
Pretty slick, those kiddies!
Day #22 – Thursday October 8th, 2015
Solving Linear Equations With Sour Patch Kids & Explain Everything
I was pleasantly surprised with how well my students took to solving equations algebraically last day. I often hear from teachers that there just “isn’t enough time” to include manipulatives and investigations that allow students to discover new math concepts and construct their own understanding. This thinking is 100% accurate if there are no plans to adjust the remainder of a lesson. For example, if I was unwilling to ditch my traditional note where students would copy the steps and then engage them in some examples – I mean, students would sit passively while I did the examples – then I would definitely run out of time. However, by approaching my lesson as an interactive experience that is student-centred rather than teacher-centred, my lesson is no longer something that my students have “done to them”. To follow up the activity from yesterday, I wanted to make sure my students didn’t believe that the SolveMe Mobile thing was just some sort of scam to sucker them into thinking equations were fun. So, today, I wanted to give them an interactive way to continue the idea of equations requiring balance.
Here’s what I showed them:
Can’t see the video? Click here.
Next, I had students download the first of three Explain Everything project files for iOS I had created to complement the sour patch kids equation analogy in the first video clip above. Here’s what the first slide in the file looks like:
The goal of the Explain Everything file is to allow students to intuitively solve the equation. What I typically expect is to see something like this take place:
Can’t see the video? Click here.
Students then move to the next three tasks in the Explain Everything file that look like the following:
Task #2:
Check out a sample solution:
Can’t see the video? Click here.
Task #3:
Check out a sample solution:
Can’t see the video? Click here.
Task #4:
Check out a sample solution:
Can’t see the video? Click here.
You can download the first Explain Everything Project File below:
Although the expectations of this course do not involve solving systems of linear equations algebraically, I always try to stretch the limits when possible. With the Sour Patch Kids tasks leveraging student intuition, it seems logical that students might be able to extend their thinking to a system of equations. In a second Explain Everything file, I give students the following two tasks:
I hope students can use their problem solving skills to come up with a solution. Here’s a possible approach:
Can’t see the video? Click here.
Here’s the second task:
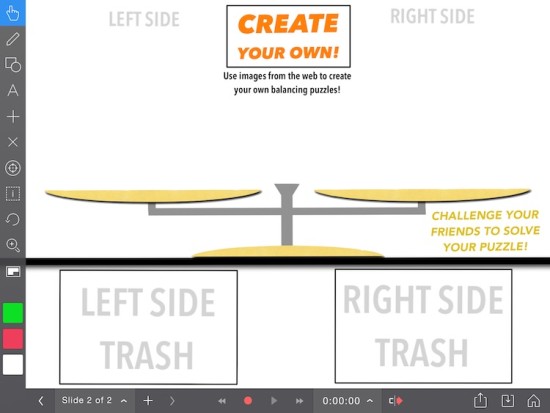
And finally, if there is time, students can download the third Explain Everything file to create their own tasks using sour patch kids as well as other items they find on the internet:
Day #23 – Friday October 9th, 2015
Sneaking In Distribution Into Solving Equations
I was pretty psyched to keep on the solving equations train and begin sneaking in distribution into the process. Not long after arriving at school in the morning I learned that half of my class would be gone on a field trip for the day. DOH! Oh well, I still went on with the lesson for the most part, as we will be spiralling back to this content later in the semester anyway.
The Minds On today was SolveMe Mobile Puzzle #71. My challenge to my students was to solve for the values of each shape in any way they wanted, but then to attempt modelling the puzzle algebraically. Students struggled to do this as I think they thought it was more complex than it really was. They could all solve it, but most were intimidated when it came to representing with algebra. Here’s a silent solution I created to share with them after students shared their solutions:
Can’t see the video? Click here.
After that, I asked students to solve the following equation:
4x + 10 = 90
After sharing out their strategies, I offered another possible way to look at solving an equation that students found helpful:
Can’t see the video? Click here.
Then, it was on to challenging the class with some tasks via the Knowledgehook Custom Gameshow below:
Can’t see the gameshow? Check it out here.
When we got to the third question, some students were stumped trying to figure out what they needed to do:
Find the root of the equation:
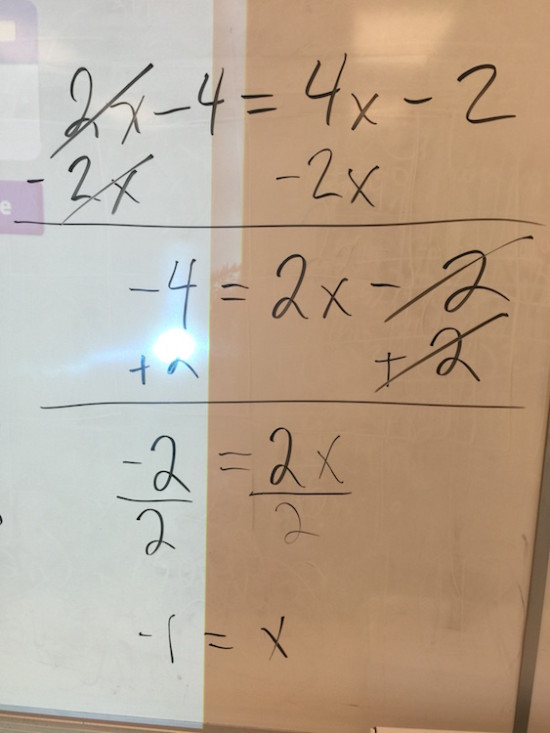
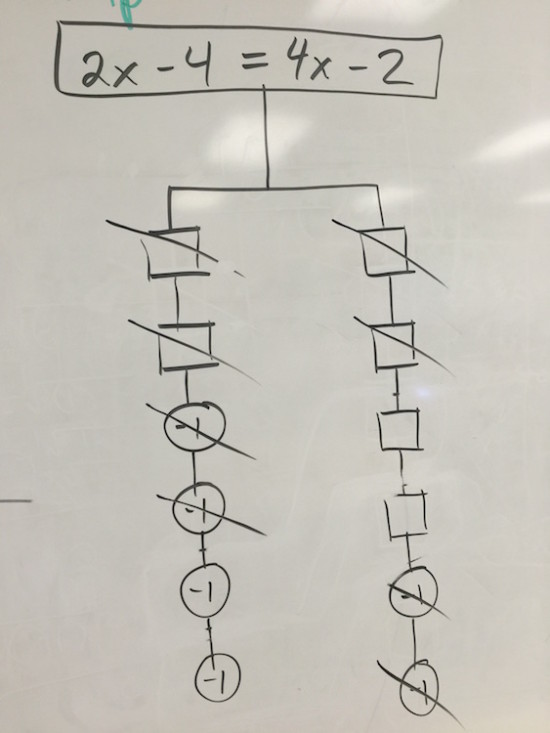
2(x – 2) = 4x – 2
Note: Think of “root” like getting to the “root” of the problem or the “SOLUTION”.
Interesting enough, most students were struggling with “BEDMAS” and the idea that they had to do something inside the brackets first. We had a great chat about why just remembering rules in math can be cause for more confusion than help.
Here’s the crash course on the distributive property that we looked at on the fly:
I gave students a bit more time to work out a solution and then suggested that maybe they try to draw their own SolveMe Mobile to help them organize their thoughts:
Finally, we consolidated the problem using algebra:
Overall, it was a fun class with some great learning moments. We definitely have more work to do on distribution and how it applies to solving equations, but I know it will come in time.
That’s it for this week! Looking forward to heading into a four-day week with the Canadian Thanksgiving Holiday on Monday. Enjoy the weekend!
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog