Check out a recent talk I gave in regards to the two groups of students I used to see forming in my math classroom each year or jump to a written summary:
When I was in school, I can remember a distinct lesson framework that I could recognize in most every math course:
- Take up homework;
- Learn New Definitions, Formulae, Procedures/Algorithms;
- Do a bunch of examples; and,
- Do a bunch of homework problems.
It seems only natural that teachers would likely deliver the math curriculum in a way familiar to them such as the way they were taught.
If we open a textbook, it won’t take long to figure out that many of them follow a similar format. More recent releases also tend to include an investigation or activity to try and address the inquiry/discovery requirements of many curriculum expectations, but the activities are written in a series of steps and without much to pique student curiosity.
Because much of my teaching looked something like what I’ve described above for the first 8 years of my career, I noticed that there were two groups of students forming in my classroom: those who are good at math and those who are not. Even though nobody said it, most students would probably identify themselves as being in one of those two groups if asked by a teacher, parent or friend.
Good at Math vs. Not Good at Math
I would typically consider students in the Good at Math group those who know:
- terminology, definitions, math language; and,
- procedures, steps, algorithms.
While students in the Not Good at Math group tend to have neither.
I need to be really careful here because I don’t think we intentionally aim for students to only be proficient in these areas, but it would seem that most math classrooms tend to assess based primarily on these particular skills.
Have We Named The Two Groups Accurately?
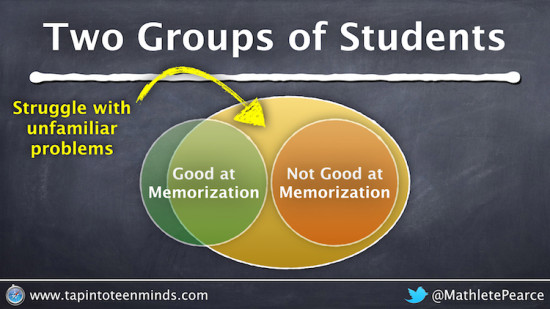
Digging deeper here, I feel as though what many math classrooms are really assessing are those students who are Good at Memorization and those who are Not Good at Memorization.
I know that there are some folks out there who really deeply understood the math when they were learning it in high school, but I was one of the many who learned to play the memorization game early and played it well. Students in the Not Good at Memorization group are typically those who are unable OR unwilling to play that same game.
My thinking here is that if you’ve ever thought that studying the night before a test to be successful in math class was the difference for some of your students, then maybe the same two groups have formed in your own classroom. Only recently have I realized that if a student cannot come into my classroom and problem solve without being notified (i.e.: told to cram the night before), then they may not really know what they’re doing and are unlikely to retain whatever knowledge they have familiarized themselves with for use later.
There IS Something In Common…
While it would appear that these groups are completely independent of each other, there is something that most students in both of these groups have in common. In my experience, most students in my classroom tend to struggle with problems that are unfamiliar.
I would tend to create assessments with problems that looked fairly similar to those we had explored throughout the unit and then toss one or two “challenging” problems at the end. When I really thought about it, the problems that I had selected to supposedly challenge my students were actually problems that didn’t follow a predictable series of steps or procedures. Essentially, they were problems that students could not memorize from their notes and thus could not manage to solve based purely on familiarity.
Fair vs. Unfair
Over the years, I have had some students claim that I was being unfair (or insert a variety of other expletive adjectives here) because I had not “taught” them how to do these problems. For quite some time I thought that maybe the students were right. If I clearly set the rules of the game as “memorization” for the majority of my assessments, then is it fair for me to change the rules of the game with 2 minutes left in the 4th quarter?
Students Might Regret Saying Anything At All…
So I agree that it is unfair to switch the rules late in the game, but also think that solving unfamiliar problems is what math is really all about. Unfortunately for my students, I am now trying to make my assessments more about problem solving rather than reproducing the steps, procedures and algorithms. Don’t get me wrong, I still need students to meet the expectations of the course, but I am trying to emphasize as many unique situations as possible to avoid students falling back on familiarity and “cramming” to assist with retention issues we commonly see over the mathematics learning continuum.
This semester, I have begun assessing my students each Tuesday and the questions relate to any learning goal we have studied previously in the course. Students are not warned what learning goals will be addressed as I want to identify where students are and where we need to improve. If a student struggles on a learning goal, it is indicated in their Skill Evidence Record and they are invited to re-address that learning goal when they are ready.
My hopes are that making some changes to my assessment practices as well as continuing to make tasks contextual, visual and concrete while also promoting the natural interconnectedness of mathematics will help me redefine what it means to be “good” at mathematics and to also maximize the number of students that can join that group when ready.
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog








I remember realizing that the reason I am “good at math” has much, much less to do with innate abilities or supportive parents than it did that a couple of math teachers at important points did *not* teach with this framework, but prodded us to think, think, think. It did *not* come naturally to me and I’d have been perfectly happy memorizing.
I credit Apollo 13 and Sputnik…