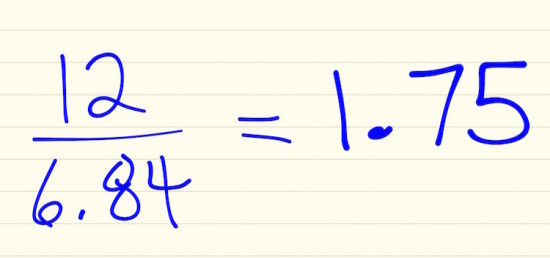An Example of Tricks and Quick Fixes Leading to a Dead End
Recently, my students were just starting their weekly assessment that interleaves/spirals our math learning goals from the year. The first problem was taken directly from an EQAO Standardized Test open response release question about unit rate:
My students have been working with ratios, rates, and proportional reasoning delivered in various contextual problems throughout the year including some unit rate problems sprinkled in. As soon as my students began solving this problem, they went straight for the strategy that they’ve likely been using since grade 6 and the strategy that I used to teach for years – division. While division does work, it is only useful when there is an understanding of “why” and I find that most struggling students (and even some strong students) are unsure of that “why”.
Here’s what I witnessed most students doing at their desks:
This is a fairly common mistake I see often when students are dealing with unit rate and comparing the best deal. The worst part is that it isn’t even a mistake at all – students can use this information to solve the problem. The issue here is that students aren’t sure what the result represents relative to the problem. What students have found is the number of oranges you can purchase for $1, which is definitely a unit rate! However, most students believe what they have found is the cost per 1 orange.
Why The Struggle?
In Ontario, students in grade 9 applied have difficulty using proportional reasoning skills and I can understand why. Proportional Reasoning is one of five strands in the Ontario Math Curriculum and a common trend I have noticed is that once it is completed, it is not intentionally addressed with other strands throughout the school year. Textbooks commonly silo topics into sections and units to suit the organizational needs of the teacher, while hurting the learner in the process. It is also common to think that re-introducing topics will derail the entire lesson that was intended to introduce a new concept.
Intentionally Derail Your Lesson As Often As Possible!
Only recently have I intentionally been spiralling content to re-introduce concepts that students haven’t used recently. This definitely does do a bit of derailing, but if that is the case, doesn’t it mean that students do not have a deep understanding of the concepts? Rather than avoiding topics that students struggle with like fractions, proportions, or calculating percentages, why not show students how all of these topics are actually interconnected? By avoiding the use of these seemingly difficult concepts whenever possible and substituting their use with tricks, rules, and algorithms, students are sure to hit a wall at some point.
Using Unit Rates As a Proportion
Using division alone to find unit rate is a trick that can cause problems like I witnessed in my classroom. This does not mean that students are discouraged from using division, however if they cannot explain why they are doing what they are doing, then a red flag goes up. Rather than simply having them divide because “that’s how you do it”, why not build a deeper conceptual understanding and also gain some practice working with proportions at the same time? What students have ultimately done in the example above (without knowing it) is this:
Digging deeper here, if we think ahead to graphing relationships with independent and dependent variables, we can see that the student has opted to use the independent variable in the numerator. When we get into rates of change and slope of linear relations, students will need to find the difference in the dependent over the difference in the independent. It might be beneficial to help students make this connection early when working with rates to avoid this misconception altogether.
By focusing on identifying the independent and dependent variables, students can determine that we are likely more interested in how much (dependent) per 1 orange (independent) than the other way around.
Using proportions on a regular basis for direct variation linear relationships not only strengthens student ability to work with proportions, but also sets them up for success when they begin finding unknowns using a table, graph, and equations. Let’s not forget that we are ultimately working with fractions as well; something I think all students could benefit from.
I will also mention that using a proportion should be more than cross-multiplication. Similar problems that prompted me to write this post when dealing with unit rate will also come up when students are instructed to multiply across an equal sign and divide. Again, I did it for the majority of my career, but I now realize that this is only a trick that will be forgotten or butchered in the future.
What this post ultimately means for us as math teachers is that our job will be more difficult. For years, I depended on tricks to make math easy for students and was always considered a “good teacher” because of it. Unfortunately, what I was really doing was making students believe that they were good at math when they were really just good at remembering my tricks and catchy ways of teaching them.
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog