Moving Away From Memorization and Toward Understanding
I must admit: I have never been a big fan of algebra tiles.
Coming from the secondary side of things, I think that most of us high school math teachers probably focus on the algebraic representation of concepts we teach. In a perfect world, students come into secondary school with a firm grasp of number sense and numeration. I mean, it’s in the elementary curriculum, right?
Unfortunately, we don’t live in a perfect world. Many students are coming to us without a firm understanding of the mathematics we expect them to use in our classes. Wait a second, my elementary educator friends; don’t go scrolling vigorously to the comment section to rip my head off for pointing the finger at you. It’s not your fault! These same students likely came into your class without a deep understanding of the course content from the previous grade as well. You might even be trying to do us secondary folk a favour by pushing more written algebra on your students and putting away the concrete math manipulatives.
While I think we are all trying to fight the same battle, I think we may have gone about it all wrong.
Teaching Students With a Blank Mathematical Canvas
Over my career, I have had the opportunity to help (or hurt) over a thousand students in their mathematics journey. With each new semester, about 90 new students would come in the door and leave 89 school days later. The more time I spend with my elementary and secondary math colleagues in the Grade 7-10 Middle Years Math Collaborative Inquiry Project, the more I realize that we are all experiencing the same struggles as math teachers in some way, shape or form. Having the opportunity to engage in deep discussions daily with @JustinLevack from LearnBlended.com and different groups of teachers from 29 different schools in my district, we are identifying a common student learning need that is difficult to address: math content retention. On a regular basis, intermediate teachers are together discussing the urgent student learning needs in their classrooms and the student inability to retain information from year-to-year has us all scratching our heads.
Memorize Doesn’t Mean Conceptualize
Analyzing my own classroom experiences, it seems that students who have a difficult time memorizing the “rules” of math seem to struggle the most. Students achieving at high levels typically can memorize steps, recognize when those steps should be applied and fire off a working solution. I’m now starting to believe that most students simply attempt to memorize rather than visualize and understand because many times, the understanding can be more difficult than the memorizing. Many of these “excellent math students” are nothing more than excellent at regurgitating information that they have committed to memory. Why I feel so strongly about this is because of the questions you’ll often get from your stronger students when you ask them to apply their thinking on an assessment using a question that is unfamiliar to them. Often times, students will claim “you never taught this” or “we’ve never seen this before.” My usual response is: “I hope you haven’t seen the question before! Otherwise, I’ll need to get more creative when making the test!”
The part that concerns me the most with this problem is that we haven’t even discussed the struggles that students in the middle or at the bottom of the class experience.
Rules, Steps, Formulae, Shortcuts: Helping or Hurting?
It seems that we as math teachers have always tried to find creative ways to help students be successful in math. After all, we DO want our students to succeed and enjoy their time with us while they are at it. For the past eight years I have been creatively devising tricks, rhymes, memory pegs and all kinds of other tactics to help students have success in math. However, the more I think about it, the more I wonder if I was simply helping them get through without gaining that deep conceptual understanding. Memories of math class for most would likely consist of memorizing rules, steps, the formula, and shortcuts to get the job done, but how many of us can honestly say that we really understood what we were doing and why we were doing it? I know I can’t.
Students Need to See It to Believe (…and remember) It!
When I learned about Dan Meyer and his 3 Act Math Tasks, I was psyched to start bringing the real world into my classroom. This was a great start to addressing proportional reasoning and getting kids to really think about the problem, but I still found more abstract concepts involving algebraic reasoning to be a struggle. I have finally invested some serious time into better understanding algebra tiles and how I might be able to leverage their use in my classroom. For what seemed to be simple manipulatives that could only be useful for very basic mathematical concepts like adding and subtracting integers, I am seeing some great opportunities to help students visualize the algebraic portions of my grade 9 course that they would otherwise struggle with. My prediction is that if I can help students break down as many concepts into visuals with algebra tiles or other manipulatives, then they will not only be able to apply the concepts now, but their deepened understanding will promote the retention of this learning for a longer period of time.
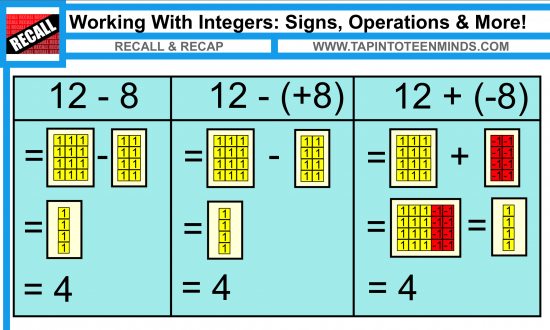
12 – 8 = 12 – (+8) = 12 + (-8)
A perfect example of this lack of understanding and inability to retain concepts from one year to the next just came up this past week. A very bright student who aced the last test in my grade 9 academic course was having a hard time accepting that 12 – 8 and 12 + (-8) were equivalent. I’d like to preface this by saying that I love when students will challenge concepts in math rather than simply accepting them as true; this is probably why she excels in her academics. Her claim was:
“12 subtract 8 is not the same as 12 plus negative 8. A subtraction sign and negative sign are different.”
After a class discussion regarding subtraction typically being used for use as an operator (i.e.: subtracting two numbers) and negative being used for representing the sign of an integer, she still didn’t seem convinced. In Ontario, integers are introduced in grade 7 and while students revisit the use of integers in grade 8 as a specific expectation, there is still a discomfort when they appear throughout the grade 9 course. Most students memorize rules and/or memorize how to punch them into the calculator to survive, but is this really helping them?
Since I have been using algebra tiles all unit to help students see collecting like terms, understand what polynomials, coefficients, variables, constants and the degree of a term are, I figured I’d try to make the explanation visual for her and the rest of the class:
My discussion with most teachers surrounding algebra tiles suggests that students do not like algebra tiles. However, I am curious if they were used early and often, whether students would develop the understanding and refrain from kicking and screaming. So far, my students have endured the algebra tiles, but I have noticed that I am getting many more questions that challenge some of the concepts we are introducing. I’d like to think that this means students are thinking more critically to make challenging a possibility. It is quite possible that my students in the past had little understanding and thus could not challenge anything presented in class.
Are you using algebra tiles? How often do you use them and for what topics? I plan to continue using them where ever I can and will share the resources and results with you!
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog


I am an elementary school math teacher who has been using Hands-On Equations for many years, and believe they are even easier to work with when introducing the addition and subtraction integers. If the kids you get had that experience in elementary school you would save lots of classroom hours.
Totally agree with you there! I’m pretty much starting from scratch with the algebra tiles right now, but I can see the benefits through the way students can visualize the math we are solving. Will definitely continue posting content to the blog to keep you updated!
It occurred to me looking at your picture why I’ve never liked algebra tiles, and I wondered if it was *my* comfort level with symbols and utter clumsiness with physical things … but no, I think it’s because they’re still “x and y.” I suspect you know that the ‘middle and bottom’ that you’re concerned about fell off the math train somewhere around multiplication — and they simply *do not* conceptually connect arrays or rows & columns (especially without even grid lines) with multiplication. So — algebra tiles are even more complicated than the rules of algebra. (I’ve also been working this week with a lady who really, really struggles with spatial stuff … so graphing lines is a nightmare because if there are two coordinates, she really wants to make two points…)
I’m thinking that a cool way to make this a “wide and/or deep” lesson would be to start with numbers (as you did with those negatives). Show those same relationships… start with the chips and making arrays.
(I like Hands-On Equations, too, especially for the concept that “=” doesn’t mean “the thing before the answer.” (http://msan.wceruw.org/research/SERP%20Misconceptions-Worked%20Examples%20Research%20Brief.pdf )
…