Unit of Study:
Unit 5 - Linear RelationsMFM1P Specific Expectations
The math help provided for MFM1P Grade 9 Applied will address the following specific expectations:LR3.01 - - determine, through investigation, that the rate of change of a linear relation can be found by choosing any two points on the line that represents the relation, finding the vertical change between the points (i.e., the rise) and the horizontal change between the points (i.e., the run), and writing the ratio rise/run.
MFM1P Overall Expectations
The math help provided for MFM1P Grade 9 Applied will address the following overall expectations:Linear Relations - LR3 - Demonstrate an understanding of constant rate of change and its connection to linear relations.
MFM1P Math Task Template
Check out this Math Task Template to get some practice in 5.10 – Graphing Linear Relations of the grade 9 applied math course.MFM1P Math Videos Related To This Topic
Check out these Math Videos to learn more about 5.10 – Graphing Linear Relations of the grade 9 applied math course.MFM1P Khan Academy Practice
Check out this Khan Academy Practice link to learn more about 5.10 – Graphing Linear Relations of the grade 9 applied math course.Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Access Other MFM1P Grade 9 Applied Resources
Not What You're Looking For?
Search MFM1P Grade 9 Applied Resources By Criteria:
Unit 0 - IntroductionUnit 1 - Measurement 2D and 3DUnit 2 - Measurement and OptimizationUnit 3 - Exploring Relationships - Lines and Curves of Best FitUnit 4 - Proportional ReasoningUnit 5 - Linear RelationsUnit 6 - Multiple Representations of Linear RelationshipsUnit 7 - Algebraic Models - Making ConnectionsUnit 8 - Geometric Relationships
Angle Relationships
Angles of Parallel Lines With Transversal
Area
Creating Equations
Data Management
Direct and Partial Variation
Distance-Time Graphs
Distributive Property
Exterior Angles of a Triangle
Extrapolation
First Differences
Geometric Relationships
Graphical Stories
Graphing Linear Relations
Graphing With Rise Over Run
Initial Value
Interior Angles of a Triangle
Interpolation
Interpreting Graphs
Interpreting Linear Equations
Investigations
Linear Equations
Linear Relations
Linear Relationships
Lines of Best Fit
Maximizing Area
Measurement
Minimizing Perimeter
Modelling With Equations
Non-Linear Relations
Optimization
Patterning
Percentages
Perimeter
Point of Intersection
Powers and Exponents
Predictions
Problem Solving
Proportional Reasoning
Pythagorean Theorem
Rate of Change
Ratios and Rates
Relationships
Representations of a Linear Relation
Representations of Linear Relationships
Rise Over Run
Scatter Plots
Simplifying Like Terms
Simplifying Polynomials
Slope of a Line
Solving Equations
Solving Linear Systems
Solving Proportions
Substitute Into Equations
Triangles
Unit Rates
Volume
Angles of Parallel Lines With Transversal
Area
Creating Equations
Data Management
Direct and Partial Variation
Distance-Time Graphs
Distributive Property
Exterior Angles of a Triangle
Extrapolation
First Differences
Geometric Relationships
Graphical Stories
Graphing Linear Relations
Graphing With Rise Over Run
Initial Value
Interior Angles of a Triangle
Interpolation
Interpreting Graphs
Interpreting Linear Equations
Investigations
Linear Equations
Linear Relations
Linear Relationships
Lines of Best Fit
Maximizing Area
Measurement
Minimizing Perimeter
Modelling With Equations
Non-Linear Relations
Optimization
Patterning
Percentages
Perimeter
Point of Intersection
Powers and Exponents
Predictions
Problem Solving
Proportional Reasoning
Pythagorean Theorem
Rate of Change
Ratios and Rates
Relationships
Representations of a Linear Relation
Representations of Linear Relationships
Rise Over Run
Scatter Plots
Simplifying Like Terms
Simplifying Polynomials
Slope of a Line
Solving Equations
Solving Linear Systems
Solving Proportions
Substitute Into Equations
Triangles
Unit Rates
Volume

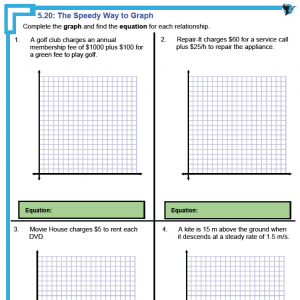
I was looking over the math template examples and have a question. Many of the real world examples would not be connected. A state test – at least once – stressed that you should not connect the dots if rational numbers are not part of the solution. Look at the yum yum ice cream shop example- you cannot buy part of a scoop. Should the graph be dot, dot, dot without connections? There is also limits to these problems – you cannot have a cone with “17” scoops -I would like one but it is unrealistic. Also you would only graph in Quadrant I. Many of the examples are like this. Thoughts?
Great thinking, Pete! I agree that the context drives what the graph would look like. However, this is something we discuss in class with students and not something that I am too rigid with since students could use rational values to be more precise and simply state that certain values are not realistic. Good points though!