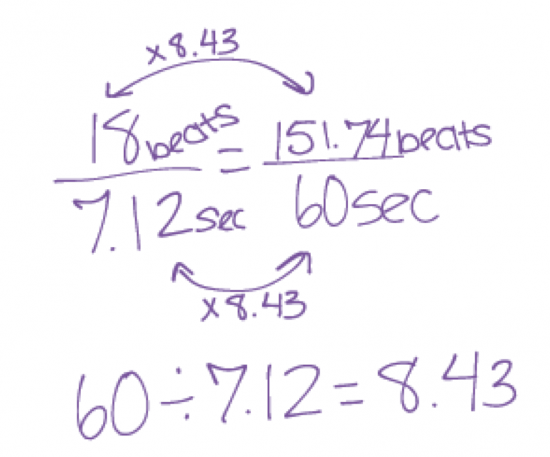How to Apply Proportional Reasoning Concepts to Other Strands
Through my work with the Middle Years Collaborative Inquiry Project with teams of intermediate math teachers from 29 different schools, it is clear that teaching in Ontario elementary classrooms can be tough. Teaching multiple subjects throughout the day, daily interruptions, and pressure to have adequate assessment data from each strand for report cards each term are just a few of the many pressures.
In some cases, teachers feel obliged to follow the textbook because they do not feel as confident in mathematics as they might in other areas of the curriculum. Since the textbook breaks curriculum into smaller “chunks,” it seems logical that this would be a easy and understandable way to teach mathematics. It seems as though textbooks are created with a focus on restricting math content to only the concepts introduced from that section or unit to avoid having to “re-teach” or “review” a previously learned topic from earlier in the course.
Lack of Retention and Ability to Apply Concepts
Unfortunately, this “chunking” of math concepts really restricts the possibility of making connections from one topic to another throughout the course of a term/semester or course. As math teachers, we have focused on students mastering procedures on a given day without any focus on how these skills apply to concepts learned previously or how they will apply to concepts we have yet to introduce. I think Dan Meyer sums it up very well when he said:
The maths serves the conversation, not the other way around.
If our math classes introduce interesting questions that require us to learn some math, we are more likely going to develop deeper conceptual understand and encourage retention of those concepts since they will have a memory (the question) to peg the concept to. Furthermore, if we are asking questions with context and avoid too much rote/procedural memorization, it is likely that concepts from previous (and future) math lessons will be required. It is really tough to provide “real world” questions while restricting the topic of the day to “Pythagorean Theorem.”
Making Connections in Proportional Reasoning via Baby Beats 3 Act Math Task
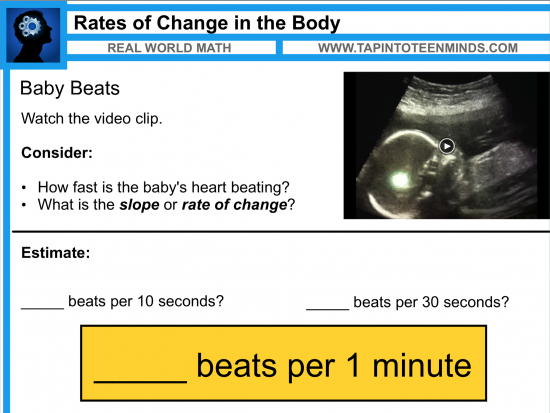
In the Baby Beats 3 Act Math Task I created recently, we have what seems to be a pretty simple question where students might ask: “What is a healthy heart rate for a baby in the womb?”
Not only can it help with their own understanding of how they can incorporate math into real-world scenarios, but it can also prepare them for when they’re ready to have children of their own. Pregnancy can be a scary time for both mother and father, but if they know that their child has a healthy heartbeat, all of these nerves can be put at bay. Of course, some people aren’t ready to have children at all so ask themselves the question – what is abortion? And is it the right thing for me to do? No one can make this decision but the people involved, so it’s important to lay out all your options before making a choice. Regardless of the route you go down, math can be applied to both situations, but we’re going to be looking at the healthy heart rate of a baby in this example.
As you’ll see in the video and from the screenshots below, this question can be extended well beyond a simple rate of change problem to involve many concepts from across the different math strands from 7 to 10.
Making Connections Across Math Strands
Because I have the opportunity to work with teachers from grade 7 to 10, I have used this same problem in all four grade levels in very different ways. Many math questions could be approached in a similar manner using different questions and extensions for each level. Let’s look at a few of the possibilities with any proportional reasoning question.
Proportional Reasoning: Rates and Equivalent Fractions
Regardless of the grade level, I like to start this problem off with some pure guesses. Regardless of the varying level of readiness from one student to the next, all students can toss out a guess based on “intuition” as Dan Meyer suggested in his TED Talk.
Here’s an example of where you might want to begin with this:
Whether intentional or not, this simple minds on for this problem actually introduces some basic equivalent fraction work as students must take their initial guess and determine the number of beats per 10 second, 30 seconds, and 1 minute.
Extending to Data Management: Tables and Graphs
After teaching for 8 years, I had introduced proportional reasoning concepts such as ratios, rates, and proportions on their own in a separate unit. Providing students with strategies such as solving proportions would be the ideal method to solve the problem. A solution for this problem would typically look like this:
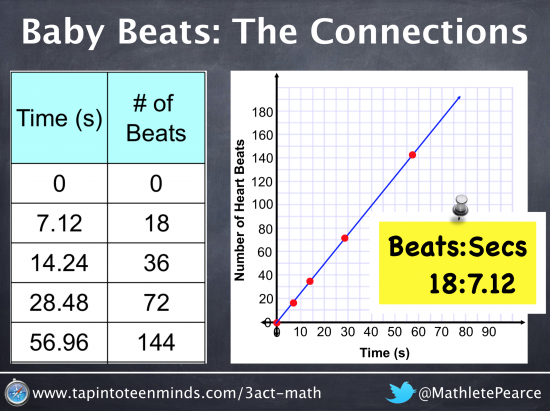
Over the past semester, I have been looking at how we can make connections from one strand to the next and while it is fairly obvious now, I cannot believe I would not introduce a table and graph as a strategy to solve such a problem. I always knew this was a possibility, but wonder if I was brainwashed by the “textbook approach” of how a proportional reasoning problem is supposed to be solved. It seems fairly reasonable for most of my students to be able to create a table of values (or ratio table) to get a visual of what is really happening here. Discussing independent and dependent variables as well as how to create a scatter plot are skills that could be introduced during the solution process of a question like this rather than taught as a prerequisite to solve a future problem.
Rates of Change and Unit Rates
Extending the equivalent fraction work that was carried out in the estimation portion at the beginning of the task, we can then take the change in y over the change in x to discuss how all differences in the table would yield an equivalent fraction. Students could then reduce the fraction to a unit rate that could be useful to help solve the problem more easily.
Connections Between Decimals, Fractions, and Percents
When I have discussions with grade 7 and 8 teachers about their Decimals, Fractions, and Percents unit, I can distinctly remember how boring it was as a student and how boring it is as a teacher. Rather than introducing them separately with no context, I see proportional reasoning problems like Baby Beats as an excellent opportunity to make this connection.
As you can see in the image below, there are some big connections to be made here. Rate of change could be represented as 18 beats per 7.12 seconds, or 18/7.12 in fraction form; followed by the unit rate of 2.52 beats per 1 second, or 2.52 in decimal form; and finally, 252 beats per 100 seconds, or 252% in percent form. The important piece here is that all three representations are really the same representation, but simply different equivalent fractions.
Linear Patterning With Initial Value and Rate of Change
What better way to begin the discussion around patterning than with a direct variation relationship, such as a proportion? The concept of initial value can be easily introduced since all proportions start at zero, leaving an equation with your dependent variable equivalent to your rate of change multiplied by the independent variable.
Why did I wait to introduce this concept until the “Direct and Partial Variation” section in the textbook?
Creating and Interpreting Linear Equations
Finally, we can then begin looking at the relationship between time and number of beats to create linear equations.
Proportional Reasoning Strategies Template
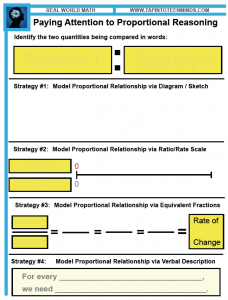
Feel free to download a handy template I created that could be beneficial for any proportional reasoning questions your students may be solving. Encouraging them to use different strategies can really help them solidify their understanding of the concepts.
Paying Attention to Proportional Reasoning
Access the Ontario Ministry of Education’s recent publication about Proportional Reasoning and the importance from K-12. Specific examples are included at each divisional level.
How are you making connections in proportional reasoning or other topics across different math strands? Share with us!
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog