Making Math Fun Through Curiosity, Collaboration and Failure
Yesterday was our first class after the Ontario weeklong March Break. I had plenty of time while travelling to reflect on what new approaches were working and what areas I needed to work on. Most recently, I have been trying to focus on making math tasks contextual, visual and concrete while also modelling the interconnectedness of topics throughout my course. My largest struggle is trying to break away from a very structured approach that really left no room for differentiating my lesson based on where the students were.
With the overarching learning goal focusing on the Distributive Property both with and without unknowns, I thought starting with a warm-up at the whiteboards was a good place to begin.
“Chunk” 9 x 12 Using an Area Model Without a Calculator
Students were first instructed to chunk 9 x 12 into “friendly” numbers to assist them in multiplying without the use of a calculator. Students had participated in some practice on the first day of the year with chunking their multiplication into friendly numbers in hopes that it would set them up nicely when we began introducing variables.
Something to note is that I wanted to start with really manageable numbers and with this group, many are not comfortable with their multiplication tables.
I then had students chunk 6 x 14 using the same method and all succeeded without much trouble.
In order to very slowly introduce the concept of a variable, we demonstrated what this could look like using the 6 x 14 problem:
Students then had their first problem to simplify with an unknown, 5(x + 6):
As students simplified this problem, I couldn’t help but think to myself that this had to be boring. While I tried to help students see that this type of problem called “distribution” is just like chunking our multiplication, I felt less than inspired having my students do problems for the sake of doing them.
While we haven’t really done too much with solving equations, I thought that maybe making this more of a challenge to find a missing number could be more intrinsically motivating. I then tossed this up on the board:
I was surprised by how dedicated to finding the missing number my students became. It is important to note here that I did not give them ANY instructions, steps, rules, or algorithms to solve an equation.
Students were able to very quickly simplify using a visual model from 9(x + 5) to 9x + 45, but then many were stuck. The only clarification I would give when students were stuck were variations of the following:
You know that 9 times a number plus 45 is equal to 99…
Can we determine what 9x is equal to?
Show me what part of your visual model represents 99…
After some thinking and collaboration amongst students in the class, we were able to look at quite a few different solutions that all focused more on logic and reasoning rather than an algorithm:
Extending to Multiplying a Monomial by a Monomial
We have done some work with Pythagorean Theorem using Dan Meyer’s Taco Cart as well as some visuals I’ve created along the way, so students are familiar with the geometric and visual representation of “squaring” a number. I was interested to see if anyone could make the connection to multiplying monomials:
This question stumped some students at first, but we had a quick discussion about what it means to multiply a number by itself and many were then off to the races. This question also allowed us to highlight some common misconceptions including the thought that 12x^2 is equal to 144x or 144x^2.
Students ASKED to be Challenged!
After this problem, I was thinking we’d move on to what I had planned. However, students were asking me to give them another to try and it became sort of a friendly competition. I was very surprised by this, but thrilled none the less. The next problem for them to solve was:
Consolidating Our Learning
My original intent was to use an animation to get my students thinking and engaged. As it turns out, it wasn’t really required. However, I did want to consolidate some of what we did today, so I thought I would introduce this question:
Students began working on the perimeter and I changed my approach to have them SOLVE for the unknown length of the pool noodle by giving them the total perimeter of 180 feet.
Overall, I was really impressed with how far we went in this lesson. I had no intention of attacking solving equations, but the opportunity presented itself and I’m glad that I went with it. Clearly, students (and I) got more value from this lesson by letting the learner lead their own learning. I’m hoping to build on this idea and share out the results.
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog



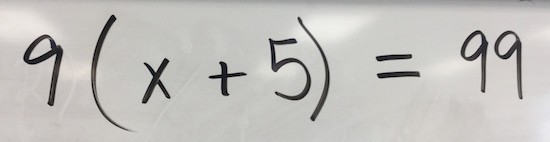
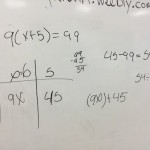




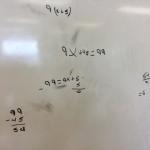

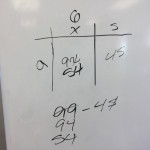


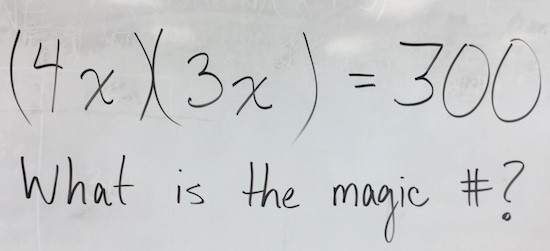
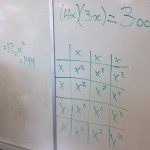


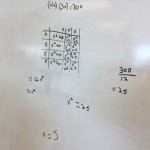


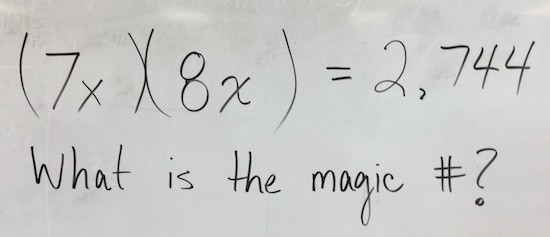
ASking to be challenge sounds like they trust you to make it an achievable one, which speaks volumes.
Lots of elementary teachers are really quick to move away from area model and transition to the algorithm because they never see where it goes. Really nice job Kyle of laying out the progression of the area model and the importance of sticking to it.
Although it’s goes beyond 3-5 content, I think it would be extremely beneficial to share this with elementary teachers anyways. It might help slow their roll and stress the importance of conceptual understanding.
I disagree Graham. As an elementary teacher I loathe the algorithm as it does not make much sense to the students whereas the area model makes sense. We spend a lot of time with it. The parents tend to dislike it though and try to move their students to the algorithm. Sometimes I question the value of the algorithm at all – I teach it (and it is HARD for the grade 4 & 5 students) because it is expected of me. When I teach it I try to ensure they understand it.
I think we do agree Erin…or at least I do with you.
I was suggesting that by showing elementary teachers (in a PL format) how the area model extends beyond elementary school, it could stress the importance in conceptual understanding…yet again.
The area model brings more to the table than just multiplication of whole number and teachers need to see how the model can be applied to decimals, factoring, and so much more. In doing so, I’d hope more teachers would move from the idea that the algorithm is a means to the end (when it’s definitely not).
Cheers to place value understanding!
Ah. I see what you mean now. I am only learning all this because I teach grade 8 also and because I read rhia blog. I did understand the value of the area model for place value and distributive property. We should ALL be given the opportunity to follow all the math concept through at least to grade 9!
I’m just starting this with my grade 8 class. I’ve been thinking about how to go about it and really struggling. I am learning myself as I go because I was taught with algorithms (and it did not serve me well once I arrived in grade 9). I’ve been using Cuisenaire Rods and reviewing balancing equations so far. We talked about the commutative property yesterday and were just getting to distributive property (using rods) when I had to dismiss the class. I’m going to use this to continue, I’ll do the distribution with the rods first and then I will move into algebra tiles as you have. I was wondering if you know of any 3/4 Act lessons that will make it more meaningful? I often search the spreadsheets with lessons but I have a hard time matching common core and Ontario curriculum (and I wish the lessons had explanations of the math for those of us who did not study math in uni). Also, I find that my “good” (I need another word here) students are engaged by playing with numbers but the others are not. I have 29 in my class and the discussions devolve because at least 1/3 aren’t listening. Sigh.
I did this yesterday and today and I have some who got it right away and claim the model is confusing but the numbers are not, some who like the model and some who still don’t quite get it. 29 Students. It’s hard. I get so excited thinking that this is it, it’s so good they will all get it. I need some differentiated tasks/problems to go with I guess. And real life situations too. 🙂 Thank you for this, it does help a lot and I shared it with a colleague today.