Sparking Curiosity With 3 Act Math Tasks

Looking to spice up your daily problem solving routine in your math class?

Serving up your math tasks in Dan Meyer’s 3 Acts of a Mathematical Story format are a great way to go!

When I was first introduced to 3 Act Math Tasks, it was when I heard Dan speak at an OAME Annual Conference. The idea of bringing the real world into my math classroom immediately resonated with me and I made a personal and professional commitment to start building these types of tasks into my lessons.

Although Dan and a huge number of others like Robert Kaplinsky, Graham Fletcher, Jon Orr, Dane Ehlert, and many others from the Math Twitter Blogosphere were openly sharing their tasks on the web, I found that the lessons didn’t always run so smoothly.

What I eventually realized is that while my immediate addiction to this type of task format was helpful for ensuring that I began the transformation that my lesson delivery desperately needed, I had failed to reflect on what elements were necessary to ensure my lessons ran without a hitch.

In this post, I plan to share a few key tips that I wish I was more intentional about when I began delivering 3 act math tasks in my own classroom.

SPARK CURIOSITY

What caught your eye about the 3 act math task you’ve found?

What made you think it would be useful for your classroom?

Often times, we can be tricked into thinking kids will enjoy a problem because it is from the real world, it is relevant, or because there is a video they can watch. These are all misconceptions. Think about how the problem might make a student curious to engage and solve the problem.

In the Gummy Worms 3 Act Math Task, I’ve made an attempt to Spark Curiosity.

Take a look.

But what makes this a curious moment?

CREATE ANTICIPATION BY WITHHOLDING INFORMATION

One of the best ways to make a curious moment is to avoid giving students all of the information necessary to solve the problem upfront. Withhold counts, measurements, and even the question you intend to ask as a means to address the learning goal you’ve selected for that lesson.

When first exploring 3 act math tasks, it is easy to miss the fact that the first video, act 1, typically gives little information about the question we are asking or any measured quantities. Much like a well written movie script, the filmmaker is intentionally giving just enough information to capture the attention of the audience and will build the storyline slowly to keep that attention.

In act 1 of the Gummy Worms task, you’ll notice that there really wasn’t a whole lot of anything going on. Just a jar placed on counter leaving students to wonder: “what the heck is going on here?”

In order for a 3 act math task to be successful, we must build anticipation in our students by withholding information that you typically get upfront in a textbook or on a worksheet. Dan Meyer talks about this more here.

NOTICE AND WONDER

Once we have built anticipation through the withholding of information, we can now empower student voice by asking them what they notice and what they wonder about the image or video clip.

Some common ideas shared during the notice and wonder portion of the Gummy Worms task include:

• There’s a jar with gummy worms in it.
• What does the tag say?
• Nice countertops!
• How many gummy worms are in the jar?
• Why is the jar so empty?
• How many gummy worms would it take to fill the jar?
• … and many others.

Be sure to leave this questioning open as asking for them to pay attention to only things related to mathematics may shut down some students, especially those who may not feel confident enough in their thinking. Some mistakes I’ve made in the first handful of years trying to use 3 act math tasks was asking questions like: “what is the question?” or “what math-related things do you notice and wonder?”

Questions like these sure did limit the conversation in my classroom to only include the more confident students and shut out those who aren’t so certain.

Once you’ve jotted down the noticings and wonderings of your students, it’s time to think about what questions you might consider solving. Of course you have planned out ahead of time which question you’d like to ensure that you answer to address a specific learning goal, however often times, students will have asked that question during the notice and wonder stage. If they don’t, that’s OK! It doesn’t always have to be the students who get to pick which questions we are going to solve and typically, the question I have in mind is a “gateway” question to give us enough information to answer other questions that have already been asked.

ESTIMATION

Did you know that the word “estimate” comes up in the Ontario curriculum 53 times while the word “calculate” only appears a total of 17 times?

Of course there are other words that imply “calculate” that we must consider, but my point is that estimation is an important part of building mathematics proficiency. Using the 3 act math structure to withhold information allows for a unique opportunity for students to engage in real, worthwhile estimations that we typically do not have when using traditional word problems from the textbook or a worksheet.

I can vividly remember myself as a student looking at questions like:

There are 7 rows of 6 cookies in the display case at the bakery.

a) Estimate how many cookies there are in total.
b) Calculate how many cookies there are in total.

After reading a question like this, I would routinely tackle part b) first to get an answer of 42 and then take 1 or 2 off to jot down my “estimate”.

This isn’t a great way to promote students wanting to take part estimation activities or develop their estimation skills.

With the 3 act math structure to approach problem solving, the anticipation we have built up through the withholding of information and engaging in the notice and wonder almost forces everyone to NEED to take part in making estimates.

This is where everyone puts some skin in the game and even a bit of friendly competition develops. Now everyone WANTS to know the answer to settle things.

A great strategy to get kids using their adaptive reasoning skills before just tossing out any old number for their estimate is to have students consider numbers that are “too low” and “too high”. This is a great way to help kids sort of “box in” a nice range for them to play in for their estimate. It might also get them thinking more deeply about the actual situation, slowly unravelling all of the details that might be in plain sight, but unnoticed until thinking about what is realistic.

Once students “box in” their reasonable estimate range, they can then go ahead and pick their “best guess”.

Allowing students to share their best guesses openly is a great way to set a range of estimates for the entire class. The beauty of this moment is that we can now look at the range of best guesses and come to a conclusion that we’ve got a pretty wide range of possibilities. This is where the mathematics begins to be a super helpful tool for us to narrow down that range to something much more precise.

At this point, you’re in a great spot to ask students for what other information they’d like to know in order to “improve” their estimates. Asking them to explain their reasoning for requesting that information can give you a nice window into their mind to determine what sort of mathematical thinking and strategies they might be ready to use.

Wanting to focus more on estimation specifically? Be sure to check out Andrew Stadel’s Estimation 180.

PROMOTE STUDENT THINKING

I’ll typically share out more information at this point or, like in the Gummy Worms 3 act math task, I reveal the answer to this first question as a means to get us to the intended learning goal for that day. In this particular problem, after students witness me take 25 gummy worms out of the jar, I then put a handful back in and they are left to determine how many I must have put in the jar?

Now, set them free on the task to solve it using any strategy they would like without pre-teaching them how they could/should or you would go about solving it.

This might be hard for some of us to swallow because we teachers always feel the need to ensure that kids can successfully attack the problem. Of course, we want to make sure we are giving tasks that they have an entry into, however we don’t want to be pre-teaching them or all of the curiosity, anticipation, and excitement is gone.

The most effective way to implement a 3 act math task or any other type of curious problem is to promote student thinking without explicitly pre-teaching the concept. If a lesson is taught before students have had an opportunity to solve a problem using their prior knowledge and through the inquiry process, this can immediately shut down some students who do not feel confident with the newly presented ideas and/or concepts.

Not only does pre-teaching rob students of the opportunity to think, but it can often lead teachers to feel as though 3 act math tasks “aren’t working” because students don’t appear any more engaged or interested in the math lesson than before. While it might feel like we are helping students by teaching the steps and procedures that will help them successfully solve the problem, we are often times helping only those who have strong memorization skills while leaving the others behind. Pre-teaching may result in the abandonment of this problem solving structure before experiencing the huge benefits.

FUEL SENSE MAKING

Plan with intentionality to fuel sense making as you help push student thinking in the direction of the new learning. Making use of the 5 Practices for Orchestrating Productive Discussions as you anticipate, monitor, select, sequence, and connect the mathematical ideas you have planned with intentionality will be extremely important to maximize student learning.

Selected specific students to share out their useful mathematical models and strategies prior to you sharing additional models and strategies you would like to highlight through direct instruction.

Although you can use individual 3 act math tasks for many different learning goals, one that I tend to use the Gummy Worms task for is to explicitly introduce and/or re-visit the part-part-whole or “parts whole” model for addition and subtraction:

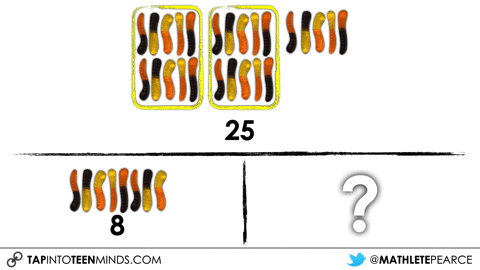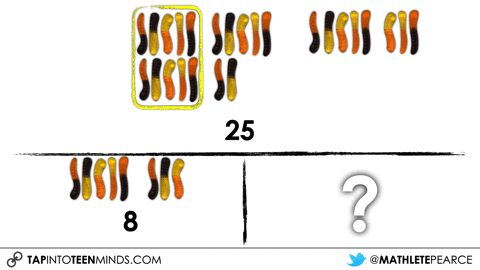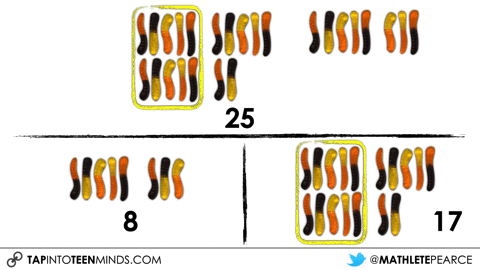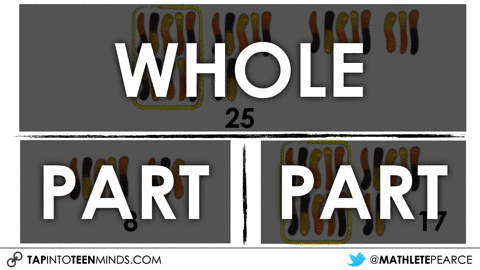
So while I’ve allowed different students to share out different strategies based on the 5 Practices, I am taking some time to do some explicit teaching through direct instruction to help push student thinking forward in the area of addition and subtraction structures. Here are some other addition and subtraction structures you might consider checking out on my site Math Is Visual.

THE BIG REVEAL

Just like a great Hollywood movie, Act 3 is the conclusion of the storyline.

In math class, this is where we share what really happened in the real world. It’s great to have a video or image for this portion, but not always a requirement.

Keep in mind that some 3 act math tasks might have act 3 come at the end of the task, or if you think about the Gummy Worm problem, the first act 3 came pretty early on after the estimating. However, once students are engaged and can visualize the contextual situation in their mind, you’ve got them for all kinds of mathematical learning opportunities.

PURPOSEFUL PRACTICE

Practice is something that isn’t discussed a whole lot during workshops, keynotes, and presentations which can often lead us teachers to make interpretations as to why that is. While many teachers tend to think that if you don’t hear about it any more, then it must not be a thing or “allowed”, I’ll argue that there are many great things that happen in a traditional math classroom that are still really useful today. You might not hear about them much, but I think that is because most people are aware that they exist and thus they aren’t really exciting to talk about during presentations and workshops.

Practice for your students in math class is important.

However, the way we go about practicing is really important.

Plan an opportunity for purposeful practice. Repetition when learning anything in life is really important, but focusing on too many reps too fast as well as focusing on speed can actually hurt more than help.

Think of ways that you can spread out your practice over time instead of all in one chunk. It’s also a huge bonus If you can make purposeful practice that is connected to the context/story from the 3 act math task, but this is not a requirement.

While I believe the ideas above would certainly help someone who is trying to implement 3 act math tasks in their classroom for the first time or to sharpen up on their current usage of this problem type, I’m pretty confident there are other important elements lurking in the background.

Can you help us identify some in the comments?

Also, if you’d like to take this learning on the run or share this with a colleague, be sure to download the printable 3 Act Math Tip Sheet here.