Over the past few years, I have been spending a lot of time thinking about proportional relationships. From unpacking the information in the Paying Attention to Proportional Reasoning document to meeting with a proportional reasoning symposium group through the Arizona Mathematics Project, my mind has been blown on a regular basis with how complex this seemingly basic and predictable mathematical concept actually is.
Having spent a ton of time teaching grade 9 courses in Ontario, the ideas we focus on all build on the learning of proportional relationships from previous years. However, because the content I was teaching was supposed to build on the ideas of proportional situations to move on to focus primarily on linear relationships, I found myself moving through the content quickly in order to get to direct and partial variation linear relationships graphically and algebraically.
I now realize that the vast majority of my students – including those I thought were “high achieving” – had an incomplete understanding of proportional relationships.
How do I know?
Because I had an incomplete understanding of proportional relationships myself.
There is so much goodness to unpack in the area of proportional relationships and I’m still finding myself going down rabbit holes with colleagues like Jon Orr, James Tanton, Dick Stanley, and Yvette Lehman to better understand how it all fits together.
To give you a bit of a backstory, most schools in my district have had student and teacher learning needs identified in fractions, measurement, and proportional reasoning, so the math team (Yvette Lehman, Andrea Lewis-Longmuir, Shelley Pike, Angeline Humber, and I) has been actively trying to create meaningful math professional development to highlight the very important connections between all three areas.
The task that we wanted teachers to engage in and then lead in their classrooms with students in Kindergarten through Grade 8 (modifying where appropriate) was a simple problem transformed to be more curious and problem-based centered around this question:
At a party, guests ate 14 packages of Reese’s Peanut Butter Cups.
There is 1 sixth cups of sugar in each package.
How much sugar is in 14 packages?
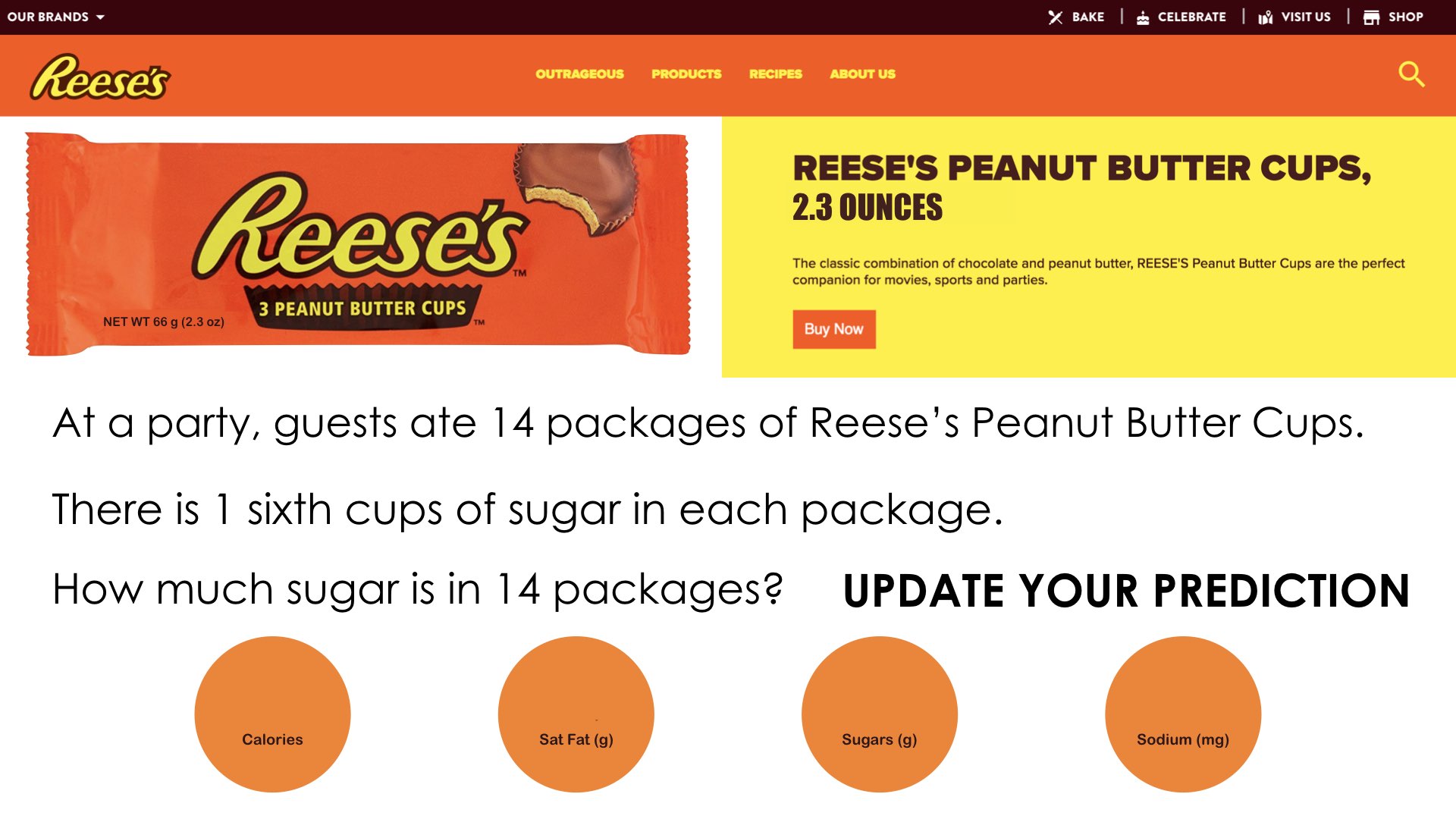
This proportional relationship word problem was made much more curious by avoiding the rush to share the specific details of the problem by starting with something a little more open and low floor.
Dig into this transformed low-floor, high-ceiling proportional relationships lesson.
For this particular math task, we first withheld the information of how much sugar is in each package to have students make a prediction of how much sugar would be in 14 packs. That lowers the floor and also gives you some perspective about how much your students know about the sugar content in food, whether they have an understanding of units of measure for mass and much more.
When we engaged in this task as teachers, we anticipated certain student solutions, but most (including myself) were quite surprised at how few solution strategies students had when they did the task. Regardless of the grade level and how the task was modified to be more accessible for younger learners, there was a lot of procedures and not a whole lot of mathematical models demonstrated through the use of tools and representations.
Before moving on, I’d recommend that you stop and do the following:
- solve this task in as many ways as you can using various concrete, visual, and symbolic representations;
- consider what students must be able to do before they are able to be successful with this task; and,
- think about how this task can be modified to ensure that all learners in your classroom have an entry point to this task.
Once you’re done doing that, come back and then have a look at some of the modifications that were made for a couple different grade levels as well as how students approached this task.
Modifications For A Grade 1 Classroom
After discussing possible modifications we could make to the task to help students in a grade 1 class access the task with the math learning team at an elementary school, we went to give it a try.
Here’s the modifications we landed on:
- Change the quantity of packages from 14 to 5 packages of Reese’s Pieces.
- Change the quantity of sugar and units of measure from 1 sixth cups of sugar per package to 1 half cups of sugar per package.
We also ensured that we had tangible materials for students to use. In this case, both real sugar and a non-standard “cup” that was transparent so the students could clearly see approximately half of each container without having to worry about the complexity and abstractness of standard “cups”. The best we could find in this case was 5 glass beakers with no standard units of measurement marked on the sides. We also had 5 printed images of Reese’s Peanut Butter Cup packages.

When we introduced this task to most educators, many believed that there would be no way for any younger students from say Kindergarten to Grade 2 to access this task. However, with slight modifications, we can get students thinking fractionally and start them on their proportional reasoning journey. These students were able to count how many half cups (or half beakers) of sugar there would be for 5 packages of Reese’s Peanut Butter Cups!
Some questions we could ask to stretch their thinking include:
- How many half cups of sugar would we need for 6 packages of Reese’s Peanut Butter Cups?
- How many half cups do you need to make a whole cup of sugar? (remove the other 3 packages and cups to focus their attention on just 2 cups)
- Give the students a whole cup of sugar and ask them to pour it into as many half cups as they can. What happened? How many half cups are there?
- What would happen if you pour 2 whole cups of sugar into as many half cups as you can?
In this particular case, these students were able to count how many halves, but were currently stuck at regrouping to determine how many whole cups there would be. This is something we can work with these two on by providing more experiences and by considering using different tangible materials (i.e.: whole apples and half apples, etc.).
Modifications For A Grade 4 Classroom
After seeing how much amazing thinking our friends in Grade 1 could do with this task, what do you think this task could look like in a Grade 4 classroom?
If the students in the class are comfortable with the fractional language of halves and fourths (not just quarters), it is realistic to think that students could work with this problem using the same situation of 1 sixth cups of sugar. However, working with 1 fourth cups of sugar could work to lower the floor.
With this group, we attempted the task “as is” to see what students could do and learn more about where we should go next.
The tangible materials and concrete manipulatives we had available were:
- Printed images of Reese’s Peanut Butter Cup packages;
- Connecting cubes;
- Relational rods;
- Square tiles;
I’ll recommend again that you stop to anticipate what student thinking might come out of this if you haven’t already. Maybe your thinking has changed since you saw the grade 1 students work on this problem.
Now that you’re back, let’s have a look at our first group of students who used the printed packs of Reese’s and single connecting cubes to represent 1 sixth cups of sugar and then simply counted how many sixths they had in total.


Here’s these students sharing their thinking:

Many of the groups required teacher prompting and that suggested to me that modifying the task to a lower number of packages and maybe 1 fourth cups of sugar with tangible materials might have been useful for this group before getting to this point.
However, once students were able to represent the 14 sixth cups of sugar, many were able to regroup to unitize. Many teachers in later grades are frustrated when students cannot convert from improper fractions to mixed fractions and that is exactly what these students were doing with relative ease.
Some questions / next steps to stretch their thinking include:
- Engaging in paper folding activities where students are taking whole pieces of paper and partitioning by making folds, cutting up the pieces and re-grouping;
- Using other foods that are typically partitioned from wholes into parts like apples, cucumbers, cakes, brownies, etc.;
- Asking students questions that promote fractional thinking through counting unit fractions to build fluency and flexibility;
Modifications For A Grade 7 Classroom
The next classroom we went into was a grade 7 classroom.
Based on what we’ve witnessed in grade 1 and grade 4, what sorts of modifications and/or materials would you have ready for these students?
Take a moment to reflect.
Maybe jot down your thinking on a scrap piece of paper and then come back.
Alright, now to give you the full story on this class, the teacher had left this task as a diagnostic while she was away at professional learning the previous week. She let us know that they had not done any work explicitly on fractions or proportional relationships, so this was definitely just to get a baseline of where students are and what they are bringing with them from previous years.
What we had found was that for the students who solved the problem correctly, most had relied on procedure and converting to a decimal to come to their solutions. Only two (2) others had relied on a concrete or visual representation to show their thinking. Many other students were trying to rely on a procedure symbolically, but when they applied their strategy incorrectly, they were unable to determine whether their answer made sense. This is very common in the intermediate/middle school classrooms I work with.
We decided to go back in and ask students to help us understand their thinking and give us an opportunity to press for understanding a wee bit.
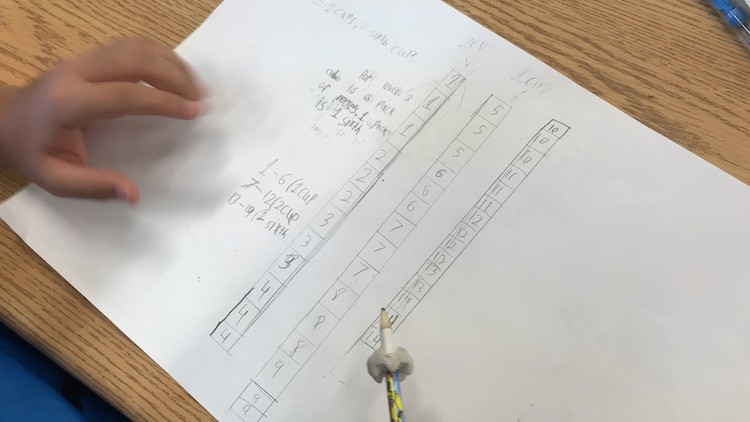
This first student had a visual set / bar model and it was clear on his paper that he had been able to count and regroup / unitize to whole cups of sugar, so I wanted to ask him to take me through his thinking. I wasn’t quite sure why he had listed the numbers 1 through 14 each 3 times.
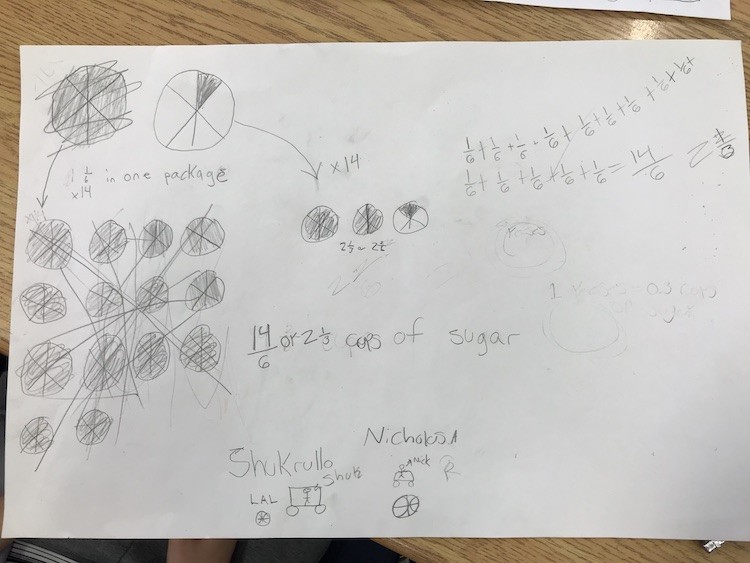
With the following group, I asked them to show their thinking as they only had represented their solution symbolically as 14 x 0.6 = 8.4
Here’s what they did:

Another group had successfully found the total amount of sugar in 14 packages by converting to a decimal and multiplying by 14 symbolically.

Another group had initially believed that 1 sixth cups of sugar was the same as 1.6 cups of sugar.
After encouraging them to represent their thinking, they were able to verbally describe the quantity of sugar as 14 sixth cups of sugar and regrouped / unitized successfully.
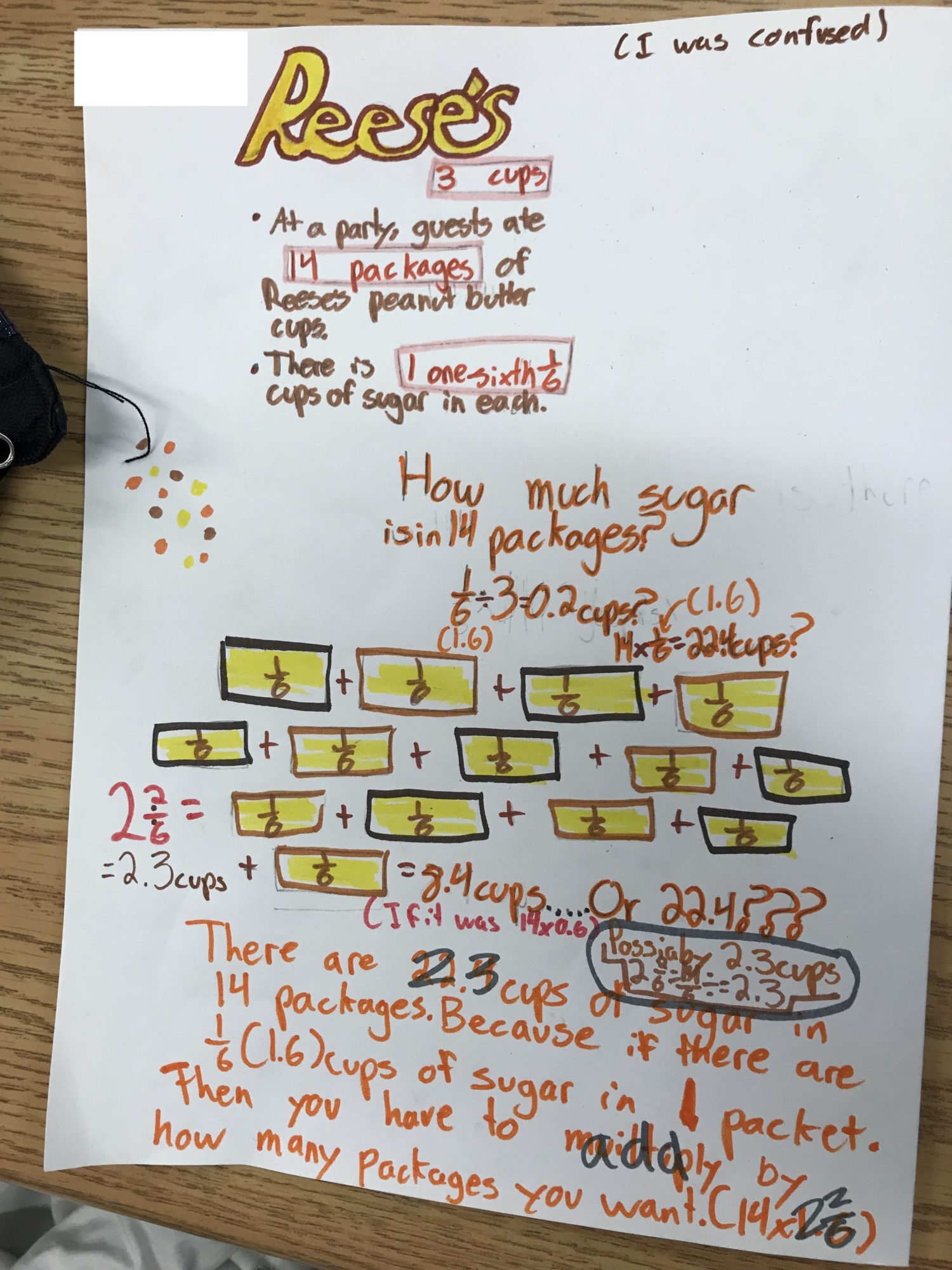
- Asking students to show what 0.6 looks like using a linear, area, set and volume model (modelling will likely be required);
- Asking questions similar to this that make use of linear, area, set and volume models to encourage students making use of those tools and representations;
- Explicitly using fractional language that encourages the counting of unit fractions to build fluency and flexibility;

What Is Your Biggest Take Away? What Questions Do You Still Have?
What was your biggest take away from this post?
What questions do you still have?
In order to truly learn, you must generate new knowledge and understanding through reflection. Without it, new ideas will wash away like footprints in the sand. I can’t wait to read your thoughts in the comments.
If you found this post helpful, we certainly aren’t done with proportional relationships yet! We are actually just getting started!
There is a complete Roadmap to Proportional Relationships that we unpack in our online proportional relationships course called The Concept Holding Your Students Back. Check out the first module introducing Proportional Relationships and why this work matters. If you enjoy it, you should join us along the entire journey over 9 modules from counting to algebra!
