Tapping It Up a Notch: Pythagorean Theorem – Part 2
In our last post, we used an inquiry/discovery approach to help students visualize how we can find the hypotenuse of a right-angle triangle when given the lengths of the two legs.
In this post, we will now introduce the General Case for Pythagorean Theorem in an attempt to use the same visual model to derive the formula for Pythagorean Theorem.
Using Pythagorean Theorem to Find the Length of the Hypotenuse
Visual Representation of Any Right Triangle [General Case]
In this video, we now introduce the concept for any right-angle triangle. Using the video from the previous post is probably a good idea as a starting point.
Summary of Pythagorean Theorem Video
Starting With The General Case Visually
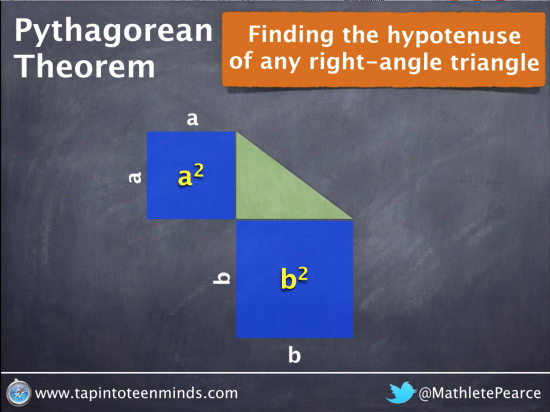
We now start with variables representing any side lengths for a right-angle triangle.
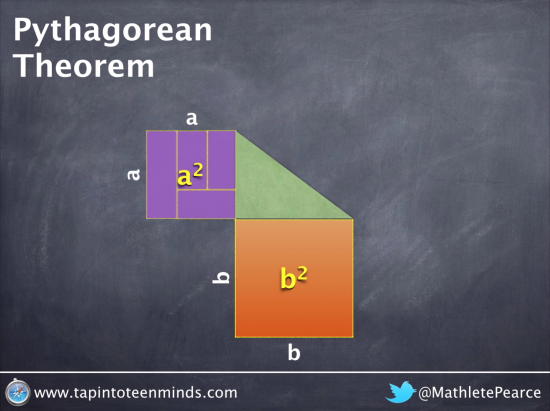
Connect Squaring Side-Lengths to Area
Once again, we show that squaring side lengths on the right-angle triangle will yield an area since we are multiplying length by width (or side by side, in this case):
Segment the Area of the Shortest Leg into Pieces
In order to preserve the visualization of the sum of the squares of both legs being equivalent to the square of the length of the hypotenuse, we will need to chop up one of the areas into pieces:
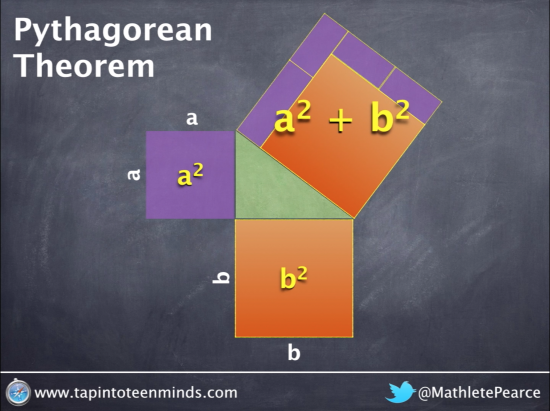
Show The Sum of the Squares of the Leg Lengths Algebraically
As we did in the 3, 4, 5 case in the previous post, we now must use algebra to show what the sum of the squares of the leg lengths look like. This can help students start to see what the formula must be.
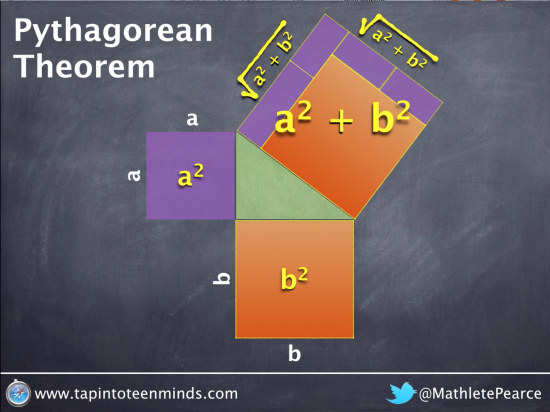
Finding the Length of the Hypotenuse
In the previous case, finding the side length was pretty easy for students to do without necessarily consciously thinking about opposite operations. In this case, we must square-root the resulting area to find the length of the hypotenuse.
Introduce c^2 as a Variable to Replace a^2 + b^2
Using substitution, we will replace a^2 + b^2 with a new variable, c^2.
After students are comfortable with the algebra behind Pythagorean Theorem, you may choose to discuss this more deeply. Having students understand that we are actually substituting c with the square-root of a^2 + b^2 could be beneficial as they get closer to advanced functions and calculus.
Deriving the Formula for Pythagorean Theorem
Students may now be more comfortable understanding and using the algebraic representation of the Pythagorean Theorem Formula:
Another post is forthcoming to help students better connect the visual representation of Pythagorean Theorem and the algebraic representation.
What do you think? How can we improve the introduction of this very important mathematical concept? Leave a comment below!
Other Related Pythagorean Theorem Posts:
[postshortcode the_query=”post_type=post&p=14140″]
[postshortcode the_query=”post_type=post&p=14185″]
[threeactshortcode the_query=”post_type=realworldmath&p=3760″]
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog



I like your general proof. You might be interested in this Sketchpad file I made to generalize this for the area of any regular shape used (instead of squares).
http://mail.wecdsb.on.ca/~david_petro/sketches/PythagoreanAreaV5.gsp
Thanks!
Very interested to check out the file. I am on my MacBook Pro and don’t have Geometer’s Sketchpad installed (probably should). Will check out on my iPad! Sounds like a pretty cool idea if I understand you correctly. Hope summer is treating you well!
Got a moment to check out your Sketchpad file and it is really cool! I think it is worth exploring in class to show students that the shape you choose is irrelevant, but a square is most efficient.