Tapping It Up a Notch: Pythagorean Theorem – Part 1
Over the past school year, I have been making attempts to create resources that allow students to better visualize math, build spatial reasoning skills and make connections to the algebraic representation. While some hardcore mathletes might balk at much of these attempts as not being real mathematical proofs, my intention is to help students (especially struggling students) visualize and make sense of why we do what we do. Too often, when a student asks us “why” a formula works, we are quick to show an algebraic proof that likely means very little to the student. If a student does not have the required algebraic understanding mathematically, one (or both) of these two possibilities may result:
- The student may get more confused and frustrated, or
- The student may never ask a question like that again.
I am definitely not trying to suggest that algebraic proofs are not important, because they definitely are. They are important when students are comfortable enough with the algebraic language of math. Until then, the proof serves little purpose.
For Pythagorean Theorem, showing some visual representations and making connections to the algebra are great places to start in middle school and intermediate divisions.
Using Pythagorean Theorem to Find the Length of the Hypotenuse
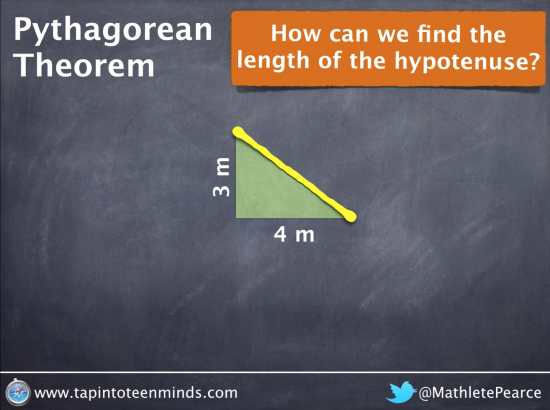
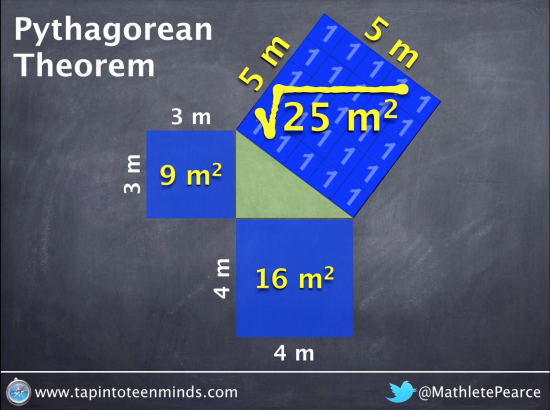
Visual Representation of a 3, 4, 5 Right Triangle
In the following video, I believe starting with a simple example and making the visual connection early is important. You’ll notice that the Pythagorean Theorem is being used, but without any formal algebraic representation. Check out the video below and the screenshots that follow for a quick visual:
Summary of Pythagorean Theorem Video
Starting With a Simple Example Visually
Selecting a right-angle triangle with friendly numbers that yield perfect squares such as 3, 4 and 5 is a great place to start. Ensuring students have an understanding of what the hypotenuse is and how you can quickly identify it is important prior knowledge.
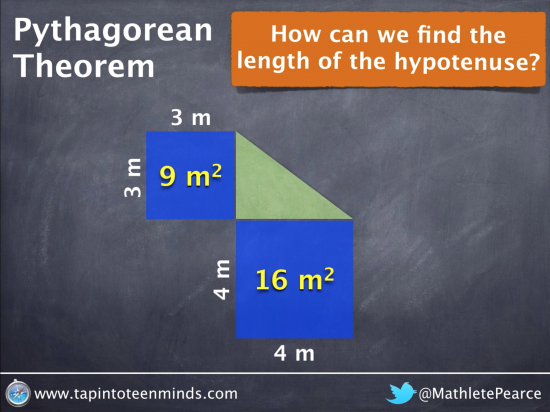
Making a Visual Connection to Squaring a Number
Many students have a really difficult time understanding that squaring a number can be represented as multiplying two numbers in an array. I often suggest that squaring a number gives an area since we are multiplying two numbers and thus yields 2 dimensions.
Here, squaring 3 and 4, we get an area of 9 and 16 respectively:
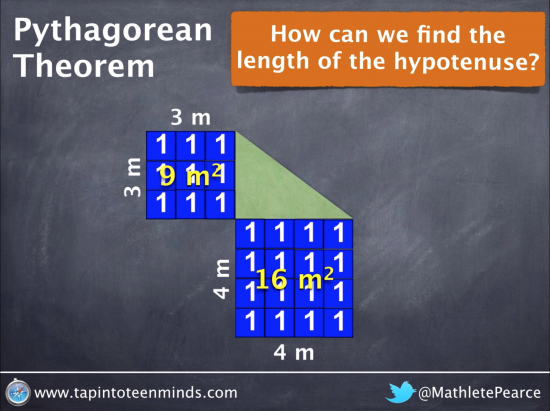
Visually Proving Sum of the Squares of Two Shorter Legs Equals Square of Hypotenuse
I want to make sure my students don’t just “do stuff” in math because the teacher said so. I want them to get some of the background behind how a formula was created and give some perspective of how much work had to be done to actually realize that a pattern exists. This example doesn’t give us confidence this will always work, but it surely gives students something to peg their understanding to when they need to utilize Pythagorean Theorem in the future.
Here, we use unit algebra tiles to show the area of the squares of both legs:
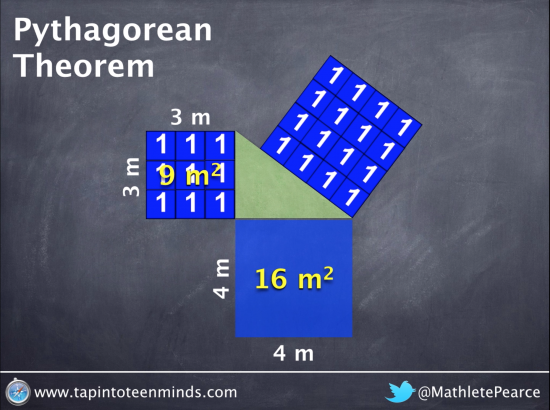
Watching the Squares of the Legs Add to Square of Hypotenuse
In the video, students can watch the unit tiles move from the squares of the legs to the square of the hypotenuse to see that they do completely fill the square of the hypotenuse:
Now, we can start discussing to see if we can make a generalization here.
Finding the Length of the Hypotenuse
Sometimes you may have to redirect students to what the original question was. Did we want to find out the square of the hypotenuse or the length of the hypotenuse? Without much effort, students can typically tell you the length without necessarily thinking about the opposite operation involved. This is fine at this point, but making a connection to what they actually did in their head to find it will be important moving forward:
The Final Answer
You’ll notice in this video and from the screenshots that we haven’t even introduced the actual formula yet. I hope you find this video useful as you look to try and develop the formula together with your students and then begin advancing to an all algebraic approach once students are comfortable and confident with the concept.
Check out the next post in this series as you scaffold students forward with Pythagorean Theorem shortly…
What do you think? How can we improve the introduction of this very important mathematical concept? Leave a comment below!
Other Related Pythagorean Theorem Posts:
[postshortcode the_query=”post_type=post&p=14156″]
[postshortcode the_query=”post_type=post&p=14185″]
[postshortcode the_query=”post_type=post&p=14649″]
[threeactshortcode the_query=”post_type=realworldmath&p=3760″]
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog