Spiralling Through the Curriculum With (too much?) Structure
Yesterday, I shared a task template I created for Dan Meyer’s Super Bear 3 Act Math Task colleagues from the Math Twitter Blogosphere (#MTBoS):
Super Bear 3 Act Math Task Template is now up. Feedback? —> http://t.co/QAboGiKKDn #MTBoS @ddmeyer @mathycathy @mr_stadel @robertkaplinsky
— Kyle Pearce (@MathletePearce) March 6, 2015
Some of my best learning and growth happens when I toss my ideas out there and ask for feedback from a wealth of math instructional knowledge from around the globe. Some feedback was positive:
@MathletePearce Love template structure & emphasis on multiple representations to help Ss extend task! @ddmeyer @mr_stadel @robertkaplinsky
— Cathy Yenca (@mathycathy) March 6, 2015
However, while I think “WE” as teachers feel more comfortable with a structured lesson and a game-plan through some sort of black line master or worksheet, it is possible that too much structure could hinder the process of critical thinking and choice for our students. I’m glad that my PLN will also challenge me to think differently:
@MathletePearce @mathycathy @ddmeyer @mr_stadel I like the mult. reps. Be careful that the scaffolding doesn't prohibit Ss critical thinking
— Robert Kaplinsky (@robertkaplinsky) March 6, 2015
@MathletePearce @ddmeyer @mathycathy @robertkaplinsky I’m curious to know more how you’d roll this out.
— Andrew Stadel (@mr_stadel) March 6, 2015
@MathletePearce @ddmeyer @mathycathy @robertkaplinsky I’d feel overwhelmed as a student seeing all this math structure in front of me.
— Andrew Stadel (@mr_stadel) March 6, 2015
The purpose of the template (often times) is to not only provide some sort of opportunity to consolidate and help students organize different strategies, but also to ensure that I don’t forget to make some of the connections. I am a huge advocate for developing understanding in an organic fashion through inquiry/discovery, but find that it can be difficult to pull it all together at the end.
What We Did…
While I promote the logic of a 4-part math lesson and typically begin with a “Minds on” or similar activity to activate prior knowledge, with this task, we dove straight into the Super Bear task. I showed students Dan Meyer’s intro video:
We spent some time developing questions and narrowing down to one before I asked students to head to the whiteboards. Students then made predictions about how many mini-bears would it take to make a “super bear” and then we showed the act 2 video giving the weight of 10 mini-bears:
Students then used their prior knowledge and intuition to find strategies that helped them determine how many mini-bears it would take. Here are some samples:
Surprisingly, most students selected a very similar approach involving division and multiplication (no diagrams, visuals, tables, graphs, etc.). All students, except for one, divided the weight of the super bear by the weight of 10 mini-bears. Some got stuck on the meaning of the result. With some student discussion and some questioning from me, each student was able to determine that what they had was how many “groups” of 10 mini-bears they needed for a super bear. The lone ranger who went down a different path found the unit rate, then divided the weight of the super bear by the unit rate to determine how many mini-bears it would take.
We had them solve for how many regular bears it would take as well. All students chose the same strategy for this part, even after I encouraged them to attempt finding another way.
At this point, we looked at the math task template and essentially skipped the first portion. Maybe I should exclude this section from the template for future use? I just worry that teachers who want to get started with 3 act math may want something more structured in order to get started.
However, I did have students take photos of their work from the whiteboard and put it in the Given Information & Workspace section:
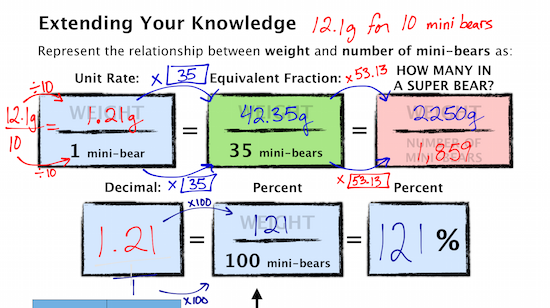
We did have a good discussion about ratios and rates. We have discussed the difference earlier in the year, but we haven’t really done anything formal with the terms. Hoping to keep bringing it back throughout the year as we make connections from proportions to direct variation linear relations. Students voted on which they thought made sense and then we had them defend their decisions. Some changed their votes as they articulated the “why” for their vote, which is great:
We then consolidated our learning and made connections between how students solved the task and some other strategies. Since I am trying to avoid having formal “sit-n-get” lessons on proportions, unit rate, percentages, etc. I am trying to make these connections based on student prior knowledge. Here’s what the group came up with for equivalent fractions, proportional reasoning, unit rate, and percentages:
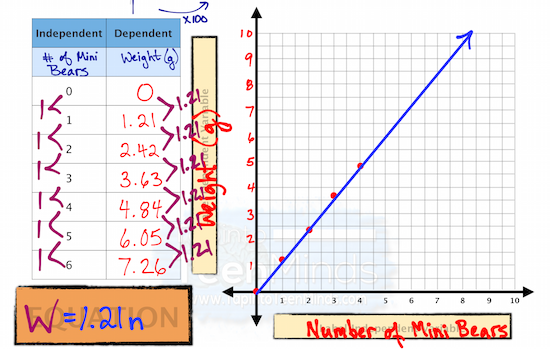
We then went on to look at connections in a table and graph, followed by looking at the first differences which students have been using to create an equation:
What folks like Jon Orr and I are trying to do is get away from lessons that silo content into sections and chapters. Typically, this “unit” format of teaching hinders these connections and promotes teachers introducing concepts prior to introducing problems that necessitate the concept.
In order to do this spiralling or interleaving of learning math concepts, it takes a lot of organization on the teachers part and many opportunities to introduce more than one concept at the same time. I know that this approach is a lot for students to handle upfront; however, that is why I am scaffolding so much at the beginning. I want students to learn topics and make connections at the onset rather than waiting until exam time to try and tie it all together. My hope is that these templates offer some of the organization and structure that will be lacking now that I’ve axed units and the approach of mass practice.
This is all brand new to me, so I’m hoping to continue leaning on my PLN and the #MTBoS to help me and my students grow through the process. I would appreciate any feedback you could provide in the comments section.
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog




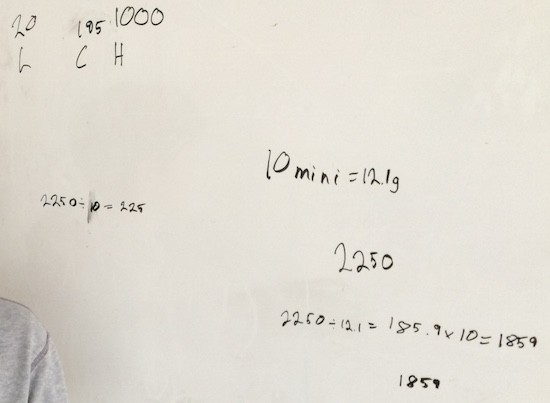
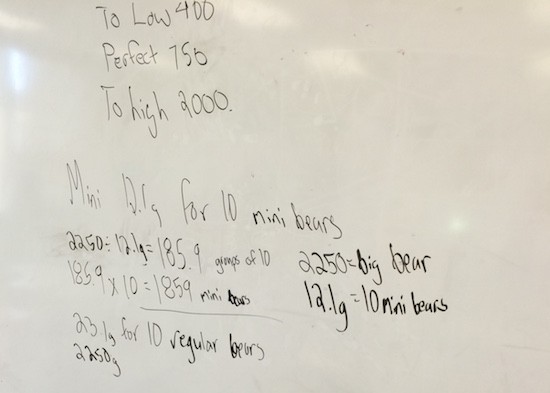
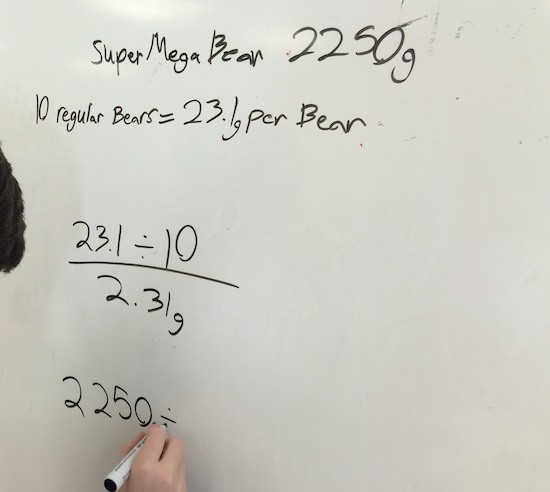



I tend to agree. I’m a fan of whiteboarding and let them struggle before they see any formal template from me. If I hand something out in advance I feel like it ruins the surprise or influences their thinking. Great reflection and sharing here. Thanks Kyle.
Thanks for the feedback, Jon. I appreciate our conversation last night regarding how I was going to implement this. This is the first semester I’ve been using my whiteboards for almost every lesson. Loving it! Students technically have whiteboards on their iPad – but being up and having a view of the work of their peers is a great opportunity I’ve been missing out on.
I think the key is keeping any sort of structured template for the making connections / consolidation process AFTER students have solved the problem using ANY strategy. This is where we can then try to introduce the learning goal / strategy I had intended to address that lesson.
I have to say that this new approach is really fun to teach and the students seem pretty immersed in the math. Fun times.