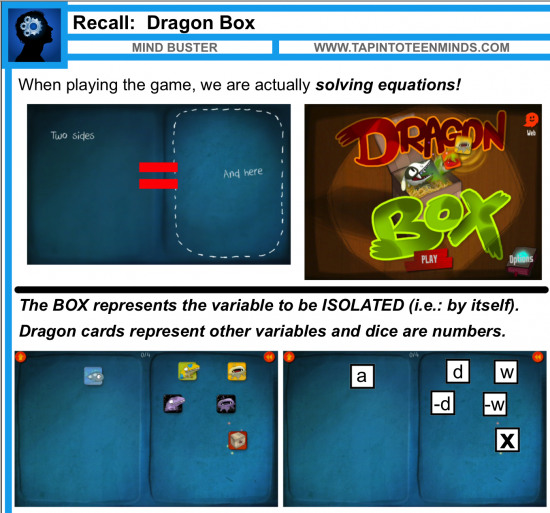
Those who follow my blog would know that I am a big fan of DragonBox to support learning how to solve equations. The gamification of solving equations has allowed me to give students at different levels of readiness an easy entry point to the learning behind a topic that is typically considered difficult by most.
Quick Summary of Dragonbox
Like most modern games, rules are very simple to start with more complex rules slowly introduced when necessary. The only information given to start the game are that there are:
- two sides,
- some cards, and
- to win… you must isolate the box on one side.
As you play the game, little hints are given to slowly reveal rules of the game. For example, in the first level, the player is instructed to “tap” any green circular tornado cards. Once you do, they disappear. Very slowly the game scaffolds rules into place including “day” and “night” cards for positive and negative terms, opposite operations, and more.
How to Effectively Use DragonBox in Your Solving Equations Lesson
In the past, I would allow students to play DragonBox for the first 10-minutes of our 75-minute class for about a week leading up to my solving equations lesson. While this gave students some context to work with when introducing how to solve equations, I felt that this game was too good to simply make connections verbally. I wanted something visual for students to work with as we slowly introduce solving one- and two-step equations.
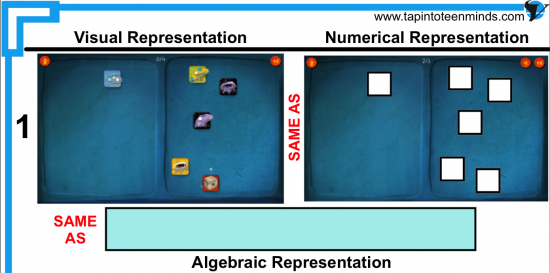
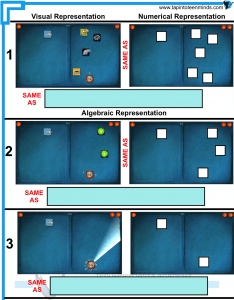
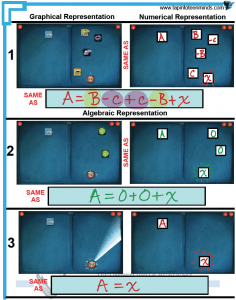
This time around, I took screenshots of different levels in DragonBox and each step required to isolate the box. The goal is for students to take the visual representation of the equation and assign variables/constants to each card and then represent these variables/constants as an algebraic equation.
Reflections After Day One of Solving Equations
This time around, students had not played DragonBox prior to the lesson. I gave them 10 minutes to experiment with the game and then we had a full-group discussion about the rules of the game and how they related to math. We then used the resources (that I’ve included at the bottom of the post) to make algebraic representations of different DragonBox levels and shared out over Apple TV.
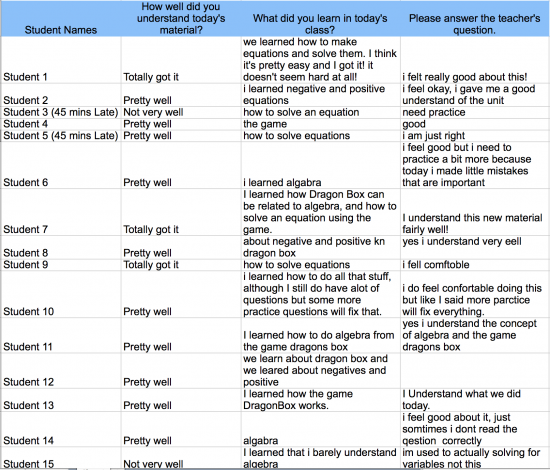
We slowly took away the DragonBox levels as a starting point and went straight to solving two-step equations beginning with the algebraic representation with success. My suggestion for next time might be one-step before two-step (unsure why I jumped over one-step? Odd!). However, I left that class feeling like students have a pretty solid understanding and the Socrative Exit Ticket responses correspond to my feelings:
The exit ticket quickly told me that:
- Three (3) students “totally got it”
- Ten (10) students understood “pretty well”
- Two (2) students understood it “not very well”
Comments like:
I feel good but I need to practice a bit more because today i made little mistakes that are important.
and
I feel good about it, just sometimes I don’t read the question correctly.
tell me that we are on the right track.
I will be compiling some new DragonBox levels as a Minds On to start the class, then we will address solving equations that we had encountered in the previous unit to ensure students can still see the connection between the initial value and rate of change of a linear relationship.
Resources:
Feel free to use the following material in PDF form to scaffold the introduction of solving equations with the use of the DragonBox app. I would also consider using the Algebra Touch app as a means for students to better understand how to solve equations when represented algebraically.
Supporting Resources |
What It Might Look Like |
Download Dragonbox on iOS from the App Store
Dragonbox for Ages 5+
|
Dragonbox for Ages 12+
|
Hope you find this beneficial in your classroom! If you’ve done any additions to make this even better, please do reach out in the comment section so we can add a link!
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog


Trackbacks/Pingbacks