Turning a Less Than Effective Lesson Into a Growth Opportunity
Today, we extended our learning goal from the previous day from:
I can find the point of intersection of two linear relations on a graph and interpret the meaning of the intersection point related to a real world situation.
to the following learning goal:
I can solve multi-step linear equations using a variety of tools and strategies. (i.e.: 2x + 7 = 6x – 1)
For years, I would simply extend our work solving linear equations in Slope/Y-Intercept (y = mx + b) Form by adding additional terms on both sides of the equation. However, I found that we were quickly moving from a deep conceptual understanding of rate of change and initial value to no meaning at all. Although solving systems of equations algebraically is not introduced in the Ontario applied math curriculum until grade 10, I decided it was worth the extension:
I can find the point of intersection of two linear relations using the algebraic method of substitution.
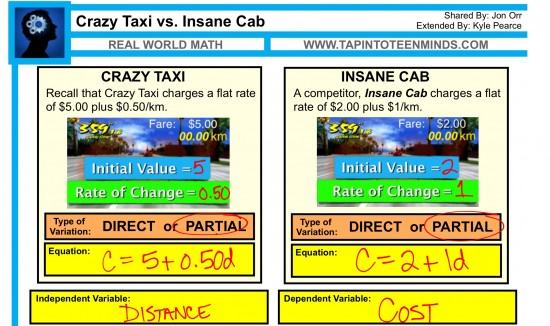
Today, we extended the concept of Jon Orr’s 3 Act Math Task Crazy Taxi by adding a second option, Insane Cab:
Crazy Taxi: C = 0.50d + 5
Insane Cab: C = 1d + 2
We started with the bar really low, offering an opportunity for students to use their prior knowledge of linear relations:
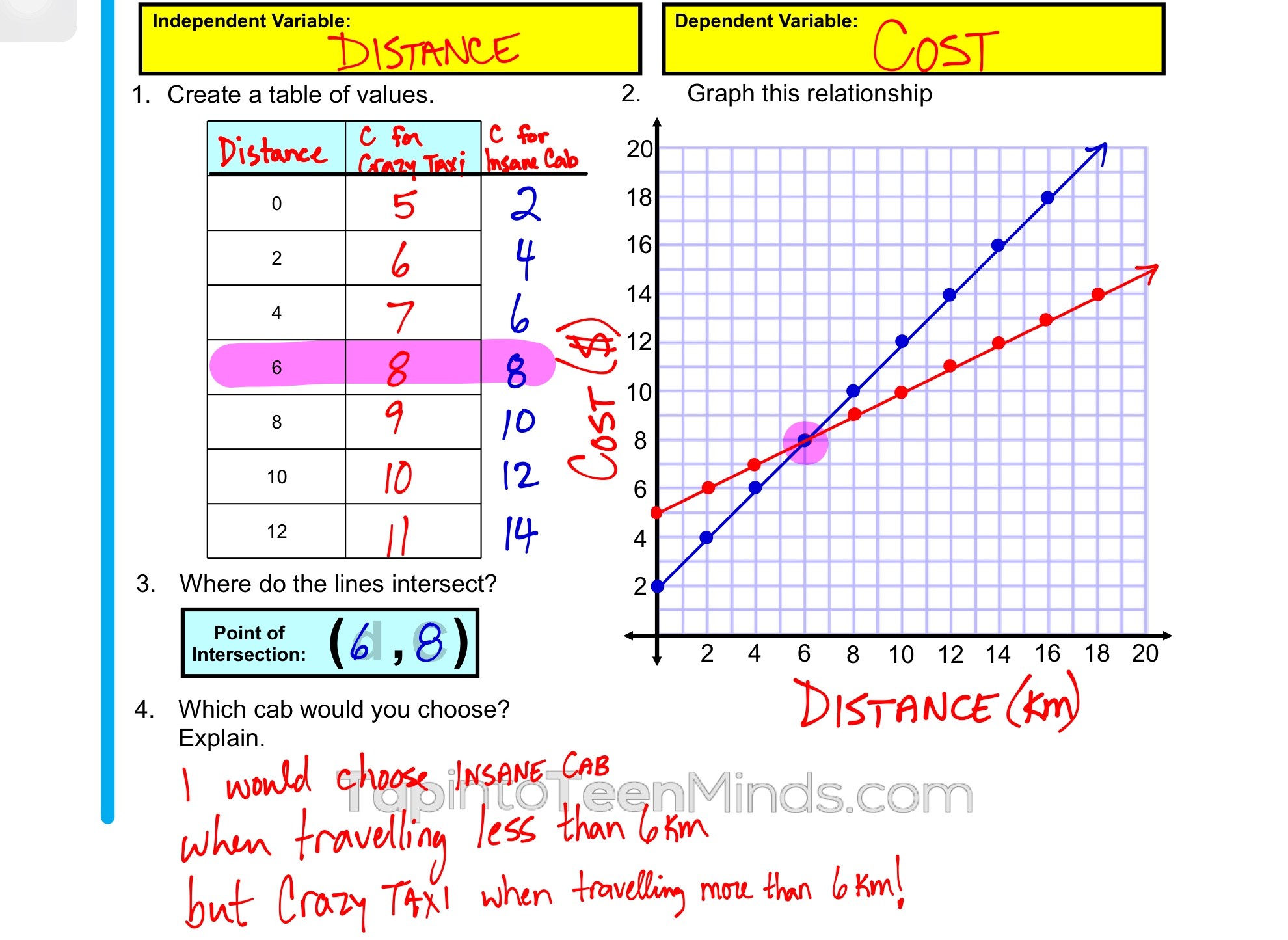
Students then used that information to create a table of values and graph in order to identify the point of intersection:
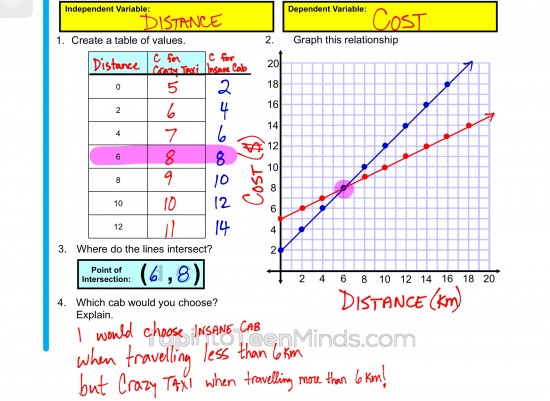
Nothing groundbreaking by any means.
However, at this point the students are feeling good and all can satisfy the original learning goal related to solving for the point of intersection graphically. They have identified the point of intersection as the point (6, 8) and we had a discussion about what each value, 6 and 8, represent in this scenario.
My plan now, was to have the class solve using the value of the dependent variable (C = 8) from the point of intersection in order to prove that the distance would be 6 km using both original equations:
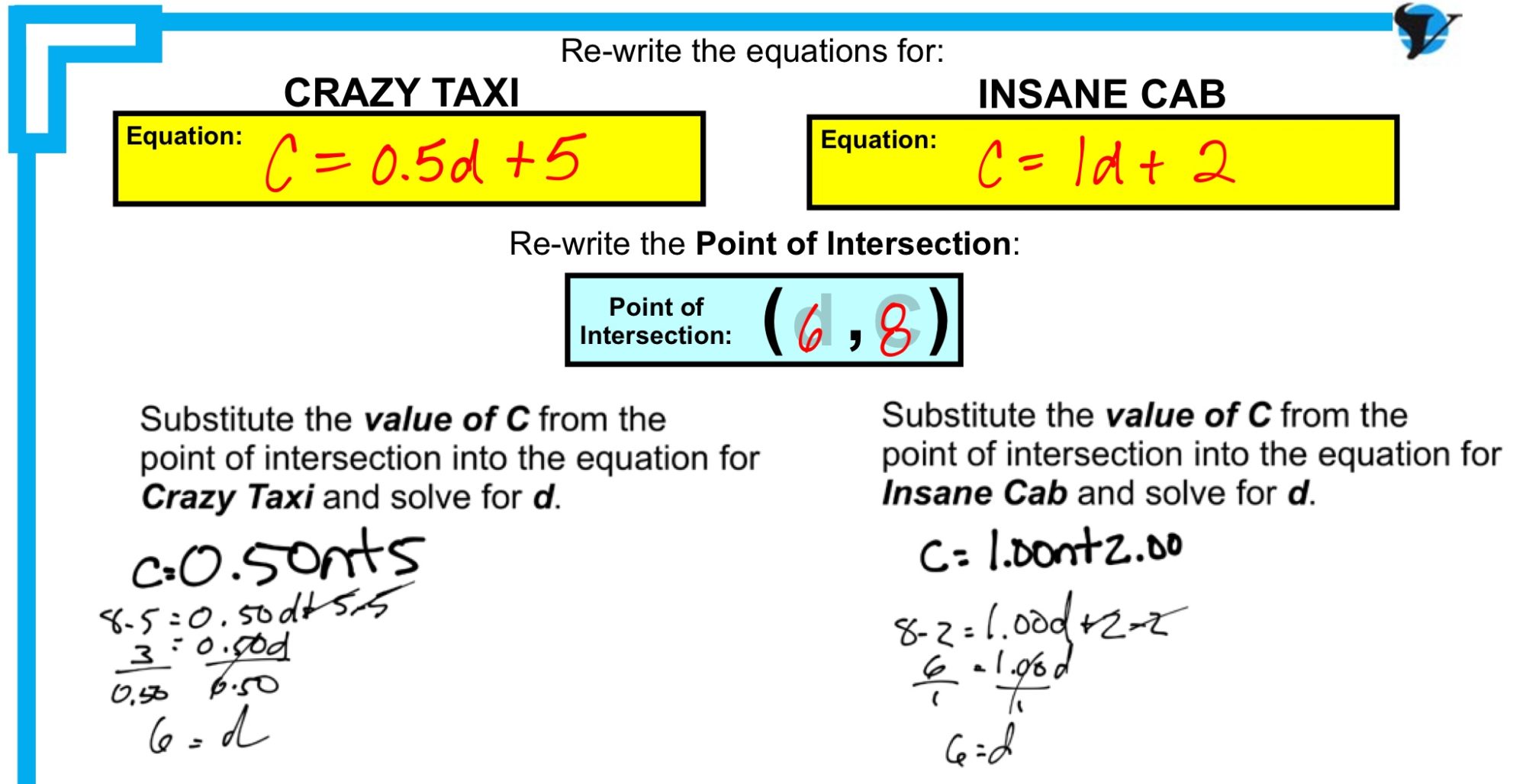
I think having the students create the table, graph and identify the point of intersection first gassed them. Engagement was definitely lost as we finally approached solving using the original equations for both taxi cabs. I suppose I should have predicted that students wouldn’t be entertained to find an answer they already had (i.e.: distance of 6 km and cost of $8).
Regardless, I moved on as planned by using an animation created in Keynote to introduce the idea of substitution:
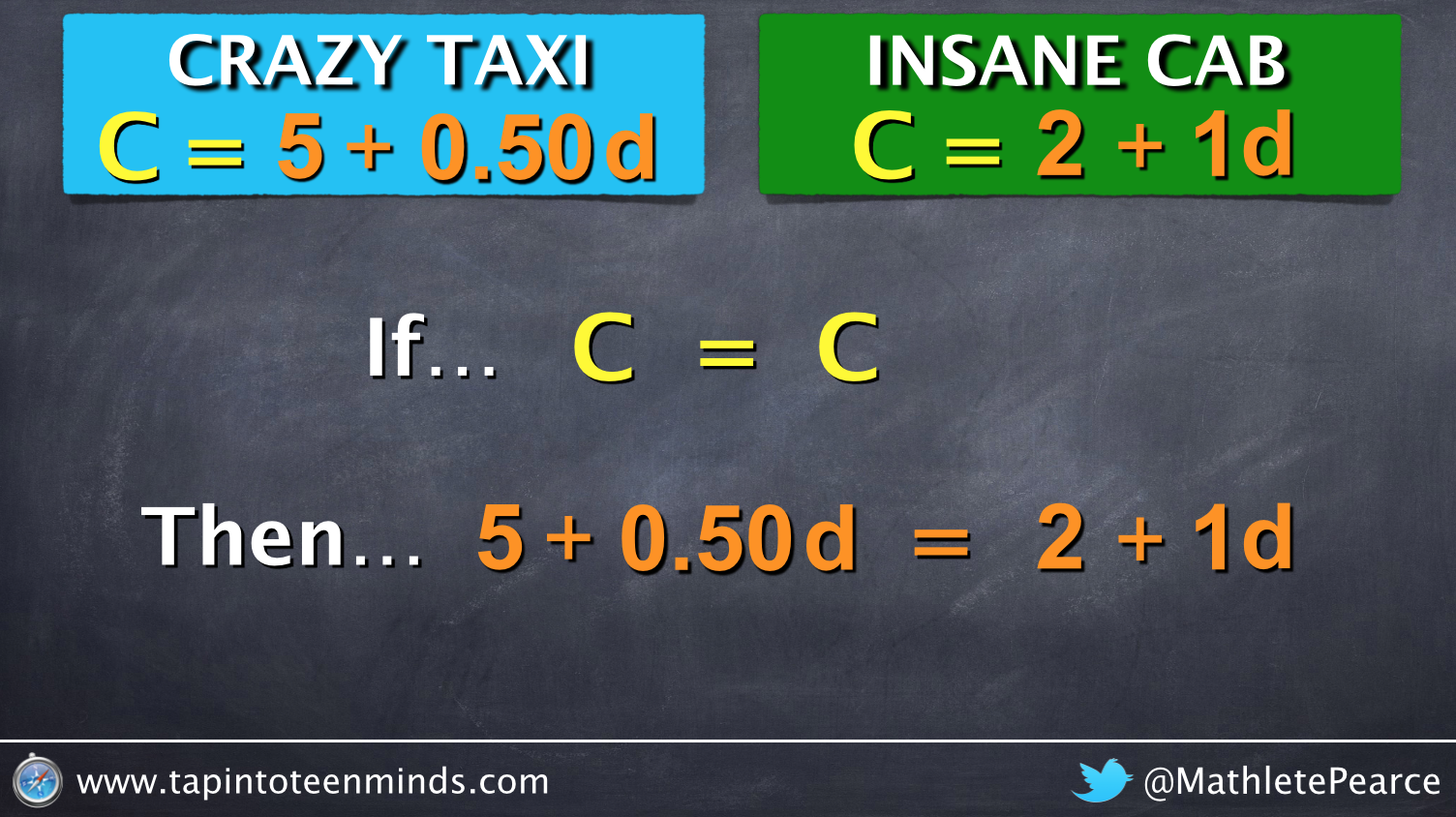
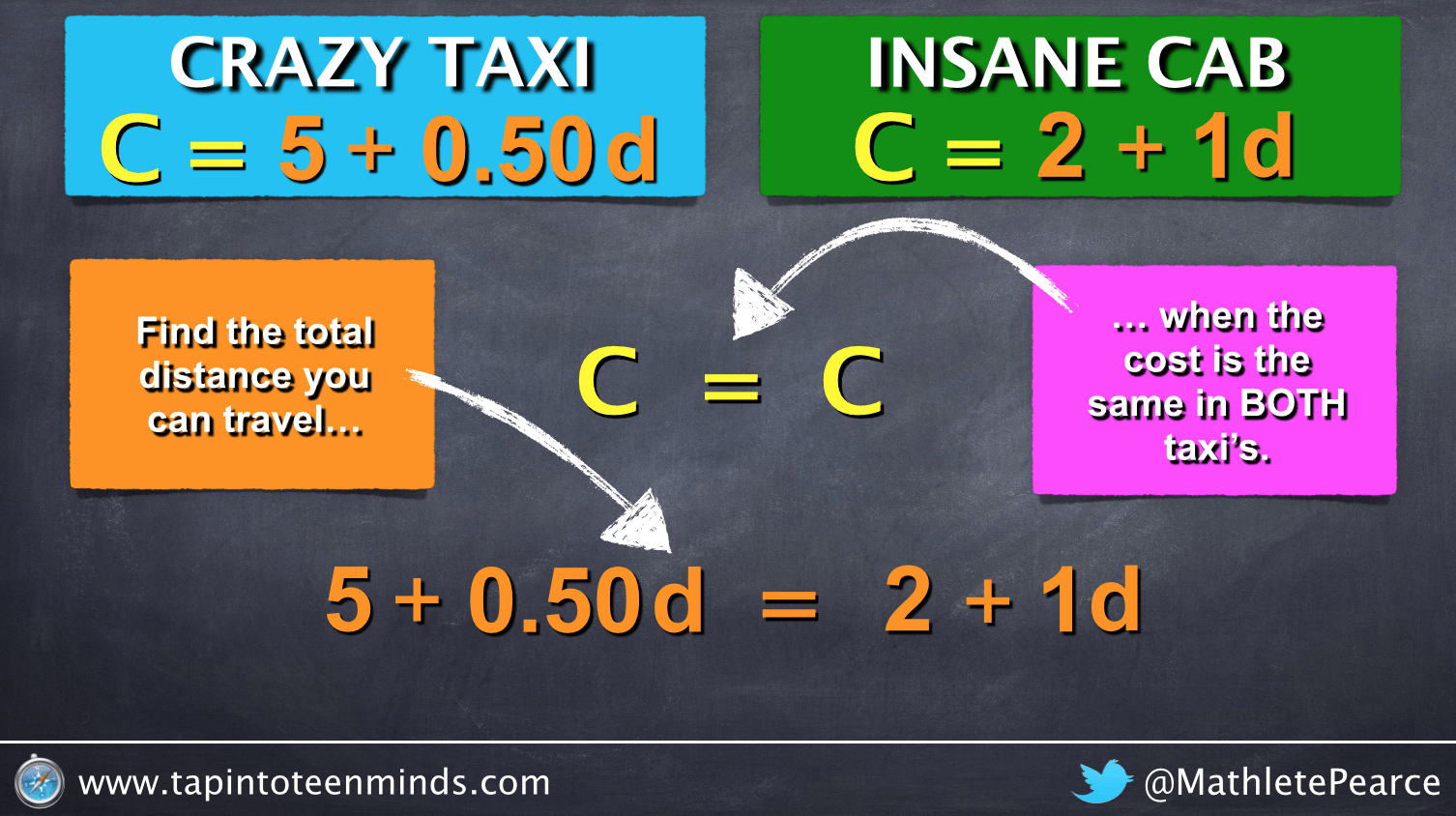
Students recognized that they were dealing with two equations that were equivalent at the point of intersection and we then managed to address the intended learning goal involving solving multi-step linear equations:

While this was an extension to the expectations outlined in the Ontario Curriculum for this course, I felt it was necessary to give students a reason to solve linear equations involving more than two-steps.
That being said, this was also the first time in a while that a student said “why are we doing this?”
“Why are we doing this?”
When a student comes out with the “why are we doing this” question, I know that I have work to do in order to add context to the problem and maintain the understanding of that context throughout.
In this instance, I went back and counted how many words/numbers/terms/points/etc. were required to find the solution via substitution:
I counted 28, which included some items that were not required, but added for clarity.
I then did the same for the table and graph:
I counted over 60 items.
We discussed how algebra is intended to save us time and effort by using the language of math, but we first required an understanding of how it works. A few students argued that although the table and graph required more writing, they could probably do it in less time than using the algebraic approach.
Which is better?
I then asked:
Which is better: crawling or walking?
All students agreed that walking is better.
I followed up with:
Which is better: walking or biking?
They all agreed with the latter.
I then asked students to raise their hands if they remember getting hurt when they were learning how to ride a bike and how long it took them to become proficient. Many student hands were in the air.
We discussed how babies and young children don’t have a fear of failure, but somehow we develop this fear as we get older.
Imagine you gave up on biking because you couldn’t do it right away? It’d be a shame if we gave up on math simply because we had to put some hard work in and fail a few times to understand it.
Working to ignore this fear of hard work and the possible failures that result is a major focus I try to embed in my lessons.
While this “work-in-progress” lesson didn’t produce the “ah-ha” moments I was hoping for, it did give me an opportunity to help my students grow by moving a little bit further away from the fixed mindset that many bring with them into my classroom.
As for this lesson, I’ll go back to the drawing board and attempt to maintain the context offered early in the problem, but lost once algebra took over. Suggestions appreciated in the comments…
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog


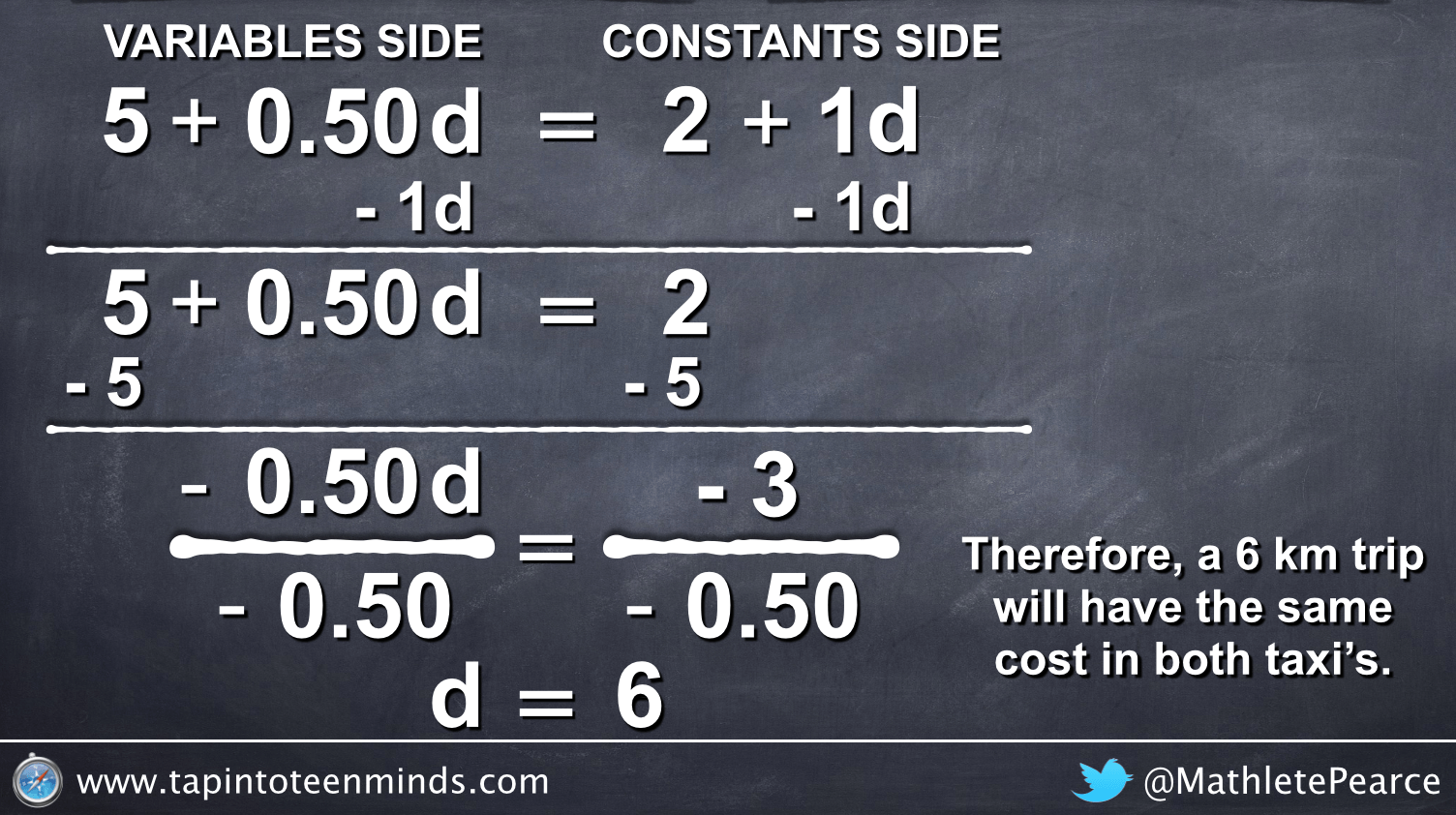
I’d hardly call this extension a “lesson failure” – kudos to you for, at the very least, exposing students to upcoming mathematics a bit early, so they’re familiar. Next time they might say, “I remember doing this before… with that taxi problem!”
I thought it might be a bit harsh to use the word “failure” in the title, but decided that it is important for us to look at failure as a positive instead of a negative. Most use the word to suggest that effort put into something (i.e.: learning) was useless when in reality, we need those failures to help us get better. We can even break down what most would consider a “good” or even “great” lesson into pieces where there were some excellent things going on as well as little failures along the way.
Could I have worded that question better? Did I miss an opportunity to let the kids talk it out? Focusing on these small failures and celebrating them is what will allow us to get better for next time.
I hope that with every new idea we try will help students to better understand and value the math we share with them – regardless of how smoothly things played out in the classroom.
Thanks for stopping by!