Unpacking an Effective Mathematics Lesson
When it comes to teaching mathematics, we often hear about effective strategies that could be useful during a lesson, but there is little talk about what actually constitutes a complete and effective lesson from start to finish.
In the following video (or jump to the summary below), I break down the 3-part lesson into 4-parts:
3-Part Math Lesson
In Ontario, John Van De Walle‘s 3-part math lesson has been promoted from the Ministry of Education to the districts, districts to school administrators, and from administrators to teachers. Despite efforts to provide resources for teachers, often times, guides provide only an outline of the lesson framework or a relatively basic example of what it may look like in the classroom. If a lesson example is provided, I’ve noticed the topics are geared towards primary or junior grade levels and the actual problem to be solved does not spark curiosity. Some examples of 3 part math lessons can be found here, here and here.
Just like a game of telephone, the message can get distorted as it moves down the line.
Common Interpretations
By the time the “3-part math lesson” message reaches the teacher, what is interpreted could easily look like the following:
- A 3-part lesson is an effective way to teach math.
- The 3-parts are named minds on, action, and consolidation or before, during, and after (or similar).
- Minds on is like a warm-up to the lesson.
- Action is where students learn the new concept.
- Consolidation is where we take our new learning and summarize it/practice.
There are some problems, though.
Many teachers walk away without a clear understanding of what this should really look like in the classroom. Some believe they are “essentially” delivering a 3-part math lesson because they already do a warm-up problem, deliver a lesson, and students consolidate their learning (i.e.: do practice problems).
Other teachers are working hard to improve engagement in math class by using 3 Act Math Tasks in the style of Dan Meyer, but are using them only near the end of a unit. I think waiting until all of the learning goals for the unit have been delivered with traditional, context-less problems is a missed opportunity to engage students throughout the learning process.
Because of these misconceptions and others that may surround the use of the 3-part math lesson and missed opportunities when integrating 3 Act Math Tasks, I will deconstruct an effective 4-part lesson structure into finer parts and model what this might look like in a middle years/intermediate math classroom.
The 4-Part Math Lesson
What I find is missing most often from most 3-part math lessons is the inquiry/discovery portion that should be embedded within the action/during phase. This is why I think it is really important that we break down the action/during portion into smaller parts:

Let’s jump into each part.
Part 1: Minds On
Like in a 3-part math lesson, we begin with a minds on. This may take 5 minutes some days or could take up to 25 minutes on others. While most are clear that the minds on/before phase is a warm-up, the biggest misconception I encounter is that it is any random problem to start the class off. John Van De Walle‘s 3-part math lesson suggested that the minds on promote activating prior knowledge in order to:
… get the students to be cognitively prepared for the lesson problem by having them think about ideas and strategies they have learned and used before. The teacher organizes a revisit to a concept, procedure or strategy related to the lesson’s learning goal.
Sketch of a Three-Part Lesson. Ontario College of Teachers. March 2010.
Extending what John Van De Walle suggests, we should also attempt creating a minds on that extends the context used during the previous lesson to help scaffold us slowly towards the new learning goal for that day. If we can also maintain the context from the previous lesson, that is a huge benefit that will help students build their new knowledge on prior knowledge.
In a recent workshop, I used the Stacking Paper 3 Act Math Task and solving problems with proportions algebraically as an example of the learning goal:


Part 2: Inquiry
After students have shared out, discussed and debated over solutions, the teacher then introduces the task for that day. Ideally, this task will maintains the same contextual scenario to allow students to easily leverage their prior knowledge while extending the previous learning goal to the new learning goal for that lesson. Making every effort to ensure the tasks offer real world context via a 3 act math task or similar will maximize the effectiveness of this part of the lesson.
The task used for inquiry/discovery is the most important part of a 4-part math lesson. The overall effectiveness of the lesson is closely related to how well this part is planned. A well designed inquiry/discovery task carefully sends your students down a path where they will ultimately “bump into” the learning goal along the way. When possible, use the same contextual situation from one learning goal to the next to allow students to more easily build their new knowledge through connections made to their prior knowledge.
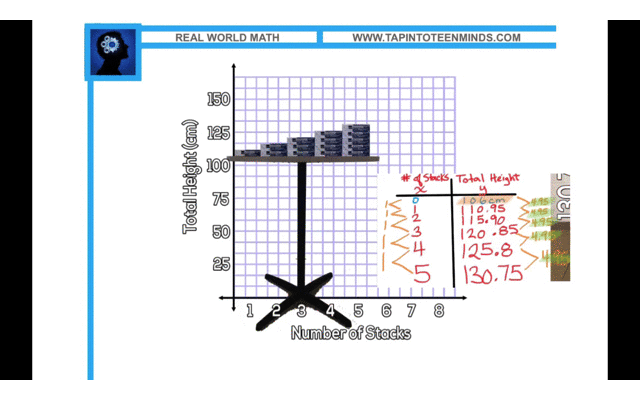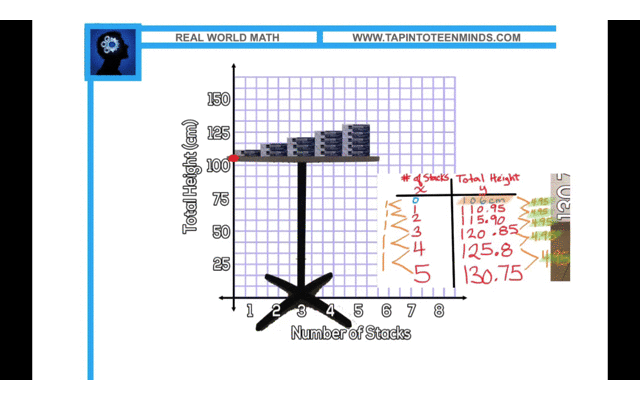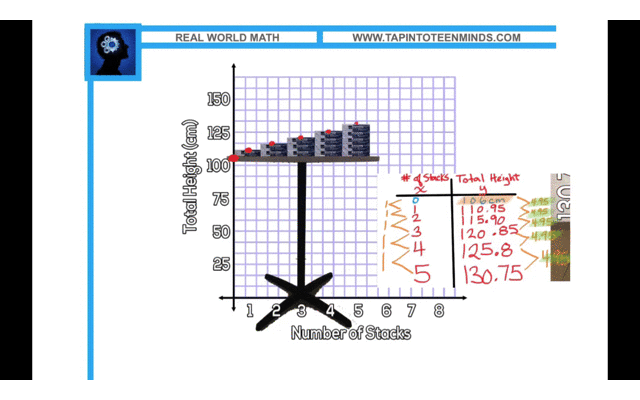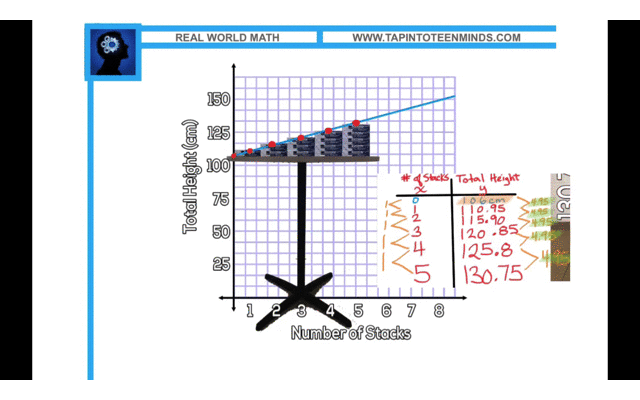
In the 4-Part Math Lesson video, I extend the Stacking Paper 3 Act Math Task to the Stacking Paper Sequel. In the first, students viewed a video of 5 reams of paper stacked on the floor and used information to determine how many reams it would take to reach the ceiling. The next day, during the inquiry/discovery part of the lesson, students see the same 5 reams of paper now stacked on a table with the total height given.
The question now becomes:
How tall is the table?

Here are some examples:
Solution Exemplar #1:


Part 3: Making Connections
After students have shared out, discussed and debated over solutions, the teacher then prompts students to chat with their elbow partner(s) to decide which method they feel is most efficient. When discussing as a class, the teacher should prompt students by asking questions such as:
- when the context changes, will using arithmetic/logic always be as easy as it was here? What if we remove all context?
- how long does it take to create a table? …a graph?
- is there a way we can create some steps that will allow us to do problems like this more easily?
As a group with the teacher leading as facilitator, connections between student solutions and the algebraic method or procedure related to the intended learning goal can be established.
After the desired learning goal has been established as a group, we then formally introduce the intended learning goal for this lesson:
Learning Goal:
I can determine the equation of a linear relation using algebra when given the slope/rate of change and a point.
We now solve the Stacking Paper Sequel Task using the algebraic method:

Part 4: Consolidation
The consolidation phase is where we begin to remove the context from the problem and move towards the typical types of problems you see in traditional textbooks and on standardized tests. It might seem as though you are moving backwards from great real world problems that pique curiosity and perplex students, but unfortunately, the types of problems students are currently expected to solve in traditional textbooks and on standardized tests are text-heavy and lack any meaningful context or purpose.
Now that students have an understanding of the learning goal and we have made connections from an authentic real world problem to the algebraic representation, students can use this knowledge to solve problems with little or no context.
Here is an example of a problem we could now use to consolidate the learning:
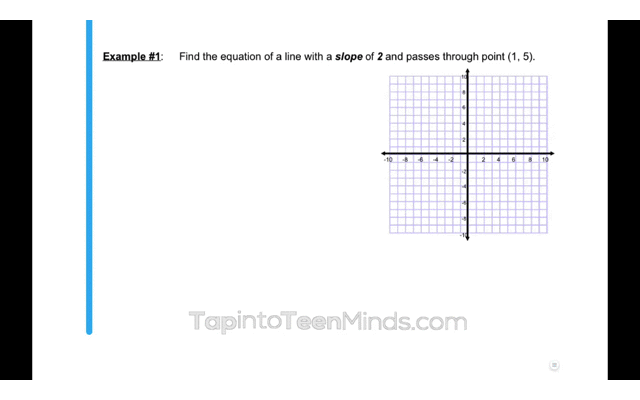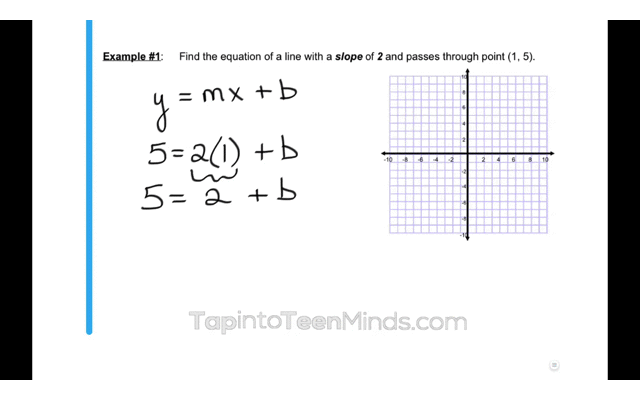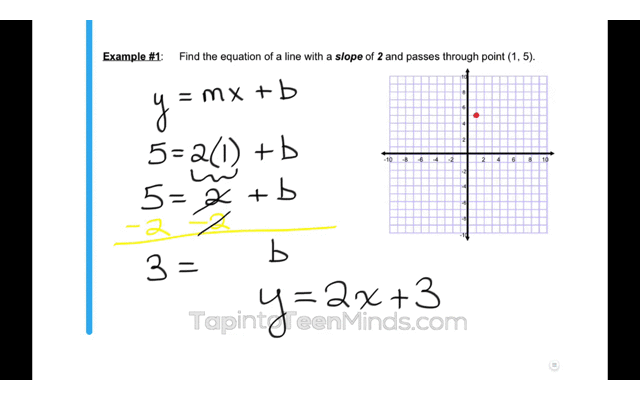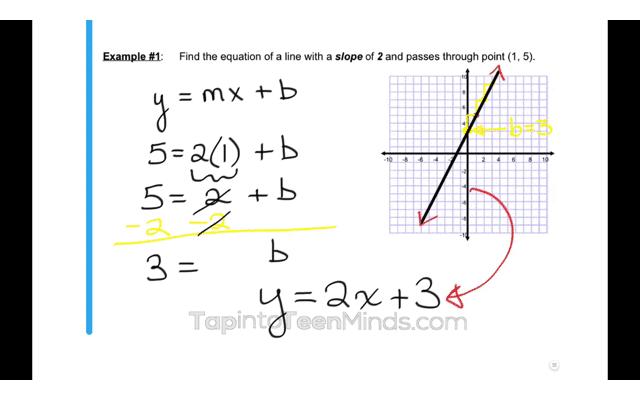
Upon completing these 4-parts of your math lesson, students should now have the understanding and confidence to do the necessary practice to master the intended learning goal.
The Next Day…
I mentioned earlier that building on the same context from each learning goal to the next can provide a huge benefit. In order to continue the deconstruction of this particular lesson, the task I would use for the Inquiry portion of the next lesson would be the Thick Stacks 3 Act Math Task. In this task, students are provided with an image of two stacks of paper on a shorter table and are given the total height of each stack on the table. Students are then to determine:
What is the height of this table?

Learning Goal:
I can determine the equation of a linear relation using algebra when given two points on the line.
In my experience, this can be one of the most challenging learning goals for grade 9 academic students until connections are made. This task allows students to make these connections quickly and in a seemingly natural way.
Here are some possible solutions to this task as well was the consolidation (i.e.: problem with no context) I would use for that lesson:
Grab The Stacking Paper Tasks Multi-Touch Book!
Have you tried the 3- or 4-part math lesson?
Would love to hear your experiences, both positive and negative, in the comments section!

