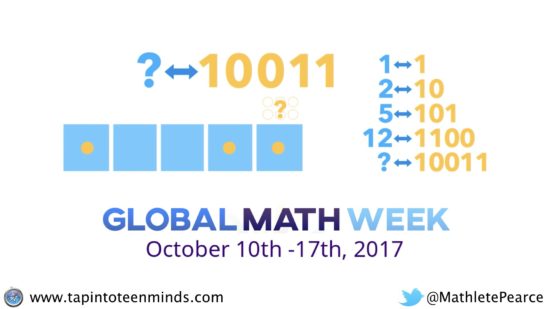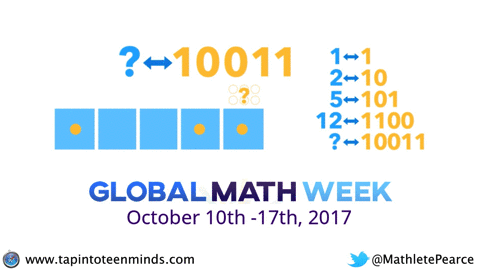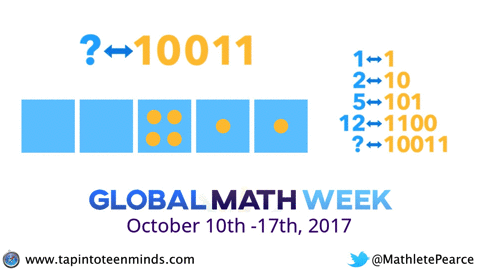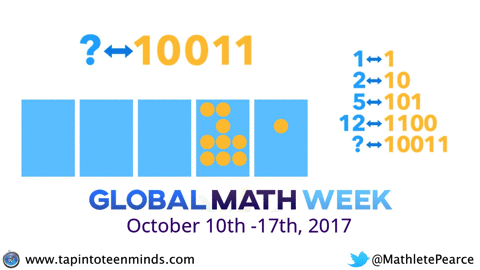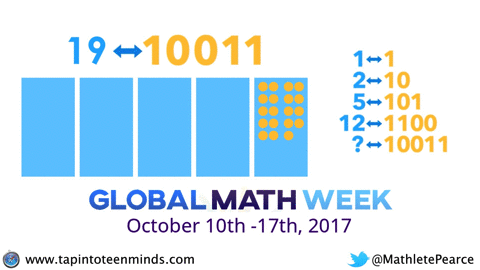Exploding Dots for Global Math Week

Let’s Get Over 1 Million Students Engaging in Joyous Math!

If you’ve ever checked out my 3 act math tasks, you will quickly notice that I am all about sparking curiosity in order to fuel sense making for our students. Well, Exploding Dots nails the curiosity AND sense making pieces of the puzzle and with Global Math Week coming up next week, what better time than now to jump right in!

It was only a few months ago when I really started exploring this idea called Exploding Dots, but I was immediately intrigued. Since then, I have fallen in love with this amazing story of mathematics that James Tanton and The Global Math Project are hoping to spread to over 1 Million students around the globe.

Why not join the rest of the world next week for a 15 minute exploration or days of math fun with Exploding Dots. Best of all, there are full technology, low technology and even no technology versions to enjoy! Registration is simple because it only involves a pledge of participation and you can do it in under a minute here.

Enough of me pitching this “joyous and uplifting mathematics experience for all.” Let’s get your feet wet!

DISCLAIMER: READING ON IS LIKE SPOILING THE END TO A MOVIE. I highly recommend just jumping into the first Exploding Dots activity (called an “Island”) instead of reading on. However, if you aren’t going to take the time to give it a shot, I’d rather you read in order to share this great experience with your students.

Start By Sparking Curiosity

Watch this video.

In the “silent solution” style video, you are exposed to the “2-to-1” machine (written 1 <-- 2) and are left hanging at the end when they ask you to figure out how many dots would be required in the rightmost box to have a code of 10011.

So. Give it some thought. Maybe draw it out?

It’s never too late to dive into Island 1 and see if playing with the “1 <– 2” machine can help construct some understanding AND I promise you’ll have fun doing it.

For those of you who still won’t go and just dive in to play with the Exploding Dots app, let’s have a closer look at the first island, Mechania.

Island #1 – Mechania: Exploring The Dot Machines

I’d like to share a quick video at the beginning of the first Island, called “Mechania” to assist you with your exploration.

After watching the video, the Exploding Dots app has you jump into the action asking you questions that press you for understanding. It might seem tricky at first, but remember: this activity isn’t about finding the right answer; it is about sparking curiosity, using strategic competence and building a productive disposition towards mathematics.

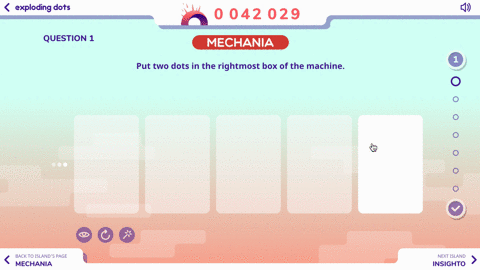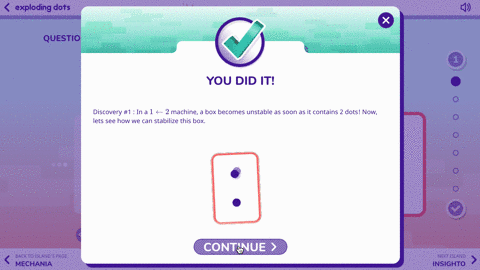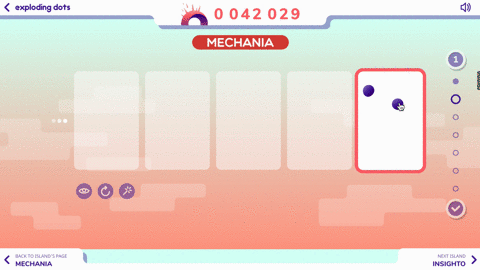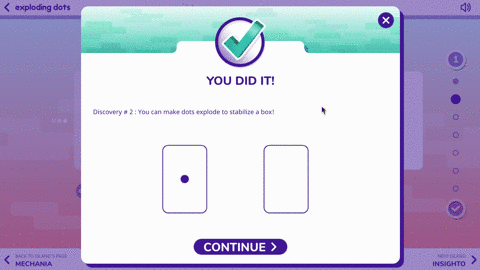
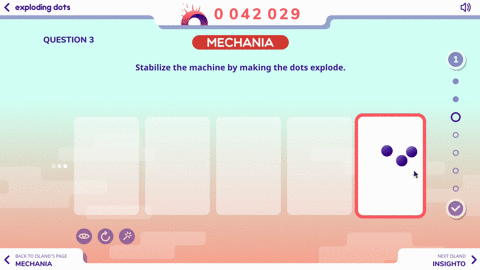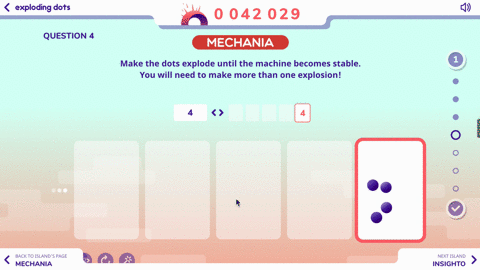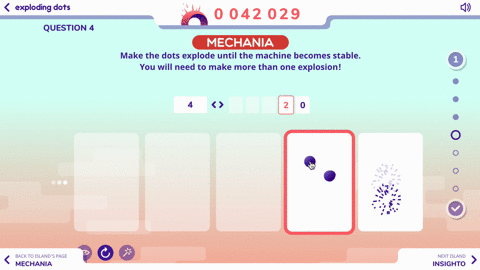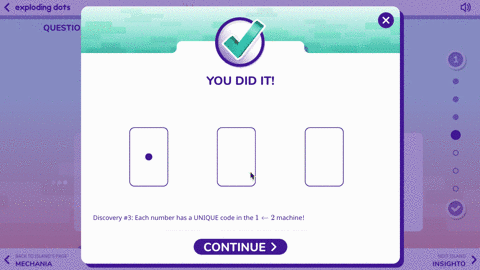
Here’s a look at the first two questions:

Pretty simple, right?

The Exploding Dots app starts with a very low floor and has an extremely high ceiling.

Here are the next two questions to explore with the 1 <– 2 machine:

Before you know it, you’ll be tacking problems like this one:

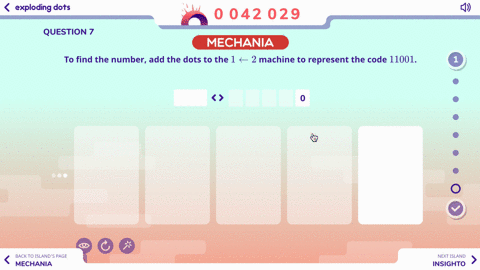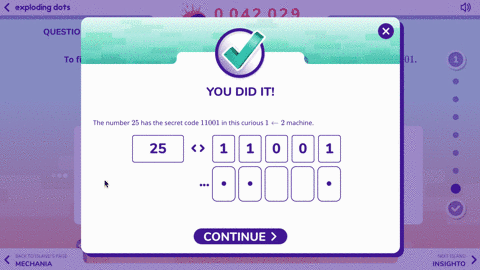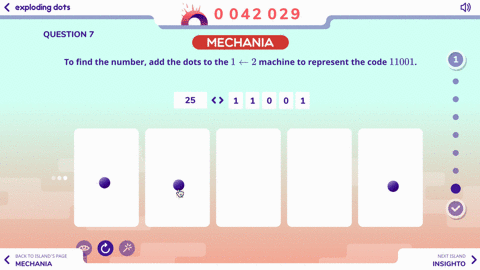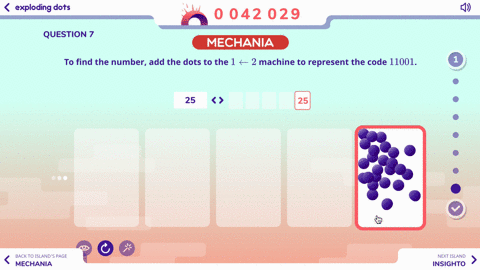
Wait a second. Didn’t the question posed in the video at the beginning of this post look an awful lot like what we just did in the previous question?

Here it is again:

Do you think you can try it now? Go ahead. Take your time.

Heck, why not try the 1 <-- 2 machine in the Exploding Dots app to help you?

Here’s a strategy someone might use to answer the question:

Can you find a more efficient way?

What’s The Big Deal About the “1 <-- 2" Machine?

Aside from the fact that curiosity is surging, strategic competence is spewing and productive disposition is oozing at all time levels, you could consider exploring how the 1 <– 2 machine helps computers work. While some may have picked up that the 1 <– 2 machine is the same language that a computer uses, many others may not. The base 2 number system – a series of “on” and “off” digits – is extremely important in computer science. It is the language computers speak!

While you might think the fun is over, it’s just begun as you continue through this activity to explore the 1 <-- 3 machine as well as the 1 <-- 10 machine. Something you may notice rather quickly with the 1 <– 10 machine is that it is the “base 10” number system; the standard number system we use in our everyday lives.

A Quick Look At Each Activity

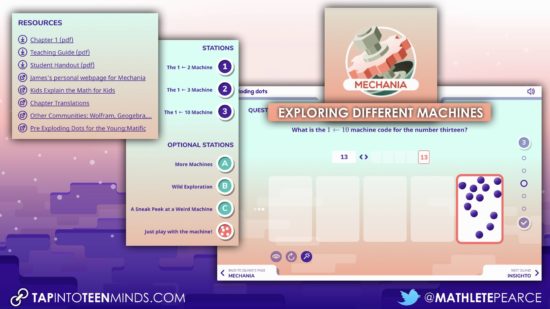
Once you arrive at the Exploding Dots landing page, you’ll notice that there are quite a few activities (called “Islands”) for you to explore. I believe the best experience would involve students diving in from the beginning, however it might be useful for you to see where students will eventually land as they traverse through each of the Islands.

Since we explored the first island, Mechania in detail above, let’s take a quick look at each of the remaining 5 islands that are active on the Exploding Dots website to expose you to the other mathematical connections that can be made from Kindergarten through Grade 12.

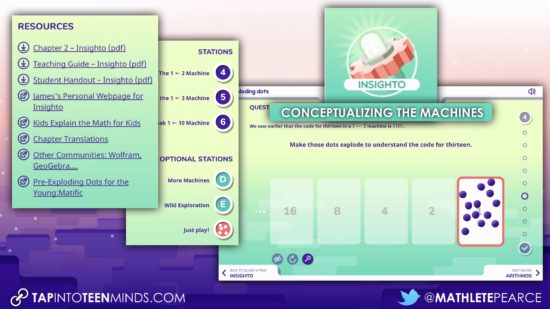
Island #2 – Insighto: Conceptualizing The Dot Machines

After students explore and discover in Mechania, students will be brought to Insighto to begin unpacking the conceptual pieces that make the different dot machines work.

Island #3 – Arithmos: Addition and Multiplication

After building some of the conceptual understanding from the Insighto Island, students will be brought to Arithmos to begin applying our understanding of the 1 <-- 10 machine to addition and later, multiplication. The logic students can build using the dot machines really helps them grasp an understanding of place value and why standard algorithms work.

Have a look at a sample of addition:

And later on, multiplication:

As students work through the Island of Arithmos, they will eventually arrive at commonly used or “standard” algorithms for addition and multiplication wrapped up with a nice bow of conceptual understanding.

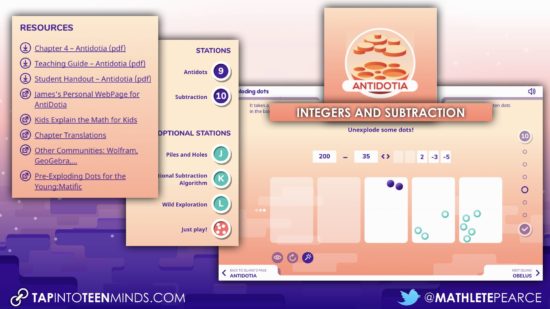
Island #4 – Antidotia: Integers and Subtraction

What? Integers before subtraction?

YES! When students arrive on the Island of Antidotia, they will immediately be introduced to “dots” and “antidots” which intuitively build an understanding of integers prior to looking at subtraction. This is because the concrete and visual representations for both will look identical.

Students will eventually be led to standard algorithms we commonly see in elementary school for subtraction while also building an understanding of integers and the zero principle.

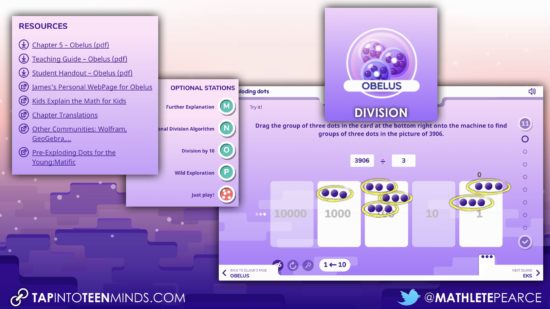
Island #5 – Obelus: Division

Get ready to look at division in a brand new light. Imagine possibly getting to a point where you could pretty accurately divide large numbers by focusing just on digits in each place value column.

While I love the entire exploding dots experience, I think the conceptual understanding this particular activity builds in students around division alone is worth the time and effort!

Island #6 – Eks: Multiplication and Division in Any Base

Ok, secondary math teachers. This is the island you’ve been waiting for. This is the reason why you put in the time and effort with your senior secondary math students with the Exploding Dots experience.

Have you ever imagined multiplying or dividing in any base in a way that was not only procedurally possible, but also conceptually understandable for students?

Well, here’s your opportunity. Students can play with big, long, BEAUTIFUL polynomials and they can quickly discover how to divide, handle remainders including The Remainder Theorem and multiplication of polynomials.

Ready to explore?

Join Us During Global Math Week!

If this blog post hasn’t inspired you to join us during Global Math Week with Exploding Dots, then clearly I have done you wrong.

Take the time to register your class and spread the word with your colleagues.

Together, we can reach over 1,000,000 students!

Or, 0111011100110101100101000000000 students if we use the 1 <– 2 machine.

Or, 2120200200021010001 students if we use the 1 <– 3 machine.

Or, 323212230220000 students if we use the 1 <– 4 machine.

Or…

Ok, I think you get the point.

Read More From The Blog

---

Not What You're Looking For?

Search By Criteria: