UPDATE: Tuesday March 4th, 2014
I introduced the concept of distribution using this problem today. I added the solutions below, so CLICK HERE to jump to the bottom if you’ve read this post previously!
It is no secret that I am a big fan of Dan Meyer’s 3 Act Math Tasks for the immediate interest and attention you receive from your students. Using tasks shared by Dan and other Mathletes from around the globe can save you tons of time in preparation, but it cannot save you the time required to use the tasks effectively in class. Don’t get me wrong, I think making math real is worth the additional time spent, however I don’t think Dan intended for the 3 Act Math Task to be used daily.
Making Math Real Can Be Simple
One of the most valuable changes in my teaching practice I have gained since hearing Dan Meyer present at the OAME 2012 Annual Conference in Kingston, Ontario was analyzing simple questions I have used in the past in order to connect them to something in the real world.
Take the following question that I typically used during my lesson that introduced the Distributive Property in grade 9:
Thinking back to when I first began teaching grade 9 academic, I probably was just trying to “get it done” to ensure the students had enough to practice. Quantity over quality was definitely the motto and I am now realizing that it should really be the other way around. When you are an inexperienced teacher, the worry of students running out of work to do can be scary. Now, I know that the Less is More approach is definitely better and I am slowly trying to take the chance to get there.
This particular unit is one that students typically struggle with year after year. Along with my commitment to add algebra tiles and other visual manipulatives to the unit, I am also trying to make the math real without necessarily creating a 3 act math task.
Could it be that the math isn’t as hard for the students as trying to bring themselves to understand “why” we are trying to solve the problem?
Tomorrow, I’ll wrap up my unit on polynomials and try to introduce the use of the Distributive Property using the “old” question with a “new” real world connection:
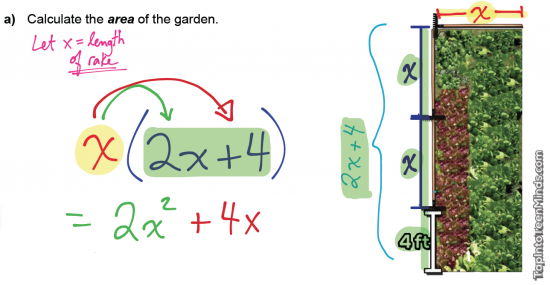
Mr. Pearce has a vegetable garden in his backyard for growing hot peppers, along with other vegetables. Whilst he had to enlist the help of somewhere like this Happy Valley tree removal service to remove all of the unwanted trees, he was determined to make his vegetable garden the best he could make it. And this would take a lot of hard work. He needs to buy his plants and some fencing to keep out the rabbits. For that, he must first choose what plants he requires, along with hot peppers, and probably learn how to grow bell peppers or any other vegetables. He must also determine the area of the garden and perimeter before making any purchases for vegetables or fencing. Unfortunately, he only had a rake and 4 feet worth of landscaping bricks to measure, which definitely won’t help him when it comes to fitting these stone veneer panels for exterior use onto his home as he won’t be able to accurately determine how much of each material he will need. As that is for the future, will he be able to find a measurement whilst only using these materials?
a) Create a simplified expression for the area of the garden.
b) Create a simplified expression for the perimeter of the garden.
c) Find the area and perimeter if the length of the rake is 4.5 feet.
Here’s a higher resolution version of the image, if you’re interested in using the problem in your own classroom:
Solutions to the Problem
After a week of using algebra tiles to introduce the idea of expressions, simplifying expressions by collecting like terms, and adding/subtracting polynomials, I used this problem to introduce the Distributive Property.
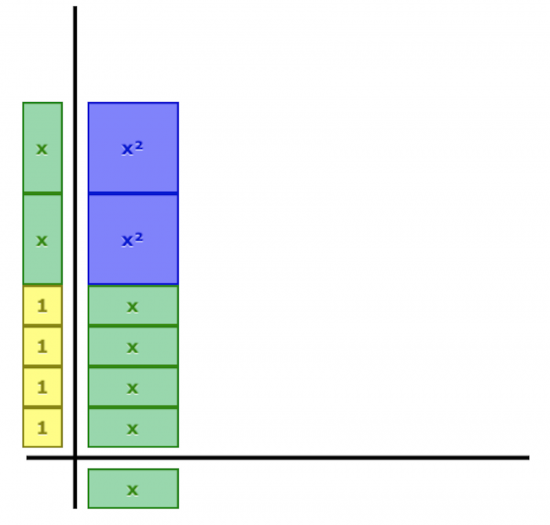
To my surprise, students actually used an approach similar to what we had been doing with algebra tiles previously in the unit. Many students suggest they dislike the algebra tiles, but I don’t think they realize their value as is apparent to me in this solution:
Some students weren’t too sure about what their peers meant by the rake-squared, but it was clear to me that they were really understanding what we have been doing with all of these x^2, x and unit tiles all along.
After solving the problem using the visualization, we then proceeded to look at it another way in order to discuss distribution:
While we plan to review our learning goals from this unit tomorrow and have an assessment on Friday, I think that spending some more time this unit would be ideal. It’s the day before March Break which is the Canadian version of Spring Break. It’s basically the time when the older students spend hours searching for legit fake id sites before spending the week partying with their friends, not that I ever engaged in such activities (*rolls eyes discretely*). Anyway, I will have the assessment and use it as an opportunity to provide students with feedback. If we still need some more time, we can revisit upon our return from the break.
Tomorrow, I intend to take this garden problem and model it using algebra tiles to discuss both methods again using something like this:
Your turn…
What do you think? How do you make questions “real” when you don’t have time to add a 3 act math task to the repertoire?
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog