A couple days ago, I wrote a post explaining that Making Math Real Doesn’t Have to Be Difficult. In the post, I attempted to make connections between an algebraic representation of the area of a rectangle involving a variable and a visual of the same scenario using a method based on the use of algebra tiles for distribution.
In previous years, I would have simply provided students a diagram of a rectangle with dimensions labeled.
Students would then write an algebraic expression that would require the use of the distributive property to expand and simplify the expression:
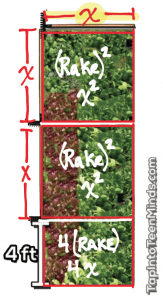
x(2x + 4)
= 2x^2 + 4x
This year, we approached the problem visually prior to introducing the algebraic approach with distribution by splitting the area up into smaller, more manageable “chunks.”
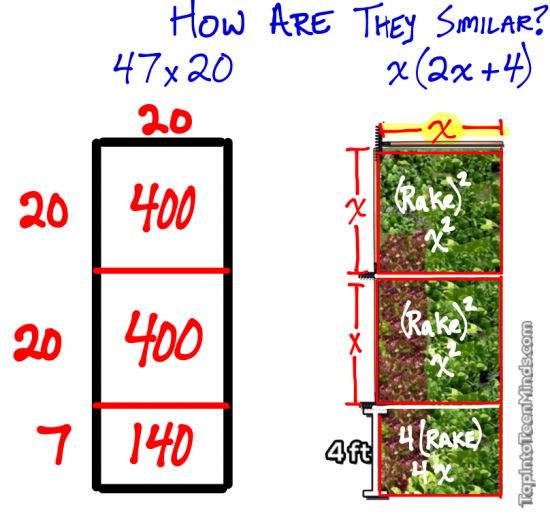
While most students are comfortable with a question like this as a reasonable point of entry, it might be wise to make some connections to their prior knowledge in mathematics. A fellow “Math Tweep” was kind enough to share an easy way to get kids connecting this visual representation of a concept I traditionally would introduce in a very abstract way. Helene Matte (@mmehmatte) sent me a link to a screenshot of the same strategy, without the algebra.
Helene has related basic multiplication that students most likely are learning through an algorithm to a visual representation that could also be connected to a much deeper concept of area with an unknown value involved in the length and width. While it might seem obvious after viewing the screenshot, I completely overlooked this as an option to make the entry point even more accessible for all students in my class.
Thanks to Helene for sharing her useful strategy that I will definitely be using after March Break to continue our exploration of algebra from a visual perspective. Expect more involving algebra tiles and visualizing algebra in the coming weeks!
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog