
Recently, I’ve been on an Algebra Tile kick to try and address an urgent student learning need I see in my classroom and across the district. Even students with higher marks in math don’t necessarily understand what it is they are actually doing; simply memorizing procedure and replacing the numbers from the example copied in class is usually enough to get by.
Shortcuts Before Taking The Long Route
While I can’t know for certain, I believe that many students are asked to use algebra in math class prior to understanding enough about number sense to use it effectively. Think of it like this:
My friend Joel has a cottage in the sticks just outside of Tobermory, Ontario and my wife and I (and now Taliah, too) have been making the drive for the past six years. If you’ve made the drive from Windsor, you’d know that there really isn’t a direct route. As you get closer to the cottage, roads begin to wind, you have to make more turns, and ultimately it can be very difficult to know where you are.
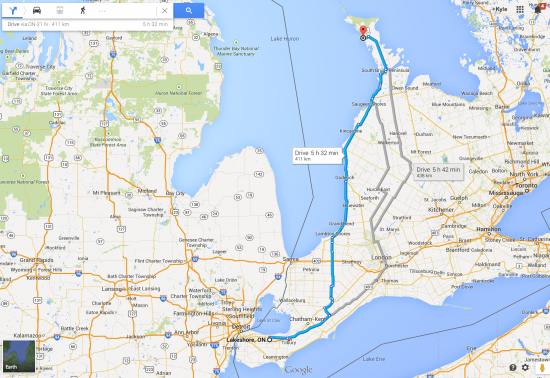
May Not Be Fun, But You’re Less Likely to Get Lost
For the first three years, my buddy sent me the “long” way which meant about 15 minutes added on to a 5+ hour car ride as we would head out to the highway closer to the town of Wiarton (yes, where the Groundhog lives). This route had the most signage to ensure we would have the best chance at getting there without much trouble.
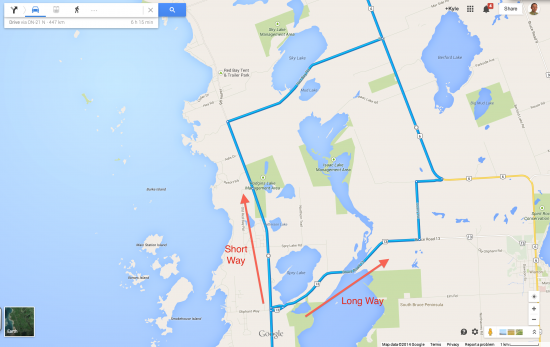
Understanding Leads to Shortcuts, Tricks, and Timesavers
After driving to and from to the cottage a handful of times, I asked Joel to explain directions to use the shortcut as we sat by the fire one of the nights. The only real problem with the shortcut was the lack of signs and landmarks to determine when you should turn to head up to the highway. Because we had travelled to and within the area so much, I had enough background knowledge to assist me if I missed a turn. Backtracking to correct course was easy enough because I had the confidence to get myself out of any jam I could put myself into.
Math is like a trip to your buddy’s cottage…
Understand how to get there the long way before trying to take shortcuts.
Most notation in math was created to make things easier. Algebra is the short form to writing mathematics and can assist us in solving larger problems more easily. Unfortunately for most, algebra is introduced before a deep understanding of the concepts are developed and this can lead to problems later. Due to a lack of understanding in the area of algebraic reasoning, teachers often develop even more shortcuts to help students “get it.” In most cases, I think these shortcuts simply help the student appear to do well on assessments, while simply masking the problems that exist underneath.
Don’t Teach Tricks, Teach Understanding
I’m definitely guilty for creating and modelling “tricks” to help students easily memorize the steps to solve a problem. Cross multiplication (solving proportions), magic circle (proportions), y-thingy thingy (proportions), magic stairs (unit conversions), switch sides/switch signs (solving equations), SOH-CAH-TOA without any real explanation as to “why” (primary trigonometry), and many others have been used in my classroom, but I am done with them. If students want to develop rules, tricks, and shortcuts together as they see them emerge from the inquiry process and their own deep understanding, then I’m all for it. However, simply providing a “rule of thumb” to promote memorization is something I can no longer bring myself to do.
Have you ever used rules, tricks, and shortcuts over the years? What are your thoughts after your experience? See you in the comments!
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog

Kyle, we like this…posted it at http://www.facebook.com/commoncoremathresources
Thanks for the feedback and for sharing! Checked out your page and it has some great resources!
Love the analogy Kyle! Deep understanding is so key. It’s great to see your blog and the many ways you make Math real and accessible for students. I think we need to get students interested in Math in order to change the culture away from tricks and toward an appreciation of the long way.
Can I use that image and give you credit?
Hi Steve:
I think we are getting better at understanding what students need to make math interesting and accessible, but it will likely take many years before we see a shift away from intimidation.
Feel free to use the image. A link back would be appreciated! Cheers!