Picture the Math Before You Do The Math
The second unit in my MPM1D Grade 9 Academic Math Course is typically the portion of the course students struggle with the most and coincidentally the most boring to teach.
Why do students struggle with this unit? Well, it deals with communicating math algebraically.
Why is it boring to teach? Well, it deals with communicating math algebraically.
Knowing both of these facts for the past few years I have been teaching this course, it never occurred to me that maybe there is a correlation here. If it’s boring for me to teach, it’s gotta be even more boring for the students to learn. If it’s boring for the students to learn, then can I be surprised when students don’t have a deep understanding of the concepts? If we assume that we live in a perfect world where all students want to maximize their potential, then there probably wouldn’t be an issue. Fortunately, this perfect world doesn’t exist.
No, that’s not a typo.
I’m happy that we don’t live in that perfect world where I could go on teaching boring concepts in a boring manner. What would be the point of that? Would I really want to get up for 30+ years to teach the same boring concept with no context, discussion, or excitement? I can’t speak for you, but I think I’d poke my eyes out.
As you’ve read in my previous posts, I really wanted to dive into making this unit as visual as possible. Many would argue that a best practice early in your course would be to give some sort of assessment to determine which of Howard Gardner’s Multiple Intelligences best suit each student in your course with visuals being one of them. In the past, I would argue that I was strong in Logical/Mathematical intelligence, but weak in visual intelligence. I am now realizing that this was likely due to my lack of exposure to visuals when learning math. Using algebra tiles throughout this unit is proving to provide students with a deeper understanding of the concepts and giving all students an entry point, regardless of their mathematical readiness.
Why this section of the unit sucked…
In the past, I setup my course to follow closely to the textbook I had used as a resource. This particular section introduced algebraic language such as constant, variable, coefficient, polynomial, degree of a term/polynomial, and many others in one shot. Rather than slowly introducing these new words throughout the unit, we would hit the kids with a big list of terms and show a few examples. Pretty boring stuff. I think my thought (and the thought of the textbook authors) was: “let’s get this stuff out of the way.” You know, like a bandaid. This approach made me dislike this lesson and I really didn’t have any tricks up my sleeve to make it any more interesting.
Using Visuals to Make It Better
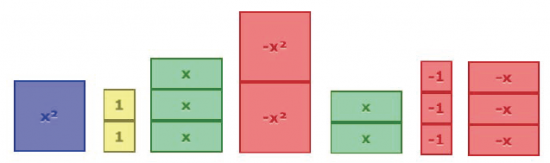
This time around, I scrapped fill-in the blanks, definitions, and the other ineffective tactics I was using and just tossed out some expressions like:
With elbow partners and as a class we would discuss patterns we see, attempt to make sense of what we saw, and slowly introduce some of the concepts I would typically introduce through definitions.
From here, we would identify some of the key concepts I wanted them to begin using throughout the remainder of the unit and course. The goal here is to allow students to get better at identifying an expression, coefficient, degree of a term, etc. but not necessarily have a formal definition memorized. The intended result is to have students begin formulating their own understanding of each concept in order to define in their own words when they are ready.
Here are a few of the other tasks I had students work on in partners to share with the group:
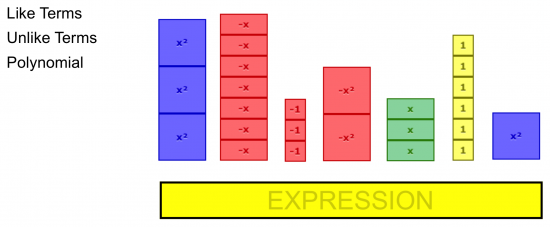
Identifying Like Terms and Polynomials
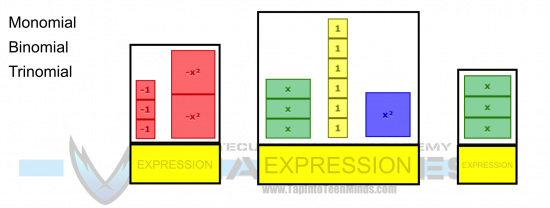
Naming Polynomials: Monomial, Binomial, Trinomial
Identifying Key Algebraic Concepts / Definitions
Developing a More Formal Definition of Each Concept and/or Term
Deepen Understanding By Extending the Discussion
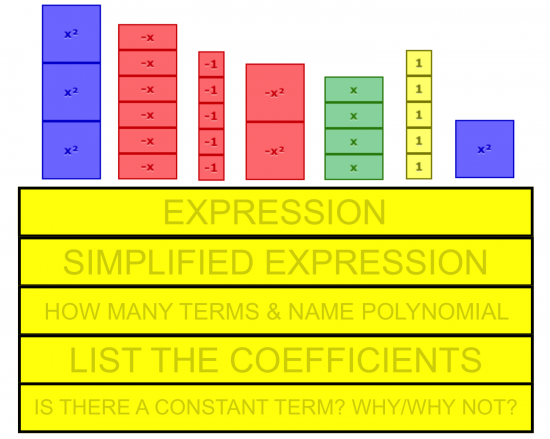
After consolidating some of our new learning, we can then jump into visual problems where students can begin to identify what simplifying expressions really means because they see the number of algebra tiles decreasing, beginning to understand that a coefficient is really a more “efficient” way to write out the expression rather than through repeated addition, and much more.
While the activities from class don’t necessarily bring too much in terms of context to the table (working on that for next time), here are a few of them for you to see:
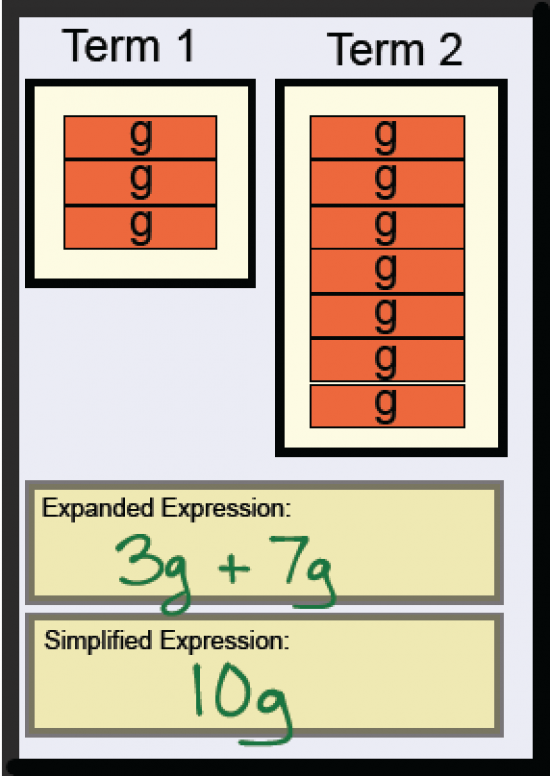
Basic Simplification / Collecting Like Terms
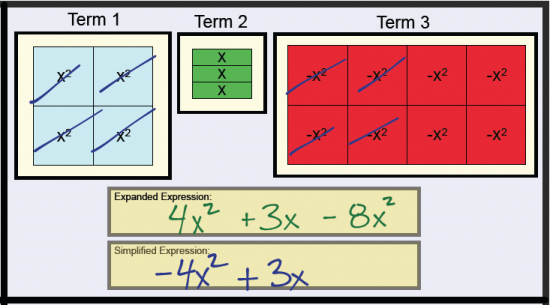
More Complex Simplification by Collecting Like Terms
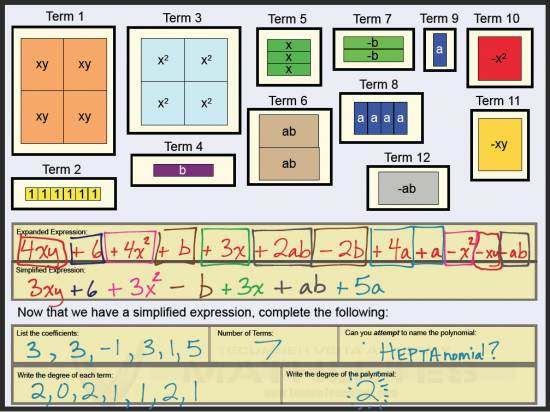
Applying Algebraic Terms and Concepts to Larger Problems
As mentioned in the previous paragraph, my goal for next year will be to add context to these problems. Rather than simply having the algebra tiles as a starting point, I’d like to start with an actual problem and possibly a picture. From here, students can then model with algebra tiles and follow through with some of the same activities. With some planning and a little bit of work, I think I can possibly eliminate this lesson completely and embed the learning throughout the other lessons.
How are you changing a boring lesson to something more enjoyable for you and the students? Tell us about it below!
WANT TO LEARN HOW TO TEACH THROUGH TASK?

Share With Your Learning Community:

About Kyle Pearce
I’m Kyle Pearce and I am a former high school math teacher. I’m now the K-12 Mathematics Consultant with the Greater Essex County District School Board, where I uncover creative ways to spark curiosity and fuel sense making in mathematics. Read more.
Read More From The Blog