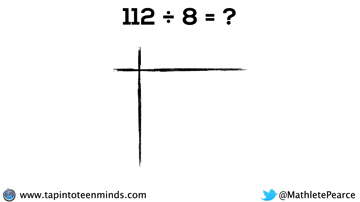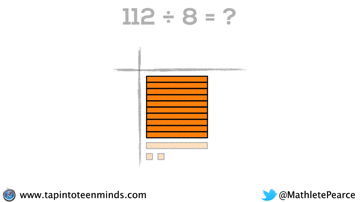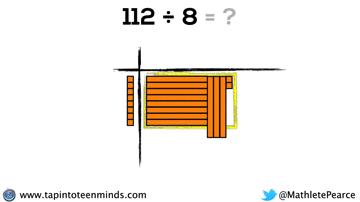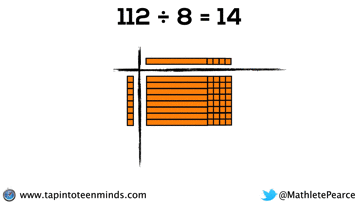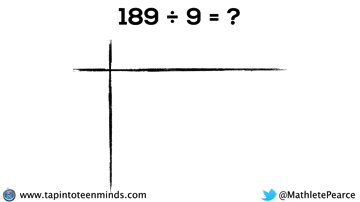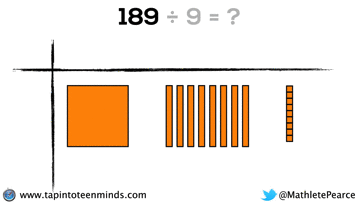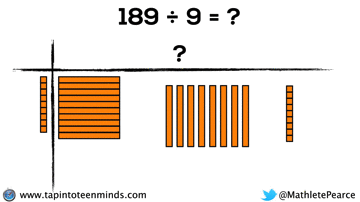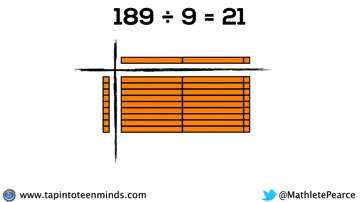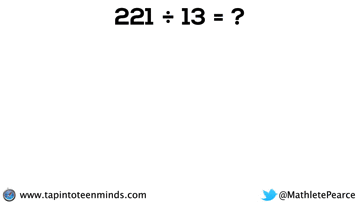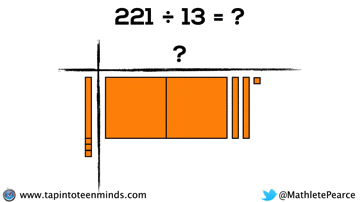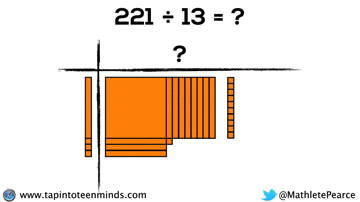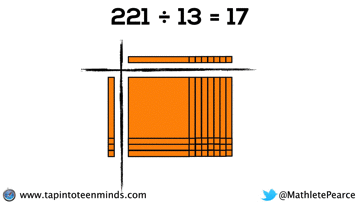HSD Math Professional Development Workshop

May 2017

FEEDBACK FORM

Thanks for inviting me to learn with you at the Hanover School Division (HSD) for a day full of math professional development!

THIS PAGE WILL BE UPDATED AFTER THE SESSION TO REFLECT MORE ACCURATELY WHAT WAS EXPLORED

Here’s a summary of what we explored today. Looking forward to connecting again soon!

---

After a brief presentation about avoiding the rush to the algorithm, we took some time to explore a 3 act math task with a very low-floor and high-ceiling, called the Airplane Problem:

[threeactshortcode the_query=”post_type=realworldmath&p=18652″]

In the airplane problem, we made predictions and made connections to multiplication and the order of operations by writing expressions. There are extensions to this task that we did not explore today, but are applicable for grade 9 applied.

---

Counting Principles

We briefly discussed the importance of counting and quantity principles, but focused on the importance of unitizing. A full summary is below:

[postshortcode the_query=”p=18603″]

---

Would You Rather?

After break, I shared Would You Rather?, a website created by John Stevens that provides all kinds of great warm-up problems for a range of grade levels including grade 9 applied:

Here’s a visual animation of the second problem we did involving fractions:

Check out https://t.co/d8dzE1b7BR by @Jstevens009.

This problem inspired me to animate a visual solution. #GECDSB #MTBoS #RMSOntario pic.twitter.com/4LmdILbTzk

— Kyle Pearce (@MathletePearce) April 28, 2017

---

Exploring the Progression of Multiplication

We made a leap from counting principles and unitizing to multiplication and specifically, using arrays and area models.

[postshortcode the_query=”p=17501″]

As an aside, you might consider looking at the “Japanese Multiplication” or “Stick Multiplication” which is derived from base ten block representation:

[postshortcode the_query=”p=18762″]

---

3 Act Math Task: Donut Delight

After lunch, we explored the Donut Delight 3 act math task where we played with multiplication to predict how many donuts there were in the “double hundred dozen” box and then used repeated subtraction to lead to a flexible division algorithm for division when we tried to find how many layers there were.

[threeactshortcode the_query=”post_type=realworldmath&p=18719″]

---

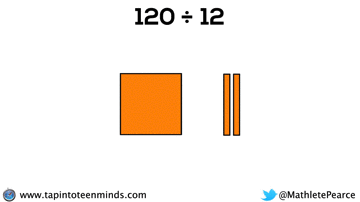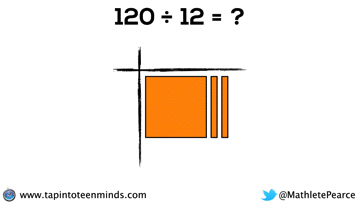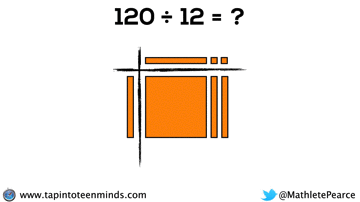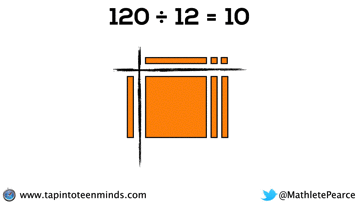
Progression of Division

We didn’t have time to dive into division with base ten blocks, but I thought I’d put that here for you to reference:

---

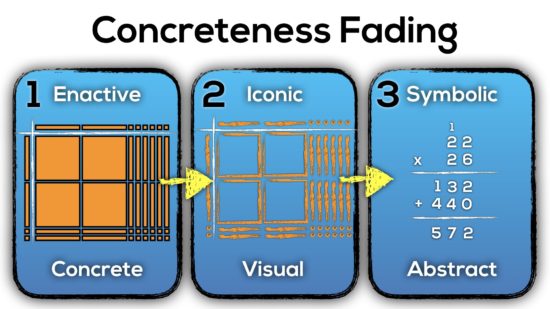
Concreteness Fading

We attempted to summarize the use of manipulatives on a continuum called “Concreteness Fading”. While the name suggests that concrete manipulatives fade away over time, it is important to remember that they fade away with one layer of abstraction and then reappear as a new layer is “piled” on.

Here are some other tasks we explored as well:

[threeactshortcode the_query=”post_type=realworldmath&p=13552″]

[threeactshortcode the_query=”post_type=realworldmath&p=13681″]

[threeactshortcode the_query=”post_type=realworldmath&p=13730″]

The Stacking Paper Tasks are also available on iOS as a multi-touch book for iBooks:

Grab It!

Learn more about what’s inside the multi-touch book here.

Or, consider accessing these tasks in an interactive way via Google Sites.

3 Act Math Tasks: Curious Math iTunes U Course

Access over 30 tasks with all resources downloaded directly to your iOS Device to avoid streaming media in your classroom through the Curious Math iTunes U Course:

Enrol in Course

<

h2>Feedback Appreciated!

<

h2>

Hope you folks found this YCDSB math professional development experience useful.

I’d be delighted to come back and learn alongside you all again sometime soon!