How Simple Scenarios Lead to Complex Math

Just a few hours ago, I was mentioned in a Tweet by @i2Learn with a link to a picture of how math is all around us:

At first glance, the photo looks like a great opportunity for introducing the basic concept of arrays and multiplication. However, since I have been using algebra tiles quite extensively this semester, the photo immediately reminded me of how I used similar photos for introducing distributive property.

Special thanks to @MathMinds for sharing the photo and @i2Learn for drawing my attention by mentioning me in the Tweet!

Simple Use of Arrays / Multiplication

In the above image, I’ve outlined what most would probably see when looking at this photograph: a basic 4 by 6 multiplication problem where

$latex 4 \times 6 = 24 $

Nothing too crazy going on here, right? Let’s look at how we can help younger students break down multiplication problems into smaller, possibly more manageable calculations:

Breaking Down Multiplication Into Manageable Chunks

Although many students that have an understanding of multiplication by grouping may not find 4 times 6 difficult, expanding simple multiplication tasks into a series of smaller multiplication problems can be beneficial as two-, three-, and four-digit multiplication is introduced.

In this case, rather than simply writing 4 x 6 = 24 apples, we see:

$latex 4 \times 4 + 2 \times 4
= 16 + 8
= 24 $

In a primary classroom, a possible question could be:

Show how many different ways you can split the apples up using addition and/or multiplication.

Implicitly Using Common Factoring

Patterning is something that is introduced early in Ontario math classrooms, but I feel that we miss key opportunities to begin using some of the tools students will learn later; in this case, much later. While multiplication is typically introduced as a certain number of groups containing a certain number of items, we can extend this to look for groups of products.

Since we see in the photo that there are three groups of 4 by 2, we can begin implicitly introducing the concept of common factoring. In the image above, 2 is a factor of 6, thus yielding 3 groups of 2.

$latex 4 \times 2 + 4 \times 2 + 4 \times 2 $
$latex = 3 \times (4 \times 2) $
$latex = 3(4 \times 2) $
$latex = 3(8) $
$latex = 24 $

Break it down even further to get:

$latex 2 \times 2 + 2 \times 2 + 2 \times 2 + 2 \times 2 + 2 \times 2 + 2 \times 2 $
$latex = 6 \times (2 \times 2) $
$latex = 6(2 \times 2) $
$latex = 6(4) $
$latex = 24 $

Pretty basic stuff, but I will definitely be using this as an example when I formally introduce common and other types of factoring in my grade 10 course and beyond.

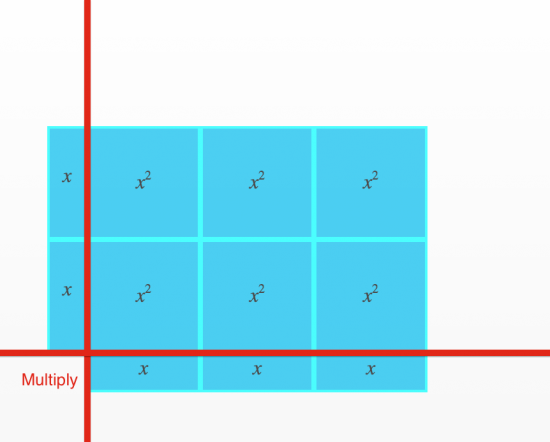
Increasing Complexity of a Simple Problem by Introducing Algebra

In math education, I think we skim over the basics to maximize the amount of time we can spend on more complex concepts. In many cases, students do not have the foundation necessary to move on to more abstract concepts. A common belief amongst us math teachers is that students do not know their math facts like memorizing the times tables. While it might seem that students who know their 10×10 or 12×12 times tables are stronger and thus math facts are the urgent student need, I think it is much deeper than that. I believe that most of these students who can multiply off the cuff have a deeper conceptual understanding of what it means to multiply. For all we know, students might just have multiplication up to 6 memorized and derive the rest on the fly; we’d never know the difference. A student who can’t multiply 4 x 6 probably doesn’t have the conceptual understanding that they can break the problem down into 2 groups of 2 x 6, 2 groups of 4 x 3, or 3 groups of 4 x 2.

The same can be said as we begin introducing algebra to our students. Remember, understand how to get there the long way before taking shortcuts. I’m not confident that many of my students coming into grade 9 could take this simple photo of 24 apples and break it down as we have done in the above examples. However, this basic problem can be a huge help as we begin introducing problem solving with algebra moving forward.

In the image above, you can quickly see that introducing a variable has immediate context for the students. Relatively quickly, students will be able to determine that x = 2 in this case. Yes, I know; some students may ask “why are we using a variable if we know what the number is.” In this case, I think that the magic of math can win them over.

By simply replacing “2” with “x” from the previous example, we get the following expression which can then be simplified:

$latex x \times x + x \times x + x \times x + x \times x + x \times x + x \times x $
$latex = 6 \times (x \times x) $
$latex = 6(x \times x) $
$latex = 6(x^2) $
$latex = 6x^2 $

Taking your simplified expression and substituting a value for x when x = 2, students can quickly see:

$latex 6x^2 $
$latex = 6(2^2) $
$latex = 6(4) $
$latex = 24 $

Beauty!

Simplifying Prior to Multiplying

What better way to justify why we are bringing algebra into the picture than to highlight how many steps we can save by doing a little bit of the thinking (and work) upfront:

$latex 2x \times 3x $
$latex = (2x)(3x) $
$latex = 6x^2 $

Don’t forget that we can also take this real world problem and represent with algebra tiles:

Resource in PDF Form

Feel free to grab the images and expressions from this post in PDF Format here or by clicking the image below:

I know that this post sent me off on a bit of a tangent, but I thought it was worth sharing. Do you have any ideas to help teachers make connections from primary through junior/intermediate grades? Would love to hear them in the comments!

Read More From The Blog

---

Not What You're Looking For?

Search By Criteria: