GECDSB Professional Learning Community (PLC) Sessions
Thanks for inviting me to learn with you over the past few professional learning community days! This group is always energetic and excited to learn about meaningful manipulative use, making mathematics visual and concreteness fading!
You can scroll down to see our past sessions, or consider jumping to the specific session you’re looking for:
- Tuesday December 6th, 2016
- Friday February 24th, 2017
- Wednesday March 1st, 2017
- Friday March 10th, 2017
- Friday February 24th, 2017
- Tuesday March 21st, 2017
Tuesday December 6th, 2016
Here’s a summary of what we explored today:
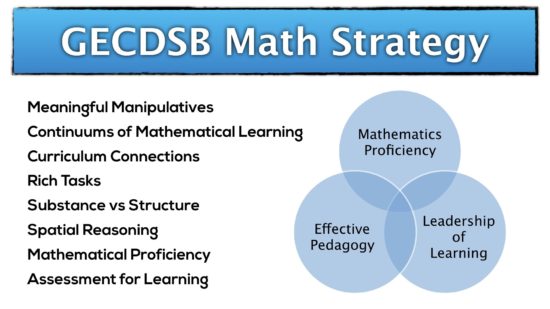
The GECDSB Mathematics Strategy
Mathematical Proficiencies
The full GECDSB Mathematics Vision is here.
Pedagogical System
Based on work by Glenda Anthony and Margaret Walshaw, the Pedagogical System is the result of a meta-analysis of many studies which are summarized into four key components:
You can also see a “silent solution” animation of the pedagogical system in detail:
Tools and Representations
We discussed the importance of tools and representations to help students see mathematics from different perspectives. These quotes help us better understand some of the other important reasons tools and representations are so important:
Marian Small gives her perspective on representations in math class:
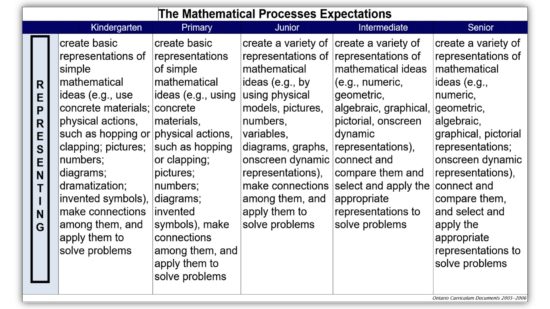
K-12 Process Expectations: Representing
We very briefly discussed the 7 Process Expectations in mathematics that are embedded throughout our K-12 Mathematics Curriculum and looked in particular at the expectations for Representing:
Task: The Sandwich Problem
With manipulatives on the table (square tiles, relational rods, cubes, pattern blocks and fake money) we attempted to find concrete and/or visual representations that could help us solve and justify the following task:
Original task was shared at a Ministry SIM Session. Here’s the slide deck.
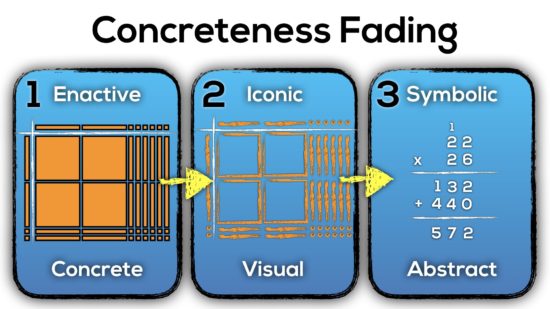
Concreteness Fading
We attempted to summarize the use of manipulatives on a continuum called “Concreteness Fading”. While the name suggests that concrete manipulatives fade away over time, it is important to remember that they fade away with one layer of abstraction and then reappear as a new layer is “piled” on.
Friday February 24th, 2017
Today, we explored the progression of division including partative and quotative division, using manipulatives to divide numbers including square tiles and base ten blocks when the numbers are two digit or greater.
I am still working on a post that will have all of these visuals and problems included in them, so hang tight or check back soon.
Wednesday March 1st, 2017
Here’s a summary of what we explored today:
Extending to Multiplication and Division
After spending some time doing some more division with base ten blocks and arrays / area models, we explored the Donut Delight 3 act math task where we played with multiplication to predict how many donuts there were in the “double hundred dozen” box and then used repeated subtraction to lead to a flexible division algorithm for division when we tried to find how many layers there were.
[threeactshortcode the_query=”post_type=realworldmath&p=18719″]
While we didn’t explore the progression of multiplication explicitly, the following post might be useful to extend some of the thinking from the donut delight task.
[postshortcode the_query=”p=17501″]
Friday March 10th, 2017
Today, we had an opportunity to begin looking at Fraction Constructs based on the work from the Paying Attention to Fractions document.
[postshortcode the_query=”p=17492″]
Tuesday March 21st, 2017
Today, we continued our work with Fraction Constructs (Part-to-Part, Fraction as Quotient, and Fraction as Operator).
To access the fraction visuals and a full detailed post about the Progression of Fractions, click here.
While we didn’t get to multiplication of division of fractions, here is a pretty cool task that would be easily modifiable for a grade 4 and 5 classroom looking to play with more contextual situations with fractions:
[threeactshortcode the_query=”post_type=realworldmath&p=16696″]
Looks like the next time we meet as a group will be at the Southwood Staff meeting on April 12th where we plan to do more Exploring Fractions as a staff, look at number lines with fractions and other numbers, and how one might monitor progress in the classroom.
Hope you folks found this professional learning experience useful.
I’d be delighted to come back and learn alongside you all again sometime soon!