Exploring Fraction Constructs and Proportional Reasoning
Fractions are a beast of a concept that causes struggles for many adults and students alike. While we all come to school with some intuition to help us with thinking fractionally and proportionally, the complexity quickly begins to increase as we move from concrete, to visual, to symbolic and from identifying, to comparing, to manipulating. Fractions are formally introduced in the Ontario Math Curriculum when students begin dividing whole objects into pieces and identify these pieces using fractional names (e.g.: halves; fourths or quarters) and continues to promote the development fractional fluency concretely through each grade. Interestingly enough, it is often said that students struggle much more with numbers represented in fraction notation than those represented in decimal notation, yet the word “fraction” appears in the curriculum document 99 times beginning in grade 1, while the word “decimal” appears only 69 times beginning three years later in the 4th grade. While it might be true that fractions tend to intimidate, I wonder if our dependence on the calculator has tricked us into believing we are more fluent with quantities represented in decimal form than is reality.
Paying Attention to Fractions
As I did with the Progression of Proportional Reasoning, I’d like to reference the Paying Attention To Mathematics series released by the Ontario Ministry of Education Literacy and Numeracy Secretariat (LNS) called Paying Attention to Fractions. These guides are a great start to help you wrap your head around big ideas in mathematics and thus, this post will attempt to expand on the ideas shared in this particular document.
Why Fractions?
As if the struggles our students experience when working with fractions aren’t enough justification, I like this quote shared in the guide:
“No area of elementary school mathematics is as mathematically rich, cognitively complicated, and difficult to teach as fractions, ratios, and proportionality. These ideas all express mathematical relationships: fractions and ratios are ‘relational’ numbers. They are the first place in which students encounter numerals like ‘ 3/4 ’ that represent relationships between two discrete or continuous quantities, rather than a single discrete (‘three apples’) or continuous quantity (‘4 inches of rope’).”
(Litwiller & Bright, 2002, p. 3)
What Is A Fraction?
A fraction is a number.
While many think of fractions and fractional notation as a means to represent quantities that are not whole, all quantities can be represented as a fraction.

While these descriptions are simple on the surface, they do not appropriately communicate the complexity throughout the progression of fractions and the many big ideas connected to this progression.
Connecting Proportional Reasoning and Fractions
If you recall from my last post, proportional reasoning takes place when one compares two quantities in relative terms rather than absolute terms. Thus, it can be said that a fraction provides a means for representing that relationship between two numbers. However, it is important not to confuse that while the numerator and denominator can be thought of as two quantities that are related, a fraction is a single quantity that can be represented on a number line.

So where does the progression of fractions begin?
As it turns out, pretty early on!
Young learners begin their journey through the progression of fractions in tandem with the progression of proportional reasoning as they make comparisons between two (or more) quantities such as:
- this bag is heavier than that one;
- I’m “this much” shorter than you are; and,
- there are 5 more red candies than green.
While these early comparisons are likely absolute (i.e.: additive) in nature, we are one step closer to comparing these quantities relatively (i.e.: multiplicatively). This multiplicative comparison between two or more quantities is called a ratio.
In these early stages of the progression of fractions, young learners often begin thinking fractionally as they explore geometric quantities like volume and area; comparing a part relative to its whole.
Counting Cartons: Part-Whole Relationships
Since the progression of fractions begins for most by thinking of a part relative to a whole as a means to measure as well as the lack of conceptual clarity related to fractions and proportional reasoning, it should be no surprise that many think of fractions narrowly as a part-whole relationship alone.
Let’s start our exploration of fraction constructs beginning with the most common part-whole fraction.
Have a look at the image below:

I might ask students:
How many eggs are there?
How many different ways can you represent that quantity?
While the question is clearly asking students to determine the quantity of eggs, asking students to share how many different ways they can represent the quantity encourages students to potentially think beyond counting relative to 1 egg. While we can expect that many students will be able to communicate that there are 18 eggs, others may get creative and unitize (i.e.: 3 groups of 6; 9 groups of 2; etc.) or even reference the number of eggs relative to egg cartons. By asking students to represent the quantity in different ways, we are promoting proportional reasoning by changing the whole that the quantity of eggs is being related to.
After students share out with a partner, I might ask students more specifically:
How many cartons of eggs are there?
This prompt maintains the same “part” (18 eggs), but changes the whole (1 carton rather than 1 egg).
After students have some time to think independently, I would have them share out with their table groups. Some interesting responses are sure to come up such as:
- 18/2
- 18/1.5
- 3/2
- 1.5
- 2
You may notice that by asking students to state how many cartons of eggs there are, there is room for interpretation. Some students might simply state that there are two egg cartons without considering the number of eggs present, some might give a quantity relative to two egg cartons, while others might state the number of eggs relative to a single carton.
After students have been given an opportunity to defend their thinking, I might ask students:
How many cartons are full of eggs?
This fraction construct would be an example of a part-whole relationship. Students might consider how many whole and partial cartons there are in the form of a mixed fraction (1 and 1/2), improper fraction (3/2) or in decimal form (1.5). Some common representations for these different fractional forms might be using a set model, area model or number line. The following animated gif shows each of these representations, sometimes more than one simultaneously:

You might have noticed the double-number line included in the animated gif. This idea can be very useful when making the jump from thinking fractionally to proportional reasoning.
Doritos Roulette: Part-Part Relationships
Note: This section was updated on February 27th, 2021 to better communicate my current and more clarified understanding of fractions and proportional relationships that I continue to develop.
In the Doritos Roulette 3 Act Math Task, students are asked questions that stem from the relationship of “hot” chips to “not hot” chips based on the image on the front of the bag:

I might ask students to consider the image above and ask them this question:
What ratio of hot chips to not hot chips are there in a bag of Doritos Roulette?
and,
Can I represent this ratio as a fraction?
This string of questioning is helpful for emerging some of the muddiness that exists when it comes to understanding fractions and proportional relationships.
Despite the explicit request for a part-part relationship between “hot” chips (1) and “not hot” chips (6), we often see and/or hear many share the relationship between “hot” chips (1) and the whole (7).
When asking a group of students or educators to discuss with their neighbours about whether a part-part ratio relationship can be represented a fraction or not. Great (and sometimes heated) discussions can arise from this question, which makes this exciting to facilitate.
Based on the explanation given in the Paying Attention to Fractions document referenced earlier, I used to believe that a ratio is a fraction. However, after much learning and finally coming across the work of John Van De Walle et al and their book Elementary and Middle School Mathematics: Teaching Developmentally, I now realize that while a ratio can be represented using a fraction bar, it is not a fraction.

It is worth noting that while a part-part ratio can be represented using the fraction bar, note that this construct is representing two separate quantities where the fraction bar is used as an operator to divide.
In other words, when we see fraction notation used to represent this part-part ratio as 1/6, what this is representing is:
1 hot chip ÷ 6 not hot chips
Partitively dividing these two quantities in ratio will reveal a rate:
1 hot chip per not hot chip
The rate above represents a single quantity with a compound unit of hot chips per not hot chips.
Fun stuff, right?
I know!
All of this thinking is what fuelled me to create a full self-paced online proportional relationships course to help unpack the roadmap of proportional reasoning from spatial comparison all the way to proportional relationships.
After exploring part-whole fraction construct and representing a part-part ratio using the fraction bar for the purpose of dividing, you may begin to notice how important clarity around what a given fraction represents prior to attempting any comparison or manipulation of that fraction.
While the use of a set model and area model remain fairly similar regardless of whether you are dealing with a part-whole or part-part relationship, the use of a number line changes significantly.
Recall how the number line used in the part-whole counting cartons example made identifying the part and the whole fairly intuitive:

When we attempt to use a number line with a part-part ratio relationship, you’ll notice that we cannot locate a single value on the number line because a part-part relationship is two separate quantities representing two different places along the number line:

Although the number line representation might not be as intuitive in the part-part case, you can visualize both parts and their sum represents the whole:
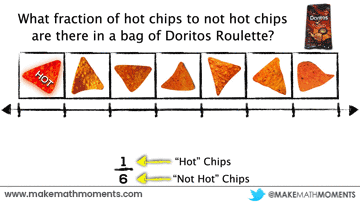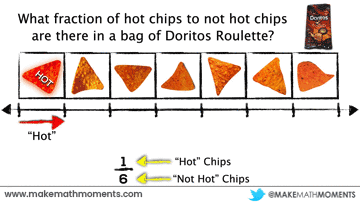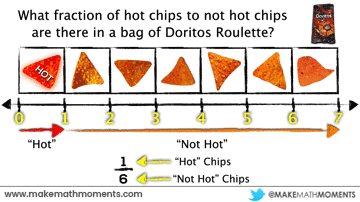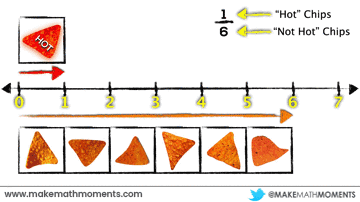
Extending from a single number line to a double-number line can help the learner see the part-part ratio relationship and easily scale both quantities in tandem. At any point along the double number line (or later, the ratio table) you can use partitive division to divide the parts to reveal a rate:
1/6 hot chips per not hot chip
or
6 not hot chips per hot chip
In this case, there are one-sixth as many “hot” chips as there are “not hot” chips. Alternatively, there are 6 times as many “not hot” chips as there are “hot” chips.
Baking Brownies: Fraction as Quotient
As mentioned above, a part-part ratio relationship can be represented with a fraction bar when the intention is for two separate quantities to be divided. In other words, when we are using fraction as a quotient. The Paying Attention to Fractions document uses an example of kids fair sharing some brownies, so we’ll stick to that and add some visuals to help.
Suppose there are 6 brownies that are to be shared amongst 4 friends fairly. How much should each person receive?

Like many situations in life, there are multiple ways to share these brownies fairly. Let’s represent a few of these methods.
Using Partitive Division to Partition the Brownies into Fourths
Since there are 4 people to share the 6 brownies, we can divide the 6 brownies into fourths and then pass them out, one-by-one:

After splitting the brownies into quarters, you’ll notice that each of the four people should receive 6 quarters. Hence why we can represent this fraction as quotient as the improper fraction, 6/4.
Sharing Full Brownies Equally, Then Partitioning Remainder
Some people might find it useful to share whole brownies equally and then when there are not enough whole brownies to share fairly, consider partitioning up the remaining brownies appropriately:

Partition Brownies Into Four Equal Portions
This method involves considering all 6 brownies and where cuts must be made to create four equal groupings:

For each of the methods above, we could also consider the use of a number line to support the partitioning of the brownies to distribute a fair amount to each person. Here are a few examples:
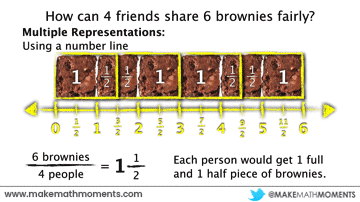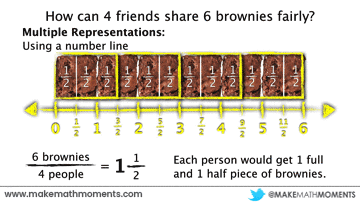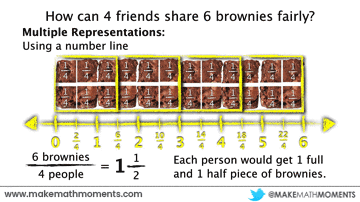
Fraction as Operator
Another common construct is using a fraction as operator where a fraction is used to act as a function to:
- scale a quantity larger;
- scale a quantity smaller; or,
- find equivalent fractional quantities.
Using a fraction as operator to scale a quantity larger or smaller feels pretty intuitive.
Consider a $100 investment.
Over time, this investment could increase in value or decrease in value.
If the investment decreases to $50, we could say that the investment “halved” from its initial value of $100.
In other words:
1/2 of $100 = $50
It is also possible that the $100 investment increases in value to $150.
In that case, we could say:
3/2 of $100 = $150
In both of the above cases, the fraction is still a part-whole relationship, however the intent is to use the fraction for scaling.
While it seems natural in both cases to think of the operation as simply multiplication, we can approach both cases through multiplication and/or division.
For example, in the second case, we could arrive at the equivalent result of $150 through each of these approaches:
3/2 of $100
$100 multiply by 3, divide by 2
$100 divide by 2, multiply by 3
Thus, the intent of the fraction 3/2 was to use as a function for operating.
Exploring Fractions Developmentally
Now that we have an understanding of the different fraction constructs and when we might bump into those situations, many are likely wondering how students will develop their understanding of fractions.
As mentioned earlier, students will likely bump into fractions through experiences in the world around them. For example, seeing that half of a brownie tray is missing, one fourth of a glass of milk remains, or each of three children will receive one third of the share of chocolates.
Exploring part-whole fractions beginning with unit fractions through counting can be helpful for building an understanding of the relationship of the part to the whole. This can be done through mathematical modelling using area models such as a bar model to encourage representing, comparing and ordering of fractions.
How Many Rolos: Adding and Subtracting Fractions

Let’s have a look at another problem. We mind as well keep the context as food, because that is just yummy.
There are 7 pieces in every full roll of Rolo chocolate.
Two partially eaten rolls are found in a drawer; one with 5 pieces and the other with 4 pieces.
How many full rolls of Rolo are there?
If we use concrete manipulatives or visuals, like we will in this instance, it is much easier to see how to add and subtract fractions. In this case, we’ll show a few different representations including how using a number line can be helpful:

So in this particular example, you can see that 5 pieces plus 4 pieces will yield 9 pieces, which is more than a full 7 piece roll; 9/7 or 1 and 2/7.
Gimme a Break: From Adding and Subtracting to Multiplying Fractions
If you’re a 3 act math fan, you might be familiar with my Gimme a Break 3 act math task involving the use of fractions as operators. I should note that while there are some useful pieces in that task, it has really evolved over time and I just haven’t had the time to update the post yet. Here’s some of the pieces I’ve added along the way.
The task begins with an opportunity for students to notice/wonder after watching a video of me opening a KitKat bar.
Later in the task, the following video is shown asking students to consider what operation could be taking place:
Since the video is open ended, I’m always hoping that all students will be able to share something mathematical about the situation. For example, we might see some responses like these:




While I find that multiplication of fractions seems to be the one operator I hear the least noise about, my gut tells me that it is more about being able to remember the algorithm and not due to any conceptual understanding. In my experience, many students can manage to remember to “multiply the tops, multiply the bottoms” without necessarily having any real conceptual understanding to fall back on in times of doubt.
Dividing Whole Numbers by Fractions and Fractions by Fractions
On the other hand, division of fractions seems to be a sore spots for many students (and adults) because the algorithm is a bit more complicated and less intuitive. Pair that with a very low level of conceptual understanding as to why the algorithm actually works and you’ll end up with confusion and frustration for many. The gap between the pure memorization of steps and the conceptual understanding of what dividing fractions really means is often so large that many educators simply follow suit and focus purely on the algorithm. While I believe it is so important to build the conceptual understanding behind a complex idea like dividing fractions, I know that the task can be quite difficult and many teachers aren’t so sure how to approach it. When we rush to an algorithm before constructing conceptual understanding, students (and adults) are often very difficult to engage in the heavy thinking required to connect the dots. This leaves many teachers believing that successful use of the algorithm is enough (or all they have time for) and they just move on to the next topic.
Let’s look at the Gimme a Break context in terms of division of fractions. With manipulatives on the table such as pattern blocks or relational rods, I might ask students:
What would 1 ÷ 1/4 “look like” in terms of the KitKat task?
Can you show a neighbour what that looks like to you?
Hopefully students come up with some representation to model what a whole KitKat bar would look like an a quarter of a KitKat bar:
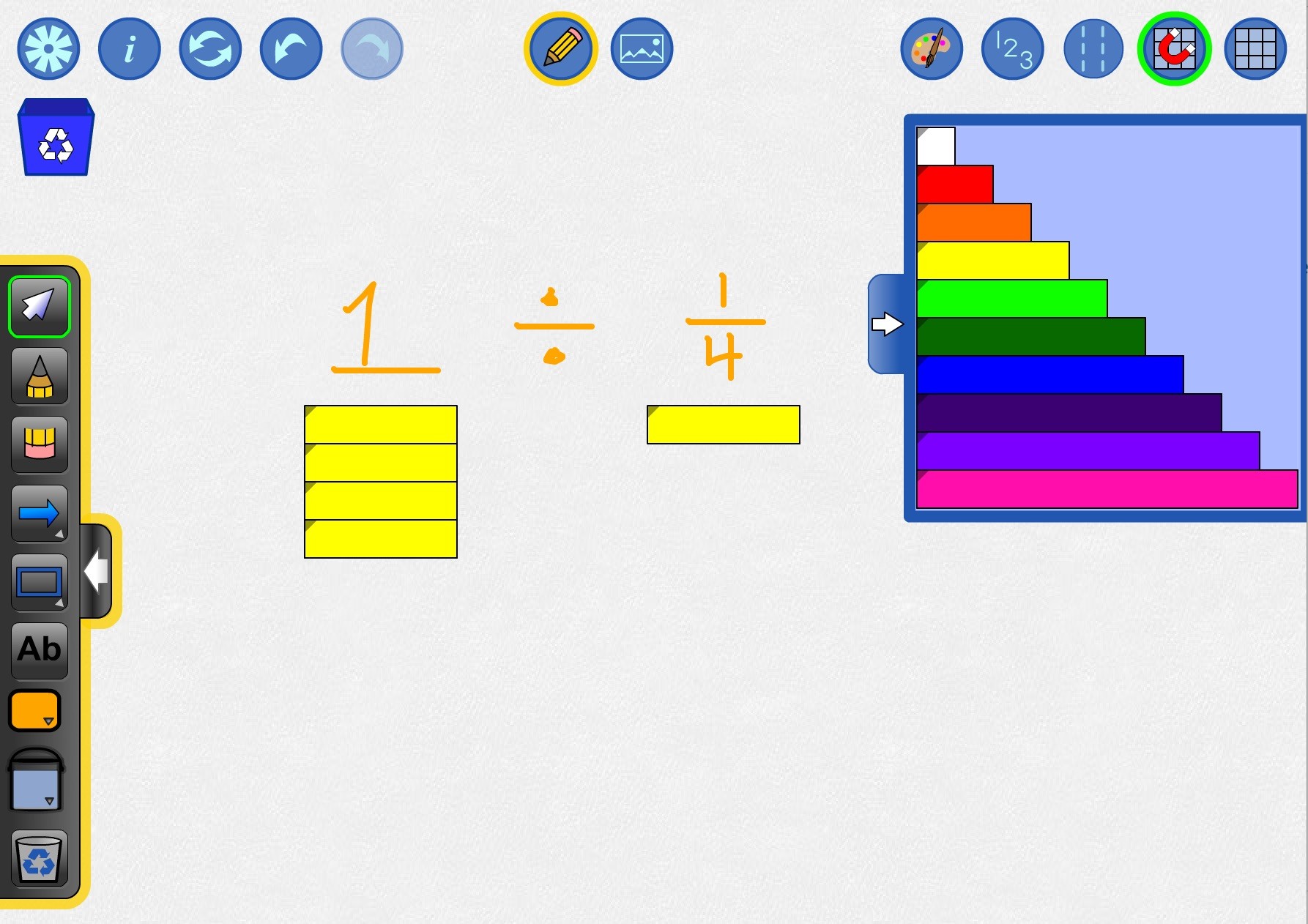
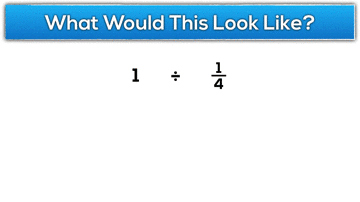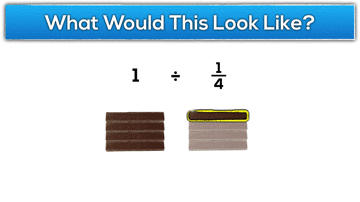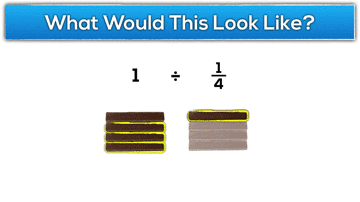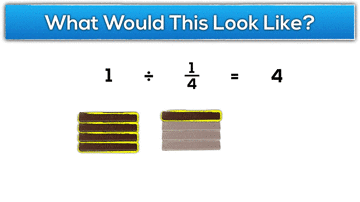
For example, 2 divided by 1/4:

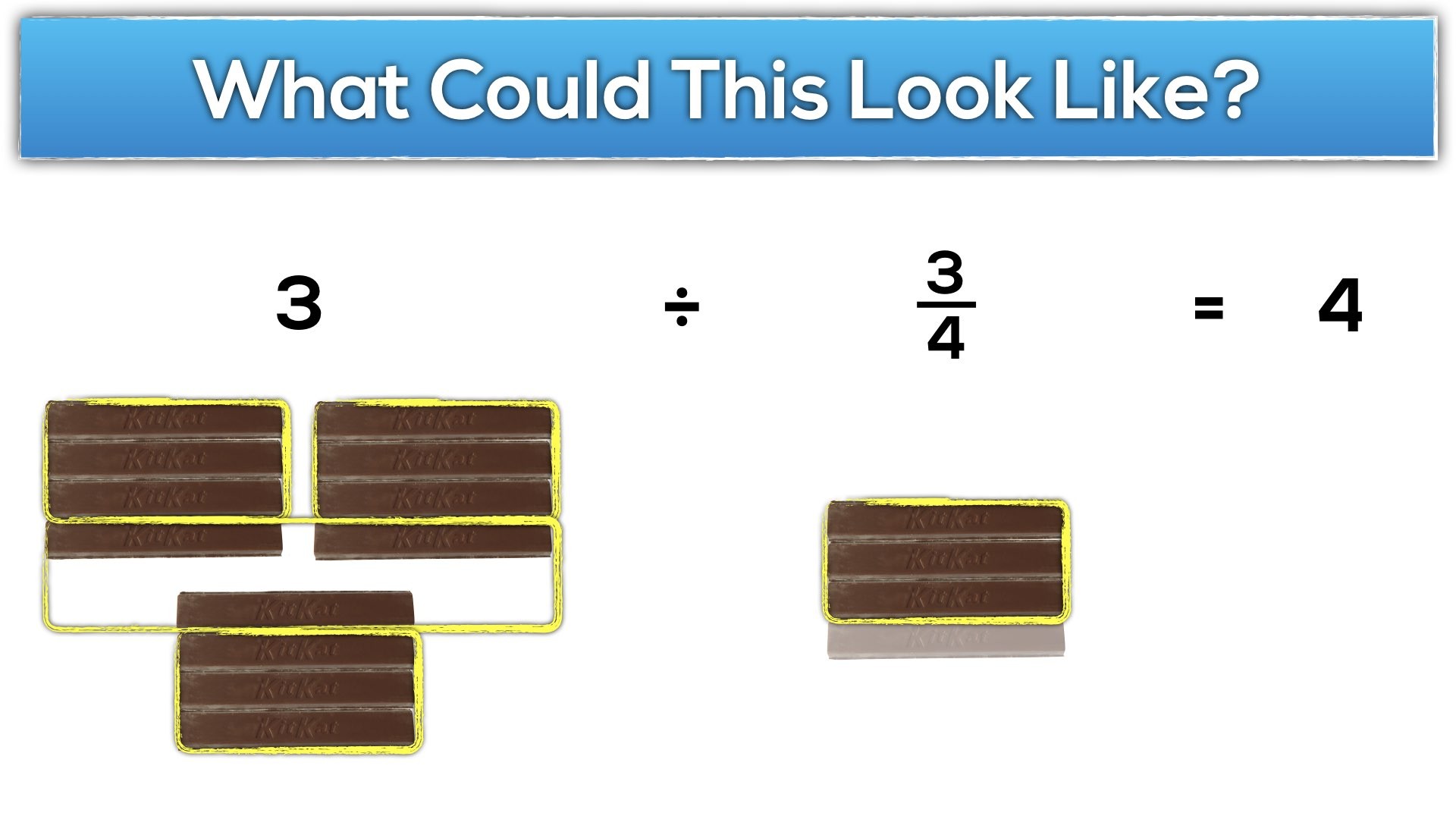

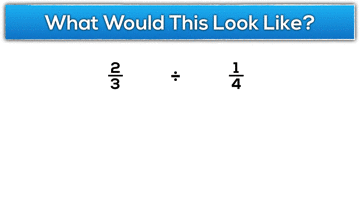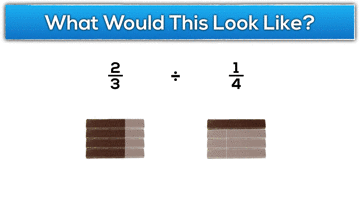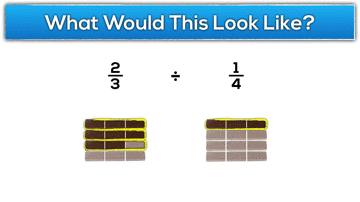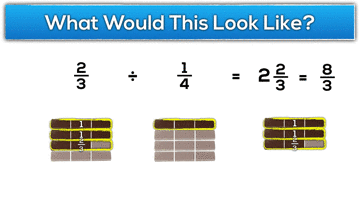

Throughout this post we have tackled the idea of fraction constructs by using a similar approach to how I introduce most big ideas in math class: using math tasks that are contextual, visual and concrete in order to build a conceptual understanding.

Let’s avoid the rush to the algorithm and slow down to let kids truly experience and understand mathematics. I’d appreciate any pieces I should add to this post in the comments section.


Thank you so much for this – great examples of how to understand and teach.
Thanks, particularly for this
“Based on the explanation given in the Paying Attention to Fractions document referenced earlier, I used to believe that a ratio is a fraction. However, after much learning and finally coming across the work of John Van De Walle et al and their book Elementary and Middle School Mathematics: Teaching Developmentally, I now realize that while a ratio can be represented using a fraction bar, it is not a fraction.”
I have always hated that assertion in “paying Attention” and in the curriculum doc. Students already find fractions confusing without considering them as part-part relationships. I have not found other math teaching resources that use this definition – much better to say that sometimes ratios are written a/b. Plus, Van de Walle has always been my favourite math professional resource!
So glad that you found that little snippet helpful! Many enjoy getting into “math debates” over what is and what is not a … (insert math term) and this is one of the many challenges we face as math educators: we aren’t even clear and concise on what we mean when we say something (like ratio, or rate, or fraction!)
Thank you for sharing your experience in the confusions you had with fractions and proportions. There is so much confusion around that concept, and it’s not clearly understood till you see a concrete visual representation of the two concepts.