If you were to use this language for the first time without ensuring students understand the meaning, they may misinterpret the meaning in a variety of ways. While this will result in a different final answer, the student thinking we are after should still be evident through their use of tools and representations to model their understanding of the mathematics.
Although the language “1 one-sixth cups of sugar” and “1 sixth cups of sugar” may seem confusing or possibly even unnecessary at first blush, approaching fractional thinking from counting (i.e.: “1 one-sixth, 2 one-sixths, 3 one-sixths, etc.”) can be very beneficial for our early fraction work as well as when we begin operating on fractions later on.
Consider the Building Understanding of the Unit Fraction article in the resources section of the Walk The Line task from the Fractions Learning Pathway on the Ontario Ministry of Education EduGains website and you’ll see some great examples of how a more intentional focus on the unit of measure can be helpful in many domains of mathematics.
What Is A Unit Of Measure?
A unit of measure helps measure quantities by determining:
How many of one thing there are in another.
The selected unit of measure is iterated (or used repeatedly) to measure a quantity relative to the selected unit.
Before we can measure a quantity, we must:
- Select a quantity to be measured.
- Select a unit that has the same attribute as the quantity you are measuring.
- Compare the units – by filling, covering, matching or using known measures. Recognize the number of units needed to equal the measurement.
If the quantity we are looking to measure is how many blue squares, we could do so by:
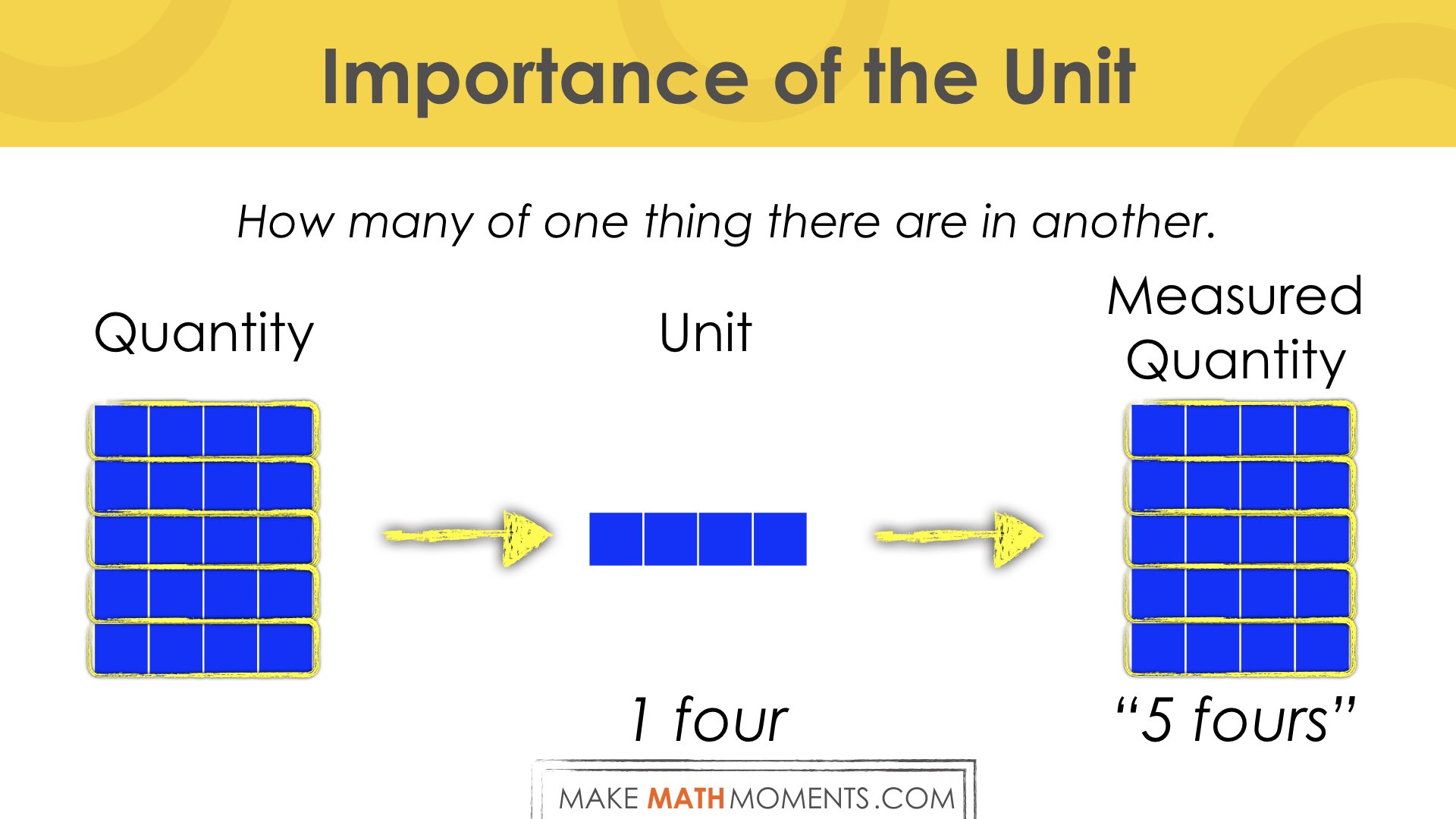
- Select a quantity to be measured: Number of Blue Squares
- Select a unit: 1 group of four or 1 four.
- Compare the units: 5 groups of four or 5 fours.
Another quantity we could measure could have the attribute of area:
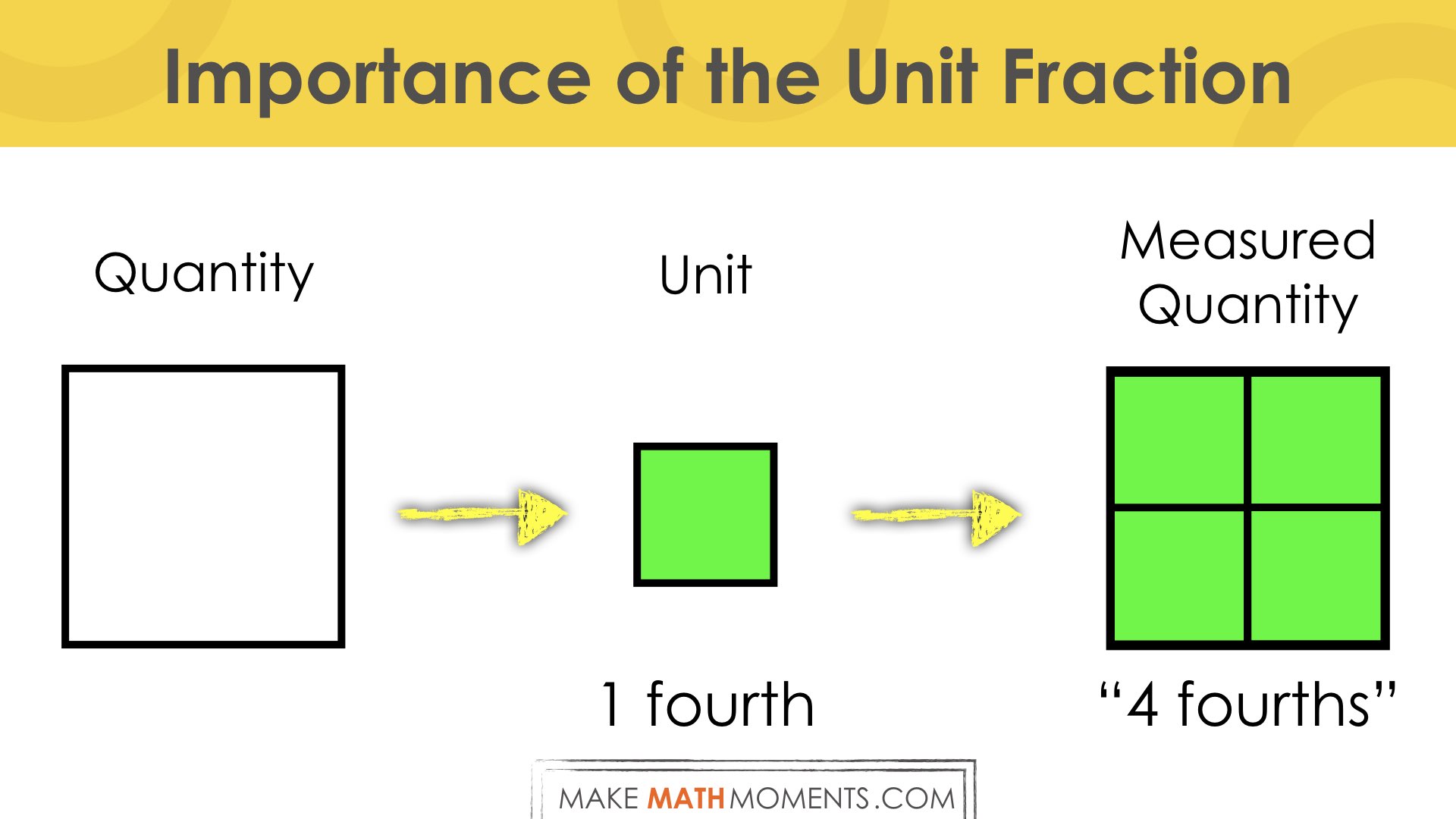
- Select a quantity to be measured: Area of square
- Select a unit: 1 one-fourth or 1 fourth.
- Compare the units: 4 groups of one-fourth or 4 fourths.
Finally, one last example of a quantity to measure might have the attribute of length:
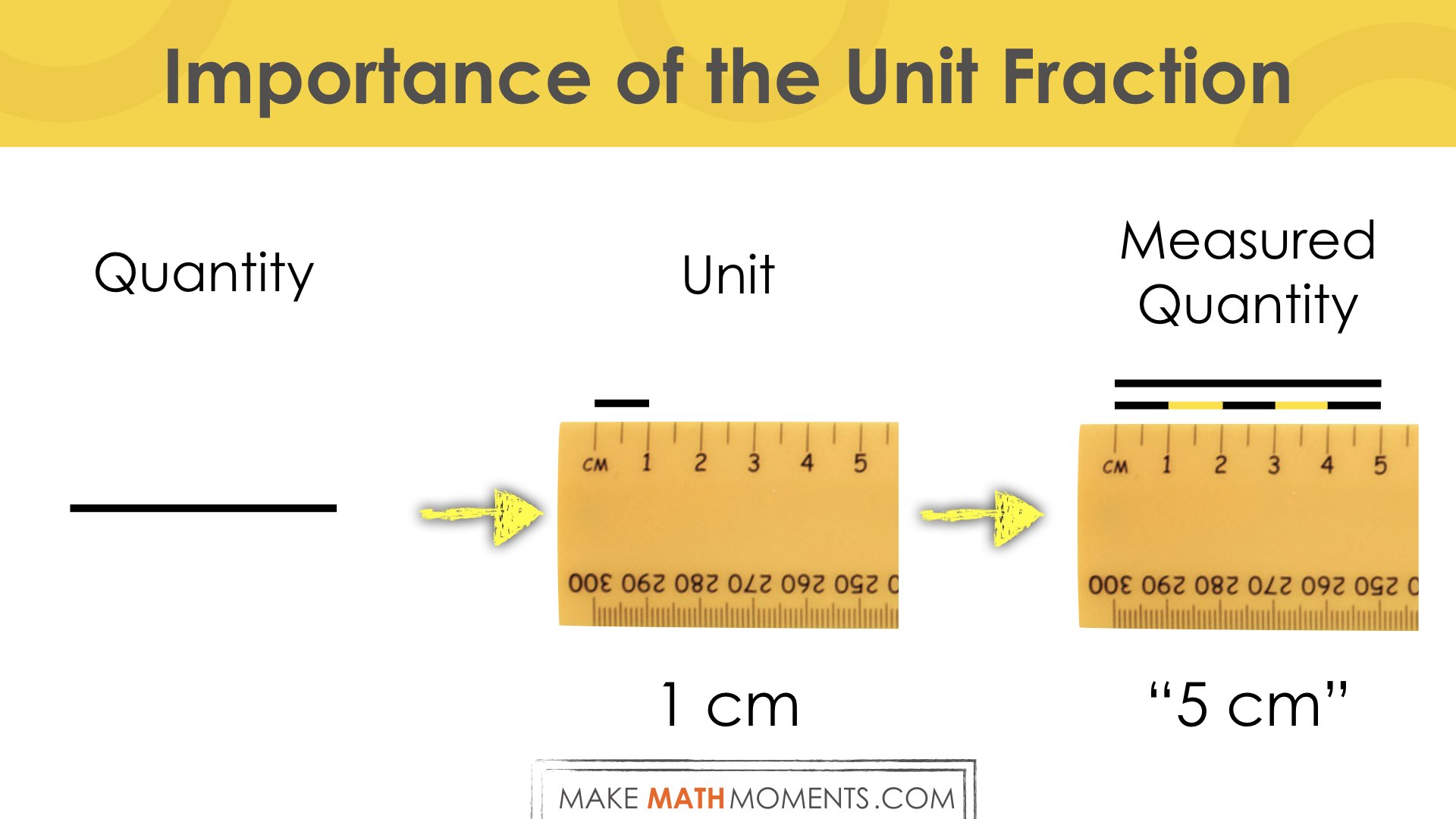
- Select a quantity to be measured: Length of the line.
- Select a unit: 1 one-centimetre or 1 cm.
- Compare the units: 5 groups of one-centimetre or 5 cm.
Focusing On The Unit Of Measure Is Simple, But Essential
Although this might seem quite straight forward and maybe even unnecessary at first blush, I think it is important for us to understand that as soon as children begin counting using one-to-one correspondence, they are counting with a unit of measure in mind. I’m fairly confident that when they are counting the number of dinosaurs that are laid out on the floor they are not explicitly aware of their use of a unit of measure. However, as they are counting that entire group of dinosaurs, a single dinosaur is the unit of measure being used to measure the quantity.
Later, children begin to skip count by 2’s, 5’s, and 10’s which extend this unit of measure to a group of 2, 5, and 10, respectively. This shift from one-to-one correspondence towards “one-to-many” correspondence – known as unitizing – leads children to begin to flirt with the idea of our base-10 place value system.

Let’s take some time to dive into how helpful explicitly focusing on the unit of measure can be when operating on a variety of mathematical concepts.
Whole Numbers
Whether we are asking students to add dinosaurs, blocks, cards, or any other quantity involving whole numbers, we often ask them to add one quantity with another without reference to the unit of measure.
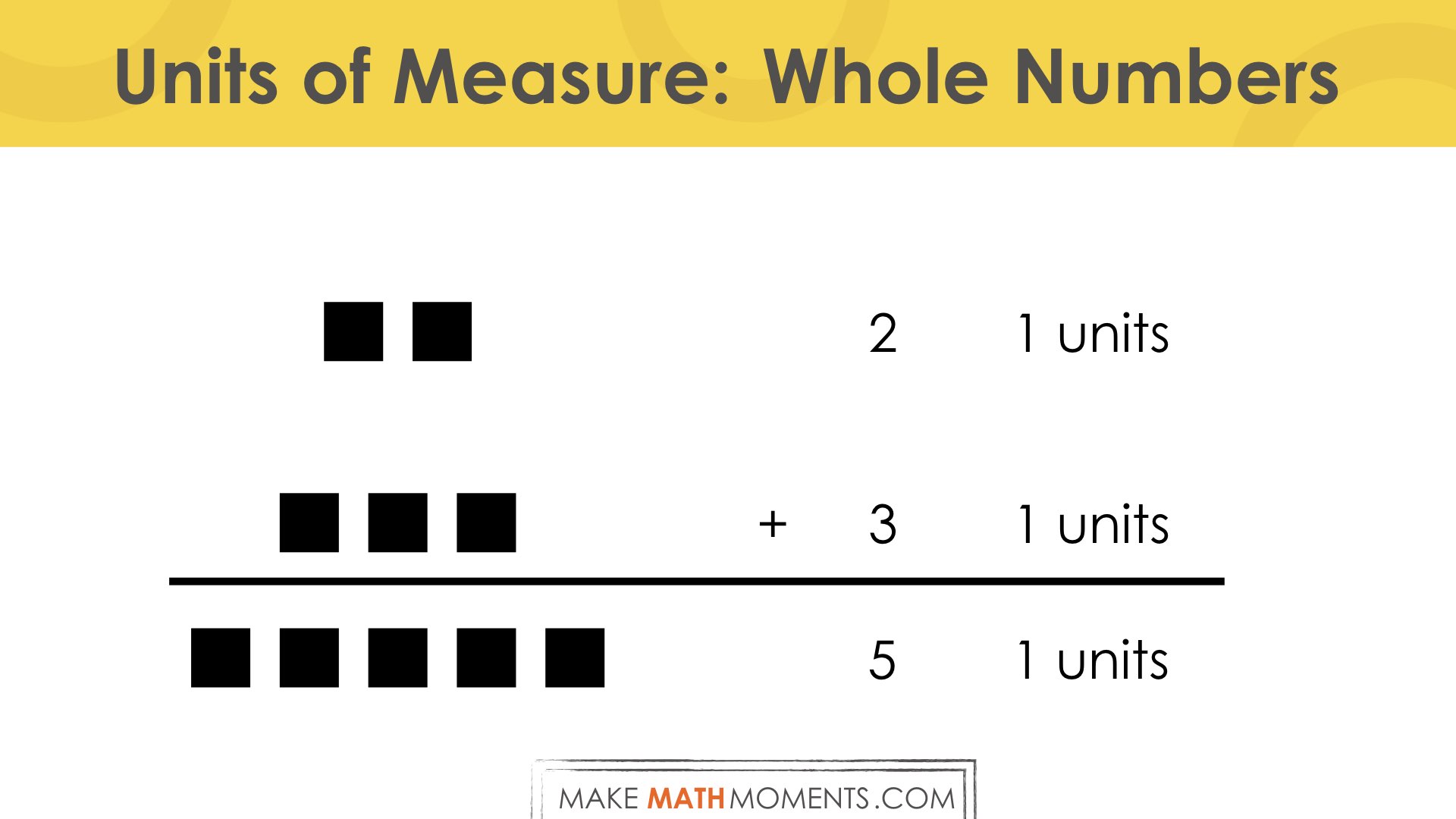
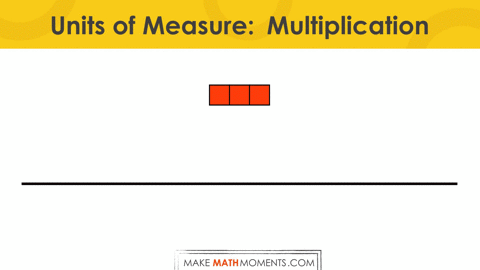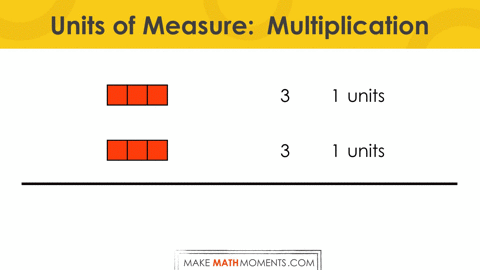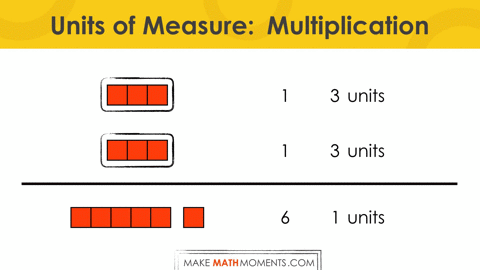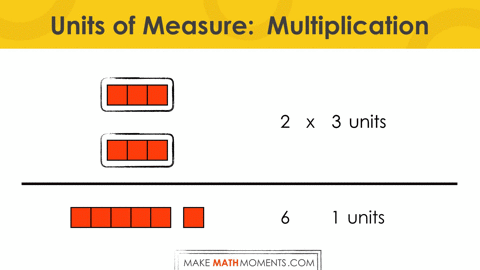
For example, whole numbers: 2 + 3 = 5
This might not seem like a big deal on the surface, however having students get in the habit of referencing the unit of measure consistently will prove to be helpful later as the mathematics they engage in becomes more complex over time.
So instead of simply adding “2 plus 3”, we can have students reference the unit of measure being used to measure the quantity.
That might be 1 dinosaur, 1 block, 1 card, or In a generic situation, we can simply say “1 unit”:
2 1 units
+ 3 1 units
================
5 1 units
Let’s continue exploring…
Large Numbers
Those of you who read my blog and my tweets know that I have a daughter and son at home. As soon as both of them were able to add whole numbers like 2 1-units and 3 1-units, I began tossing larger numbers to chew on.
Taliah (grade 1) is currently adding numbers in the billions.
Don’t believe me?
Ask her to add 2 1-billions and 3 1-billions and she’ll quickly tell you that the total is 5 1-billions.
It’s easy!
Fraction Numbers
In the case of fractions, often we wait before explicitly introducing the idea of operating on fractions through addition and subtraction for quite some time due to the complexity of discussing “common denominators” and other complexities that must be unpacked.
However, if we are explicit about the unit of measure we are counting and/or operating with, things stay pretty easy.
Let’s consider adding the fractions ? + ?.
If we keep the unit of measure explicit, we get:
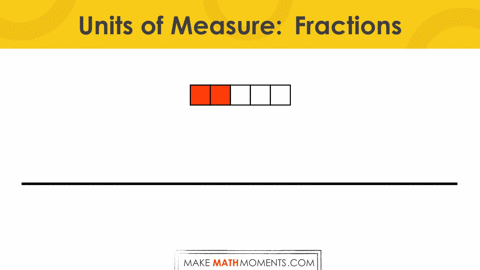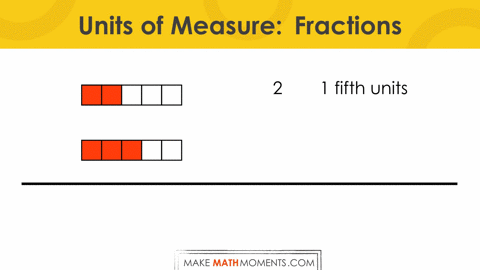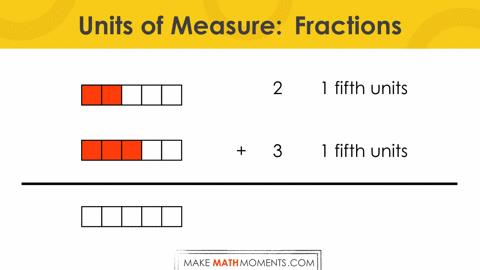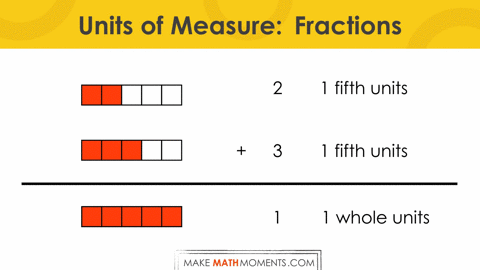
+ 3 1 fifth units
======================
5 1 fifth units
Here in Ontario, fraction addition is only explicitly introduced in grade 7. However, quite a bit earlier, students are exposed to the idea that adding two quantities with different units of measure (i.e.: metres and centimetres, or feet and inches) cannot be done unless one of the quantities is re-grouped or re-unitized to match the unit of measure of the other quantity. This is what we are doing when we ask students to find a common denominator. In this case, I think explicitly calling out the unit of measure – in this case, the unit fraction of “1 fifth units” – makes this idea more understandable conceptually.
Let’s keep going on to decimal numbers.
Decimal Numbers
Since decimal numbers are simply an abstract representation of a fraction, we can first introduce the idea of adding decimals by explicitly calling out the unit of measure and adding the quantity of each unit.
Let’s look at adding 0.2 + 0.3:
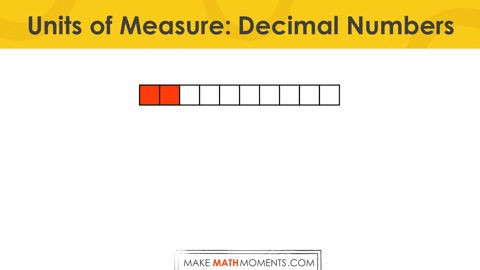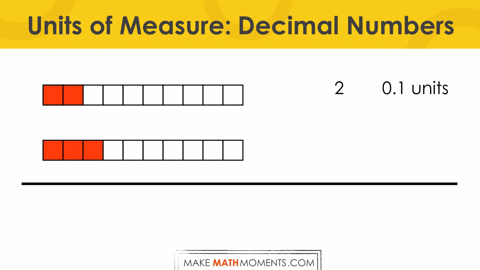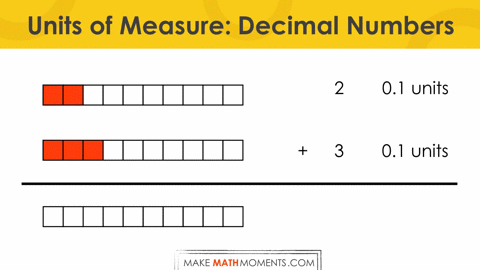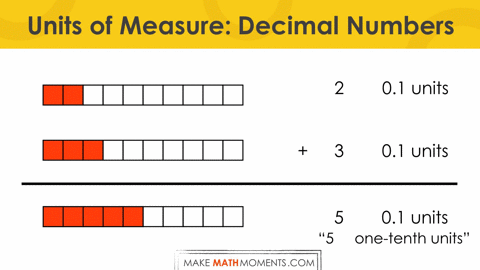
+ 3 0.1 units
==================
5 0.1 units
The beauty here again is that we are now adding 2 1-tenth units with another 3 1-tenth units for a total of 5 1-tenth units.
It’s like magic! Only not. It’s just math.
Algebra Addition
Let’s explore thinking about algebra and collecting like terms: 2x + 3x
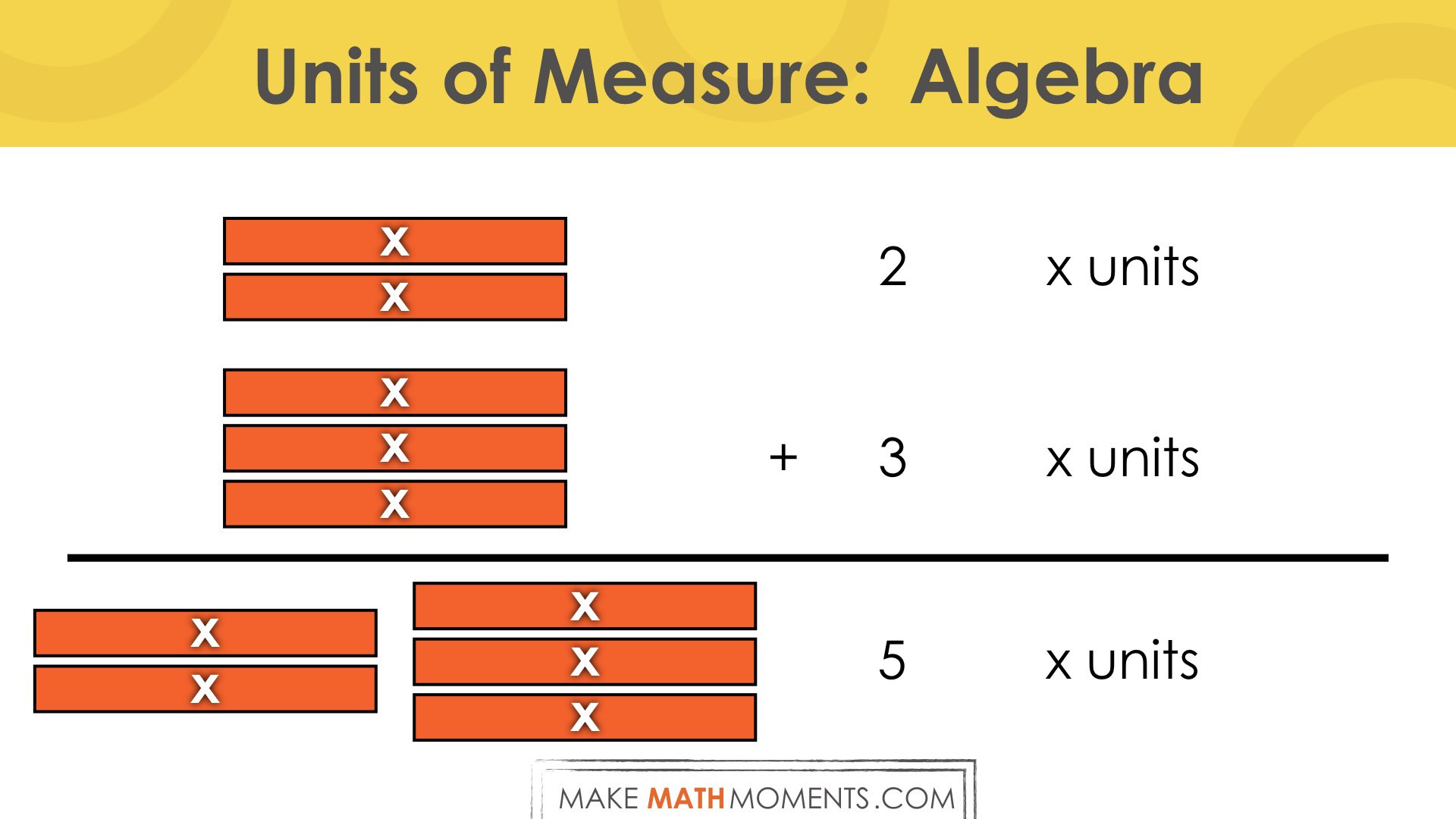
+ 3 x units
=================
5 x units
Consider that we’ve only shared examples of addition thus far. There are huge implications when we consider other operations like multiplication.
Multiplication
When we start viewing multiplication as the iteration of a single unit of measure, things start to get interesting.
For example, consider 2 x 3:
= 2 groups of 3
= 2 1 three units
= 2 threes
Rather than just thinking of multiplication as “2 groups of 3” alone, we can actually think of the quota (or quantity) of each group as the unit of measure. Now, 2 x 3 can be thought of as 2 1-threes or 2 threes.
Mathemagic.
Distributive Property
It doesn’t stop there.
Think of how intuitive number properties like the distributive property of multiplication can be thought of when we approach it like this.
Consider 3(2 + 4) or (2 x 3) + (4 x 3).
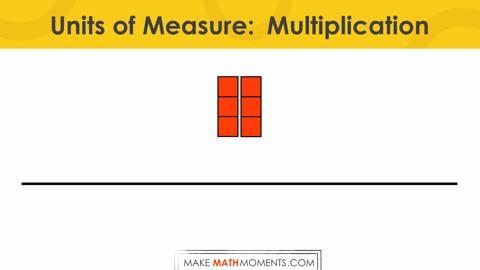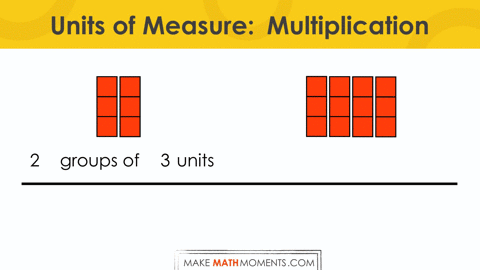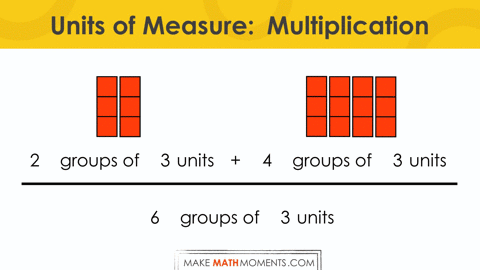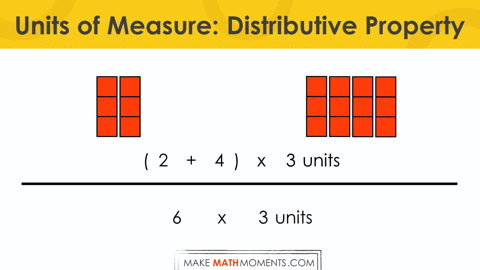
= 2 groups of 3 plus 4 groups of 3
= 2 threes + 4 threes
= 6 threes
= (2 + 4) threes
= (2 + 4) x 3
Mixing in the concrete/visual with the explicit articulation of the unit of measure and you’ve got yourself an opportunity to build some serious conceptual underpinnings!
Multiplying Fractions By A Whole Number
Let’s explore what this might look like for multiplying a fraction by a whole number: 2 groups of ¾.
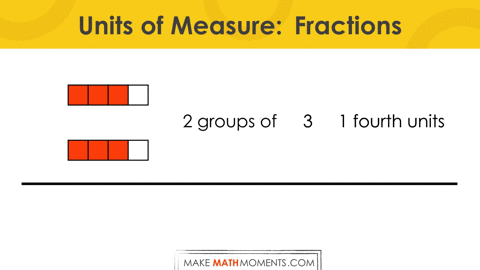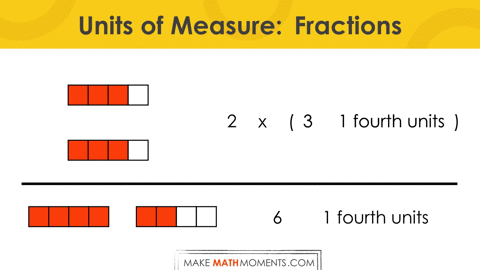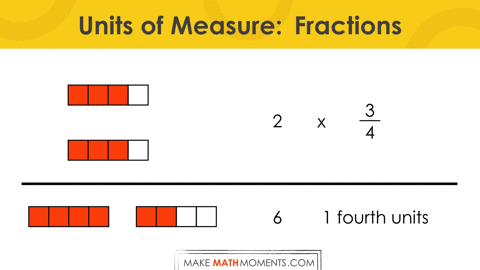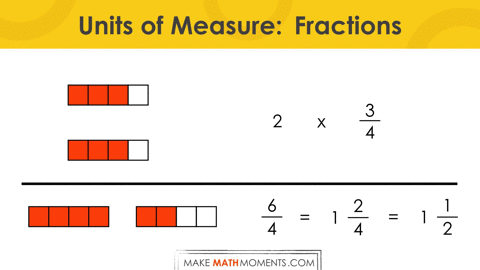
= 2 groups of ¾
= 2 groups of 3 fourths
= (3 fourths) + (3 fourths)
= 6 fourths
Not too bad, right?
For those of you interested in thinking through multiplying a fraction by a whole number; in other words, multiplying 3 fourth groups of 2 wholes, that might look like this:
¾ x 2
= ¾ groups of 2
= 3 fourths groups of two
= 3 fourths groups of one + 3 fourths groups of one
= 3 fourths + 3 fourths
= 6 fourths
Wait a second.
If I have 6 fourths, I can “combine” parts to make them all double the size leaving me with 3 halves.
If I have 3 halves and it takes 2 halves to make a whole, then I could also say I have 1 whole and 1 half remaining.
Multiplying A Fraction By A Fraction
How about multiplying a fraction by a fraction?
Well, let’s have a look at ½ groups of ¾.

½ x ¾
= ½ groups of ¾
= 1 half groups of 3 fourths
If I focus on my units of measure being 1 half groups of 3 fourths, I know very quickly that “1 whole group” has 3 fourths in it, but I only need to iterate “1 half” of that group.
Almost automatically, we can say that the result is 1 and ½ fourths or 1.5 fourths.
This is not a very conventional result, so let’s think about what we should do next with this unfriendly result.
If we partition our fourths into eighths, our 1 whole fourth becomes 2 whole eighths and our ½ fourth becomes 1 whole eighth.
Thus, revealing a more friendly, equivalent result of 3 eighths.
Not convinced that the unit of measure can be helpful in our pursuit of uncovering mathematics?
No problem! Let’s try division to see if that helps.
Dividing Fractions: Quotative Division
Let’s explore ¾ divided by ¼ in a quotative division scenario.

When we focus on the unit of measure (in this case, 1-fourths), it is easy to think of this problem as how many 1 wholes are there in 3 wholes. In a sense, we aren’t changing anything because we are in fact asking how many “1 whole” fourths there are in “3 whole” fourths.
This focus on the unit of measure can really help us better understand much of the work that most learn procedurally alone – like dividing fractions.
While things get a bit more hairy when we introduce fractions with uncommon denominators (i.e.: different units of measure), finding a common denominator takes care of that!
Let’s explore at ? divided by ½ also in a quotative situation.
? divided by ½
= 2 thirds divided by 1 half
Wait. We’re stuck in this different size parts situation. That’s no fun.
Let’s fix that.
= 2 third divided by 1 half
= 4 sixths divided by 3 sixths
Let’s be clear here. I have 4 parts that are a sixth of the original whole and I want to determine how many groups of 3 sixths there are (quotative division).
= 4 sixths divided by 3 sixths
= 4/3 groups
More specifically, since I’m thinking quotatively, I should say that there are 4/3 groups of 3 sixths in 4 sixths. Alternatively, there are 4/3 groups of ½ in ?.
Dividing Fractions: Partitive Division
I think it would be a complete rip-off if we didn’t also look at partitive division as well.
So, let’s first explore something fairly simple. In this case, ¾ divided by 1. Since it is partitive division, we would say how much of ¾ is in 1 whole group.
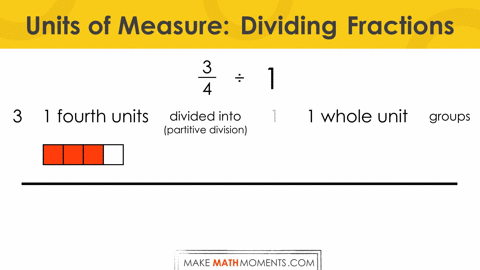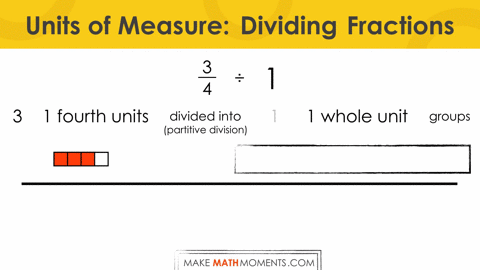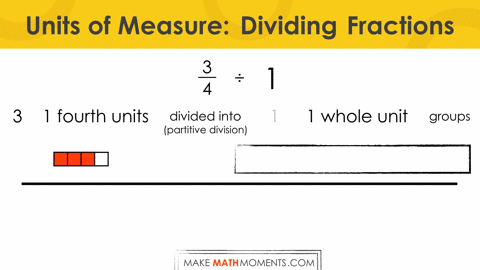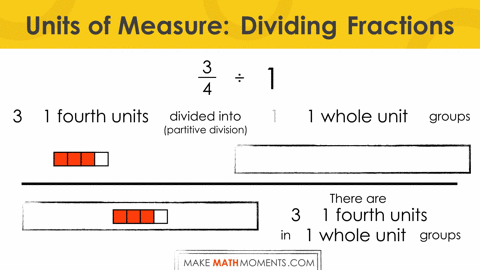
Now, let’s ramp it up a bit and work with ¾ divided by ¼ partitively. In other words, we are saying that there is ¾ in ¼ groups. If I think of this highlighting the unit of measure as 1-fourth, we could say that there are 3 fourths in 1 fourth groups. Since our unit of measure is the same, I can now just focus on the 3 “whole” fourths that are in 1 “whole” fourth groups to determine that there must be 3 in each group.
Alternatively, we can show this visually.
When thinking partitively, the goal is to determine how many are in 1 whole group, given a quantity (or total quota) and how many groups (or parts) the quantity is to be divided into.

Since the goal of partitive division is to determine the quota of 1 whole group, we must actually iterate (or scale) our 1 one-fourth of a group up to 4 one-fourth groups (or 1 whole group).
Our result is 12 one-fourths in 4 one-fourth groups or 3 wholes in 1 whole group.
Wow, that was a lot!
If you made it this far, then you’re clearly interested in how fractions (and other areas of mathematics) work conceptually with a focus on the unit of measure.
By all means I am not suggesting that thinking this way will be faster for students to come up with answers to problems. That’s what procedures are for.
What I am suggesting is that if you want to help students understand the mathematics they are engaging in with an end goal of building procedural fluency, then this would be a great place to invest some time in. When students (and we as teachers) are able to see the connections that exist in mathematics between big ideas, they are more readily able to see mathematics as an interconnected discipline that always makes sense.
Only then can we truly Make Math Moments That Matter for every student in our classroom for weeks, months, and even years.
Want to take the learning on the run?
Download the Complete Guide to dive straight in by .
Want To Explore The Unit Fraction With Your Students?
If you’re interested in exploring the importance of the unit fraction with your students, consider having them engage in one of the following versions of the “Baking Brownies” task:
OPTION A:
You are making 9 pans of brownies.
Each brownie needing 3 fourths cups of flour.
How many cups of flour is required in total?
OPTION B:
You are making 9 pans of brownies, each needing 1 half cups of flour.
How many cups of flour is required in total?
Want to grab the slides for the Baking Brownies tasks? Be sure to grab them here!
What was your biggest take-away from this new learning? How might you go about incorporating a focus on the unit of measure in your classroom?
If you try any of the above, be sure to let me know how it went in the comments!


Trackbacks/Pingbacks