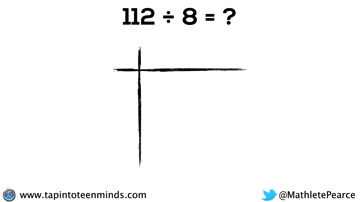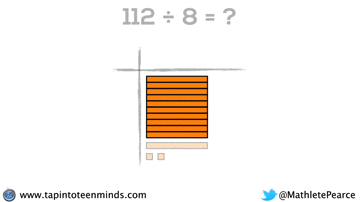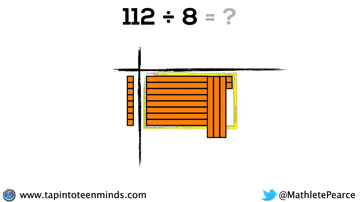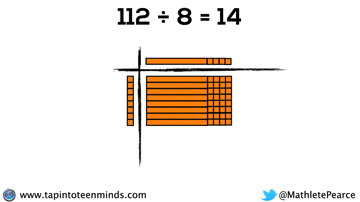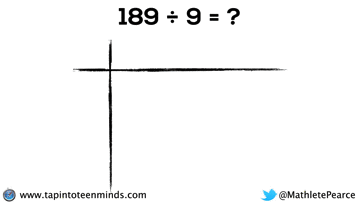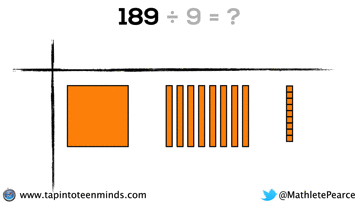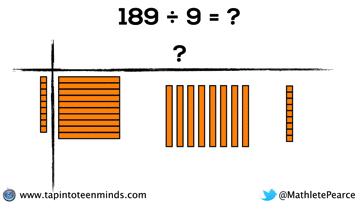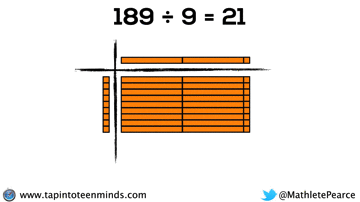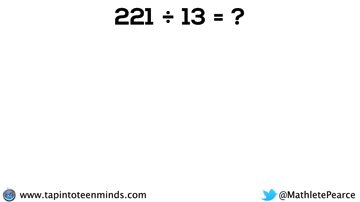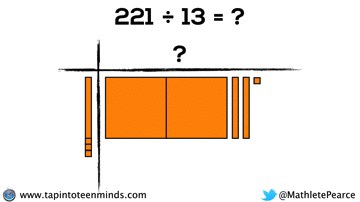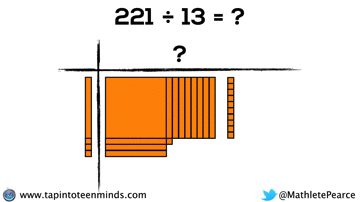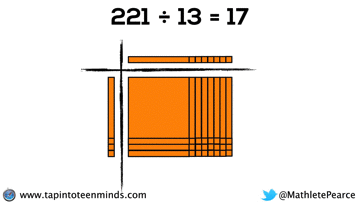PETL Math Professional Development Workshop
Saturday March 25th, 2017
Thanks for inviting me to learn with you on a Saturday in Peel! The group was energetic and excited to learn about meaningful manipulative use, counting principles, the progression of multiplication/division and the importance of concreteness fading!
Here’s a summary of what we explored today. Looking forward to connecting again soon!
After a brief presentation about avoiding the rush to the algorithm, we took some time to explore a 3 act math task with a very low-floor and high-ceiling, called the Airplane Problem:
[threeactshortcode the_query=”post_type=realworldmath&p=18652″]
In the airplane problem, we made predictions and made connections to subitizing and unitizing.
Counting Principles
We briefly discussed the importance of counting and quantity principles like subitizing and unitizing. A full summary is below:
[postshortcode the_query=”p=18603″]
Tiny Polka Dots
After break, I shared Daniel Finkel‘s game, Tiny Polka Dots. We made some connections between the counting and quantity principles and the different card decks in this game.
Also be sure to check out his TED Talk here.
Exploring the Progression of Multiplication
We made a leap from counting principles and unitizing to multiplication and specifically, using arrays and area models.
[postshortcode the_query=”p=17501″]
We also made a connection to “Japanese Multiplication” or “Stick Multiplication”:
[postshortcode the_query=”p=18762″]
3 Act Math Task: Donut Delight
After lunch, we explored the Donut Delight 3 act math task where we played with multiplication to predict how many donuts there were in the “double hundred dozen” box and then used repeated subtraction to lead to a flexible division algorithm for division when we tried to find how many layers there were.
[threeactshortcode the_query=”post_type=realworldmath&p=18719″]
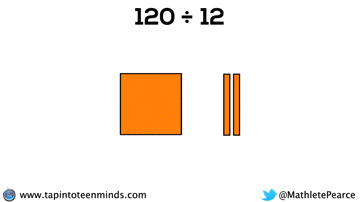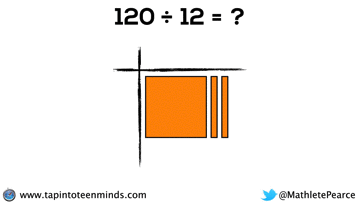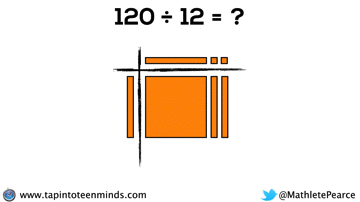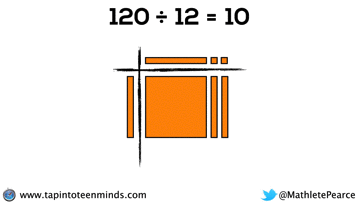
Progression of Division
We spent some time working with the progression of division in most groups as well. Here are some screenshots of what we looked at:
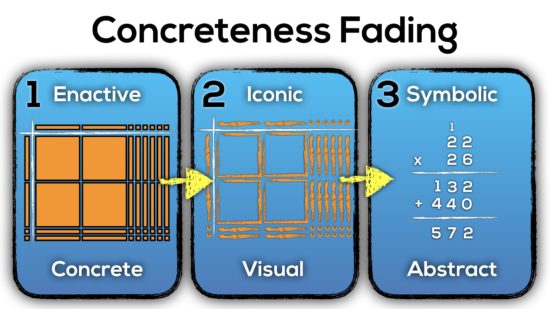
Concreteness Fading
We attempted to summarize the use of manipulatives on a continuum called “Concreteness Fading”. While the name suggests that concrete manipulatives fade away over time, it is important to remember that they fade away with one layer of abstraction and then reappear as a new layer is “piled” on.
Hope you folks found this professional learning experience useful.
I’d be delighted to come back and learn alongside you all again sometime soon!