How to Find the Surface Area of a Cone

Lateral Area of Cone Formula Explained

In the past, I have always engaged my students with interactive activities to help them understand how the formula for volume of a prism is related to the volume of a pyramid with the same base and height. However, until this year, I wasn’t quite sure how to explain the surface area of a cone formula without simply revealing it.

This year, I decided to get the students to engage in an activity to attempt finding the formula for surface area of a cone collaboratively and I was pleased with the result.

Math Topics Related To This Activity:

Finding area of composite figures,
finding the surface area of a cone, and
investigating geometric relationships.

Preparing for the Activity:

The activity portion simply involves different size pieces of paper for students to experiment making cones with. In this particular case, I created two different types of cut:

A square piece of paper cut diagonally in half, and
A rectangular piece of paper with a length significantly longer than the width.

: Square Piece of Paper

: Cutting the Square Paper Diagonally

Minds On:

Students in their table groups will use the square piece of paper to create a cone. Ensure students create the cone with paper “edge to edge” as to avoid overlapping and thus losing some of the surface area.

The teacher will then ask students to use the piece of paper to:

Find the surface area of the cone you created.

Are there any patterns or geometric relationships that you’ve found?

Some prompts for students:

Do you believe that there is a pattern or relationship? Discuss with your elbow partner.
What information do you feel will be important for you to find the surface area?

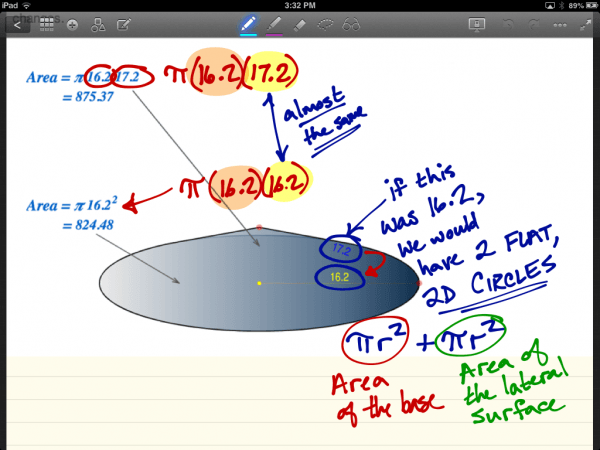
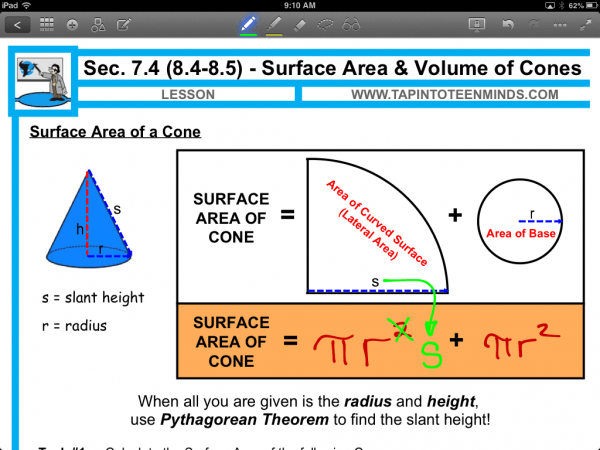
Often times, when using a square piece of paper, students predict that the surface area of a cone can be found using Pi times the radius-squared for the base plus a quarter of the area of the base since the net will appear to be a quarter of a circle. Or, algebraically:

Area of the Base + Lateral Area
= (Pi)r^2 + (Pi)(r^2)/4

However, if you give them a rectangular piece of paper, some students may realize that this will not work for every cone. This may lead to a deeper discussion about what we could do to their predicted formula to make it work for another cone. For example, if the lateral area represents 1/6 of the area of the base, then this might lead to students exploring further.

Action:

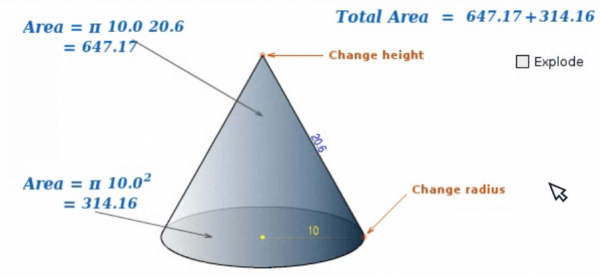
Students can then head to a Surface Area of a Cone Interactive Manipulative from Math Open Reference. The interactive widget allows users to change the height and radius of a cone to help them understand the formula.

Surface Area of a Short Cone

Surface Area of a Tall Cone

Students may notice that when the slant height is equal to the radius of the cone, the area of the base and the lateral area are equal. The formula for surface area of a cone in this situation could be determined as follows:

SA = Area of the Base + Lateral Area
= (Pi)(r^2) + (Pi)(r^2)
= 2(Pi)(r^2)

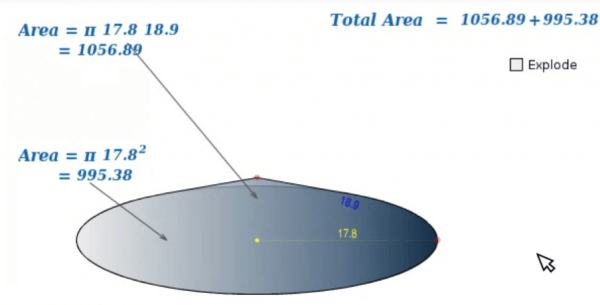
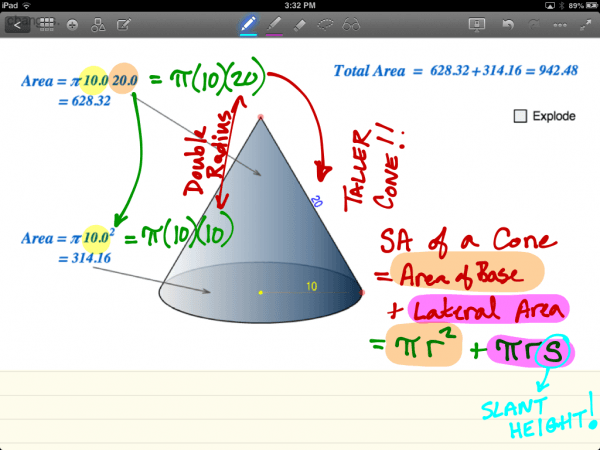
As the slant height increases without changing the dimensions of the radius, the lateral area becomes larger than the area of the base. Rather than having a radius equal to the slant height for the lateral portion of the cone, the slant height is increased causing the cone to get taller. This changes the formula slightly:

SA = Area of the Base + Lateral Area
= (Pi)(r^2) + (Pi)(r)(s)

In this activity, we usually introduce the volume of a cone as well, since we have already demonstrated the volume relationships between prisms and pyramids. Students apply their knowledge of this volume relationship: