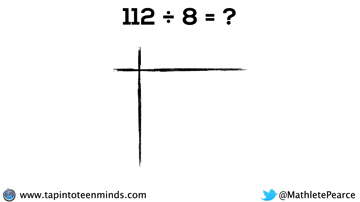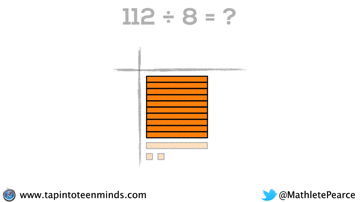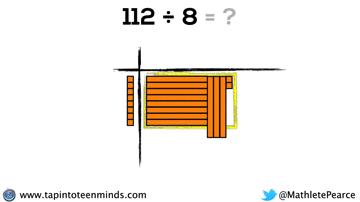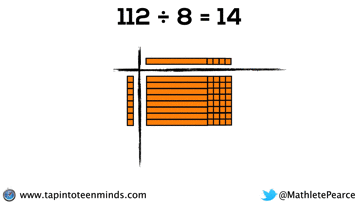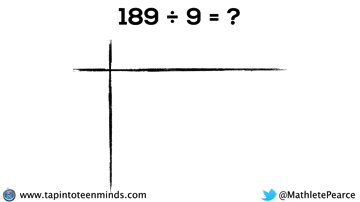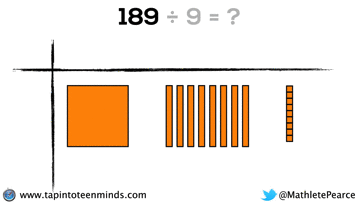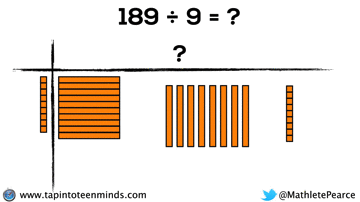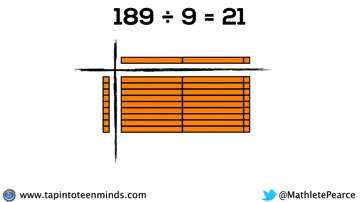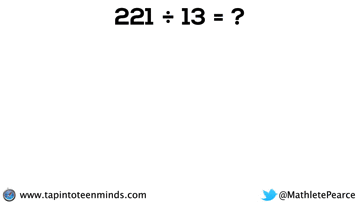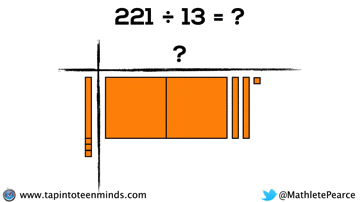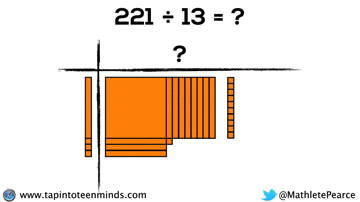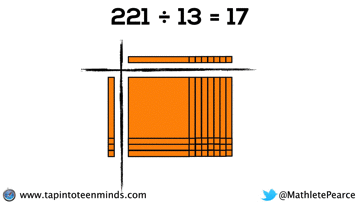GECDSB School Based Learning Sessions (SBL)
Monday March 6th, 2017
Thanks for inviting me to learn with you on your school based learning day! The group was energetic and excited to learn about meaningful manipulative use, spatial reasoning, some counting principles, visualizing numerical expressions, some multiplication/division and the importance of concreteness fading!
Here’s a summary of what we explored today throughout all three 100-minute blocks, noting that some groups went further in different areas than others:
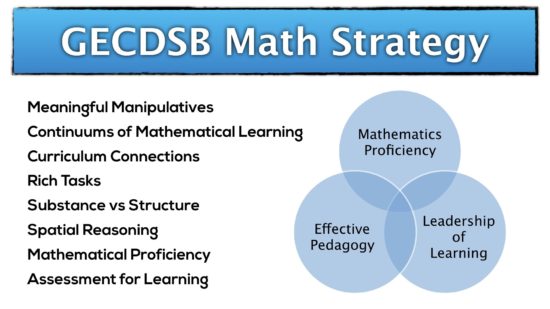
The GECDSB Mathematics Strategy
Mathematical Proficiencies
The full GECDSB Mathematics Vision is here.
Paying Attention to Spatial Reasoning
Warm-Up: How Do You See the Dots?
We did a quick Dot-Card warm-up asking you to visualize how you saw a series of dots on the screen. We went around the table and it seemed that everyone had a different perspective.
Here’s some of the ways you might have visualized the dots:
3 Act Math Task: Donut Delight
After a good consolidation of the dot plate task, we explored the Donut Delight 3 act math task where we played with multiplication to predict how many donuts there were in the “double hundred dozen” box and then used repeated subtraction to lead to a flexible division algorithm for division when we tried to find how many layers there were.
[threeactshortcode the_query=”post_type=realworldmath&p=18719″]
Most of the groups recognized division as the opposite operation to multiplication and noted the Japanese multiplication method that has been floating around on Twitter recently. Here’s a summary of it below:
[postshortcode the_query=”p=18762″]
While we didn’t explore the progression of multiplication explicitly, the following post might be useful to extend some of the thinking from the donut delight task.
[postshortcode the_query=”p=17501″]
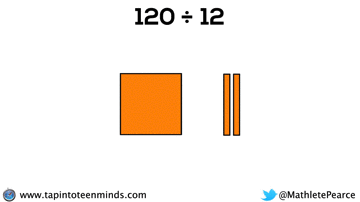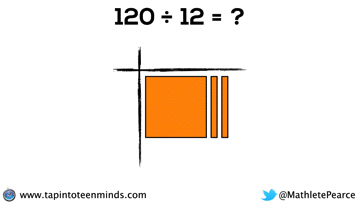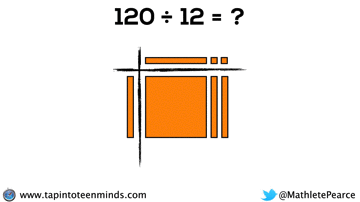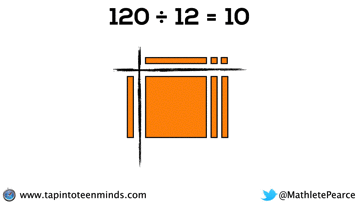
Progression of Division
We spent some time working with the progression of division in most groups as well. Here are some screenshots of what we looked at:
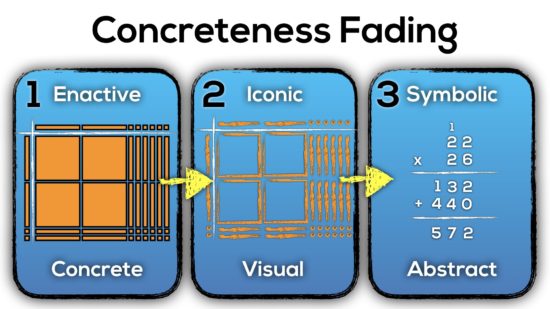
Concreteness Fading
We attempted to summarize the use of manipulatives on a continuum called “Concreteness Fading”. While the name suggests that concrete manipulatives fade away over time, it is important to remember that they fade away with one layer of abstraction and then reappear as a new layer is “piled” on.
Hope you folks found this professional learning experience useful.
I’d be delighted to come back and learn alongside you all again sometime soon!