GECDSB Mathematics Professional Development
Thanks for inviting me to learn with the John Campbell Math Team as you engage in your Math Leadership of Learning Practice (MLLP) work through the Mathematics Knowledge Network (MKN).
You can scroll down to see our past sessions, or consider jumping to the specific session you’re looking for:
Monday June 5th, 2017
Curriculum Deep Dive
After recapping what the group had discussed in the previous half day session, members of the team took a dive into the curriculum to attempt identifying areas where fractions and fractional thinking exists in their own grade level. Then, members shared out.
Some of the resources that were used included:
The Ontario Mathematics Curriculum, Grade 1 to 8
Number Sense and Numeration Curriculum Continuum by DSBN
Key Ideas of the Ontario Curriculum, Mathematics, Revised 2005, Kindergarten–Grade 8 by TDSB
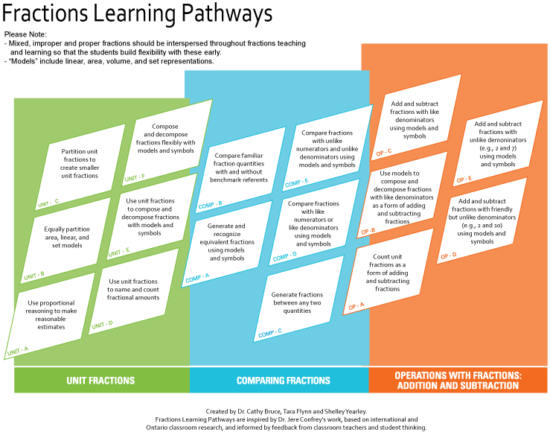
Fractions Learning Pathways
We then explored the Fractions Learning Pathways and related resources from the EduGains website:
Unit Fractions
Unit Fractions A – Use proportional reasoning to make reasonable estimates.
Unit Fractions B – Equally partition area, linear, and set models.
Unit Fractions C – Partition unit fractions to create smaller unit fractions.
Unit Fractions D – Use unit fractions to name and count fractional amounts.
Unit Fractions E – Use unit fractions to compose and decompose fractions with models and symbols.
Unit Fractions F – Compose and decompose fractions flexibly with models and symbols.
Comparing Fractions
Comparing Fractions A – Generate and recognize equivalent fractions using models and symbols.
Comparing Fractions B – Compare familiar fraction quantities with and without benchmark references.
Comparing Fractions C – Generate fractions between any two quantities.
Comparing Fractions D – Compare fractions with like numerators or like denominators using models and symbols.
Comparing Fractions E – Compare fractions with unlike numerators and unlike denominators using models and symbols.
Operations With Fractions
Operations With Fractions A – Count unit fractions as a form of adding and subtracting fractions.
Operations With Fractions B – Use models to compose and decompose fractions with like denominators as a form of adding and subtracting fractions.
Operations With Fractions C – Add and subtract fractions with like denominators using models and symbols.
Operations With Fractions D – Add and subtract fractions with friendly but unlike denominators (e.g., 2 and 10) using models and symbols.
Operations With Fractions E – Add and subtract fractions with unlike denominators (e.g., 2 and 7) using models and symbols.
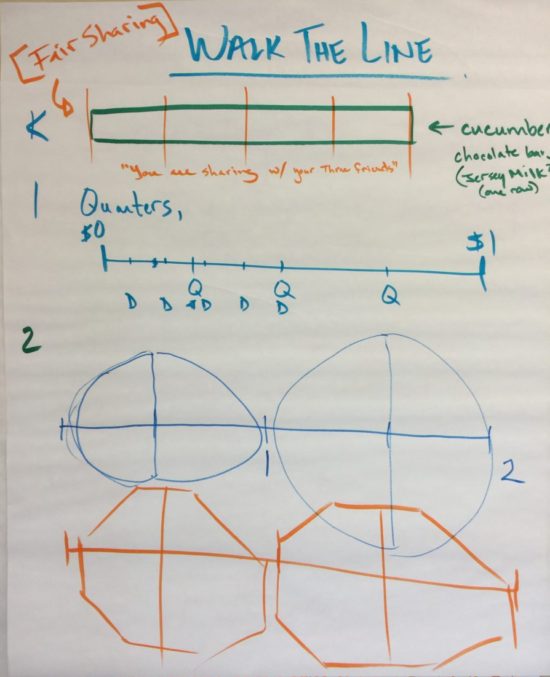
We spent some time planning out what a school-wide task involving Unit Fractions: A and the Walk Out Task from the resource page. Here is some of the brainstorming that took place:
We also watched a video of Cathy Bruce about Fractions and the importance of this work:
We also explored Fraction Constructs based on the work from the Paying Attention to Fractions document with some animated visuals to go with them:
[postshortcode the_query=”p=17492″]
Here are a few other resources that may be useful as we continue this work:
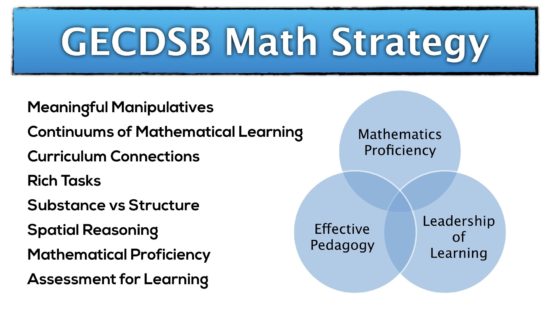
The GECDSB Mathematics Strategy
Mathematical Proficiencies
The full GECDSB Mathematics Vision is here.
Pedagogical System
Based on work by Glenda Anthony and Margaret Walshaw, the Pedagogical System is the result of a meta-analysis of many studies which are summarized into four key components:
You can also see a “silent solution” animation of the pedagogical system in detail:
Tuesday June 13th, 2017
Morning of MLLP Planning: Fractions Learning Pathways, Unit Fractions A
This morning, we spent a half day together trying to flesh out the next steps for the John Campbell Public School MLLP project. We all agreed that our short term plan might look something like this:
- Plan a school wide version of the Walk The Line task from Unit Fractions A of the Fractions Learning Pathway.
- Implement this task in the classrooms of the MLLP Team Member Classrooms and possibly in a handful of other classrooms as well.
- Collect assessment data through conversations, observations and product (i.e.: video, written and student work samples).
- Share the task and the student thinking at the end of year Professional Development day. Potentially do some student work analysis as a staff to engage in a discussion around “Why Fractions” and make a plan moving forward for next year.
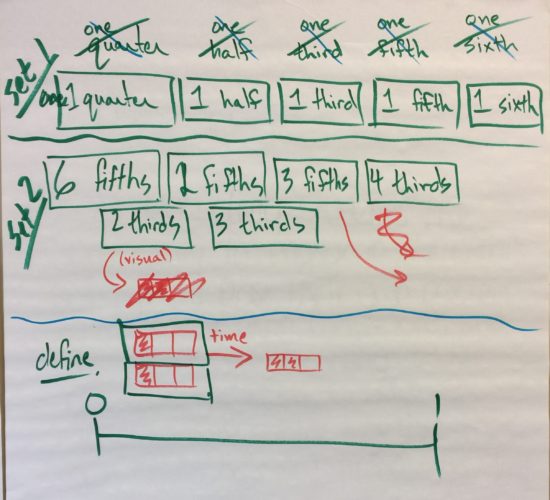
There was a lot of great discussion around unit fractions and how we might represent unit fractions orally and written in the classroom. For example, we discussed whether we might describe unit fractions in these ways:
- one half, three fourths, two thirds, and so on;
- 1 half, 3 fourths, 2 thirds, and so on; or,
- 1 one half, 3 one fourths, 2 one thirds, and so on.
We spent some time planning out the task. Here’s what it is looking like so far:

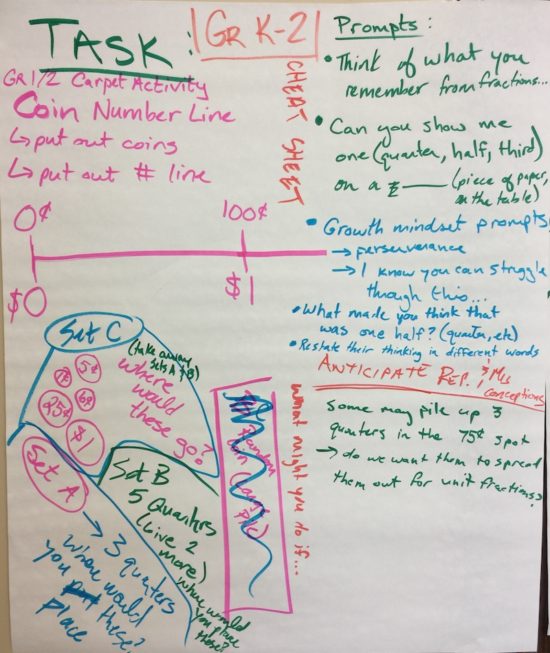
After nutrition break, we continued on the task planning journey and decided that the Walk The Line task could be used in its entirety from Grade 3 to grade 8 as a starting point to determine where students are in their learning relative to Unit Fractions, A.
We discussed the need for us to plan what sort of remediation activities one might consider if students are struggling with this activity. It was suggested that maybe the task be reused over a few weeks (say Fraction Fridays, maybe?) with different sets of fractions for students to organize on the number line.
The plan for Thursday will be to continue the Long Range Plan and to explore the PRIME assessment tool for Number Sense and Operation. I’ll bring a copy of this resource for exploration.
The following Tuesday, we will be together for the day where we will do some task moderation. Be sure to bring student thinking with you. The afternoon will be focused around explicitly planning the PD Day at the end of the month.
Thursday June 15th, 2017
Morning of MLLP Planning: Wrapping Up Unit Fractions A Task, Long-Range Planning & More
This morning, we spent another morning to flesh out the next steps for the John Campbell Public School MLLP project.
Walk This Way Task Updates/Improvements
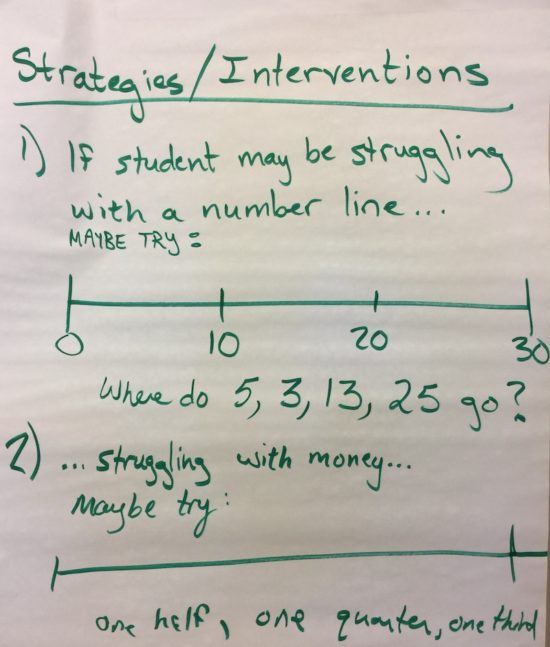
We did some recapping of the modified “Walk This Way” school wide problem and also brainstormed some of the student struggles that we might anticipate when doing the problem. Some of the team mentioned that our task might cause problems because students aren’t comfortable with number lines, while some may struggle because they aren’t comfortable working with money.
Here’s what we thought might be useful to consider when implementing the task:
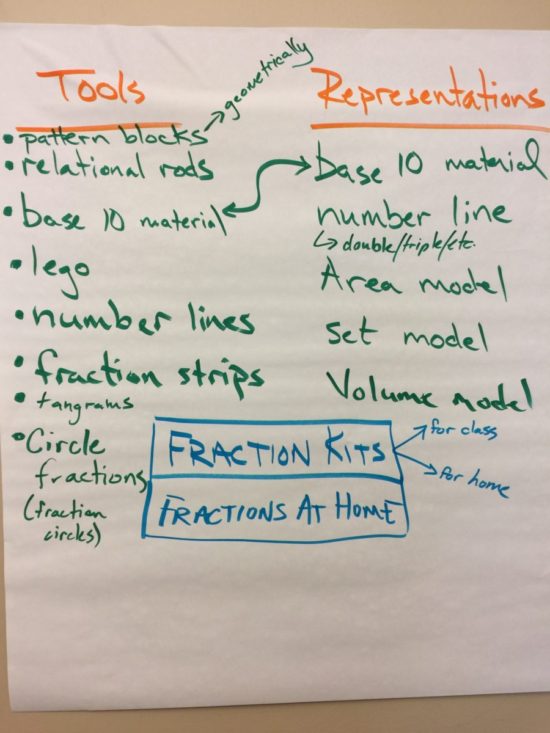
Oral, Written, Concrete and Visual Representations of Fractions
We spent some time discussing oral, written, concrete and visual representations of fractions and their importance. For example, we discussed how adding fractions can be made easier and more intuitive through the use of unit fractions.
Instead of simply teaching addition of fractions with symbolic notation as we might traditionally do:
2/5 + 1/5 = 3/5
We might first introduce this idea through unit fractions like this:
2 fifths + 1 fifth = 3 fifths
Notice how since the unit is “one fifth”, it seems more intuitive to add only the number of fifths (the numerator) instead of adding the denominator like some students often do when approaching this symbolically.
We also connected this idea to how we might use units to approach other ideas like distributive property in grade 4. Instead of:
5 x 4 = 2 x 4 + 3 x 4
We might first introduce this idea through units like this:
5 fours = 2 fours + 3 fours
Good conversation around this.
We also discussed a common problem that students encounter in their K-8 mathematical learning journey like:
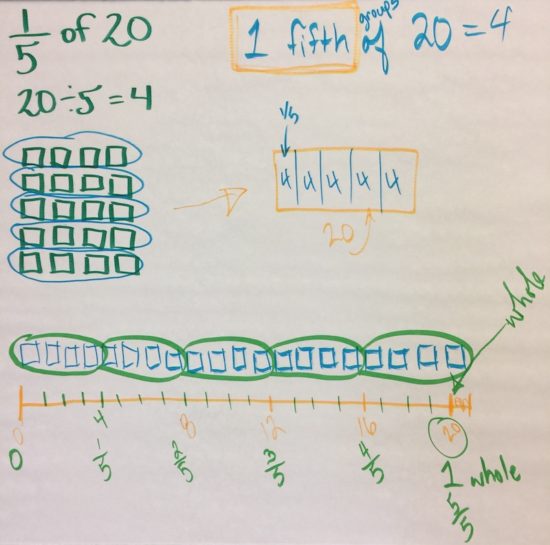
Find 1/5 of 20.
Most of us agreed that we commonly jump straight to a procedure here suggesting that “of” means multiply and a quick way to do this problem is by taking 20 and dividing by 5. Some teachers may even set this up as an equation and help students use opposite operations to solve this problem. All very useful skills to develop, however we often miss attempting to build some conceptual understanding to underpin these procedures.
Here’s a visual of some possible representations that could be used to build a conceptual understanding of this particular problem:
PRIME as a Possible Monitoring Tool
We also briefly explored and discussed PRIME as a possible assessment tool to help us monitor our work around the Fractions Learning Pathways. We discussed how Ann Pigeon (Ministry Education Officer) could help train us on using PRIME in our MLLP project.
End of June Professional Development Day Planning
When discussing the PD Day at the end of June, we discussed a possible minds on task involving different snacks and their various shapes and having small groups of teachers split them evenly amongst themselves.
For example, we might have opportunities to attack different concrete and contextual representations of fractions by using butter tarts (circular), candies (sets), Hershey chocolate bars (area), cucumbers (linear / number line), etc. Then, create groups of three, four, five and maybe even six teachers to take one (or more) of an item and split it evenly amongst the group. This could bring up some real interesting conversations around the importance of tools and representations in the math classroom around fractions specifically.
Life-Size Concept Map
We also briefly discussed doing some sort of life size concept map to record our thinking as we go along. Maybe take an entire wall and map out our learning as we go. Possibly even use marker students to try to show where they are in this big “web” of ideas that we are developing. What a cool way to make the professional learning visible in the school and to mobilize it across the staff.
- Might this be a bunch of chart paper on the wall?
- A wall painted in whiteboard paint?
- A wall painted in chalkboard paint?
- A wall that we can actually WRITE on with the idea that it would eventually be painted over?
…or are we just getting carried away? 🙂
Fraction Fridays
Could we possibly promote the use of fractions across the math curriculum (or even cross-curricular) on Fridays during the school year? More discussion needed around this, if that’s something you’d like to explore.
A Visual of the Long-Range Plan
Here’s what we’re thinking when it comes to the long-range plan for 2017-18.
Both Heidi and I are really excited about the great ideas coming from this group and we feel very fortunate to be a part of the great thinking.
Looking forward to our time together this coming Tuesday.