Begley Public School Based Learning SBL Math Professional Development

Begley Public School Based Learning (SBL)

GECDSB School Based Learning Sessions (SBL)

Jump to Professional Learning Sessions:

Thursday January 12th, 2017
Wednesday January 25th, 2017

Thursday January 12th, 2017

Thanks for inviting me to learn with you on your school based learning day! The group was energetic and excited to learn about meaningful manipulative use, spatial reasoning, concreteness fading and how they all fit with topics like fractions.

Here’s a summary of what we explored today:

The GECDSB Mathematics Strategy

$GECDSB Math Strategy$

Mathematical Proficiencies

The full GECDSB Mathematics Vision is here.

Warm-Up: How Do You See the Dots?

We did a quick Dot-Card warm-up asking you to visualize how you saw a series of dots on the screen. We went around the table and it seemed that everyone had a different perspective.

Here’s some of the ways you might have visualized the dots:

Tools and Representations

We discussed the importance of tools and representations to help students see mathematics from different perspectives. These quotes help us better understand some of the other important reasons tools and representations are so important:

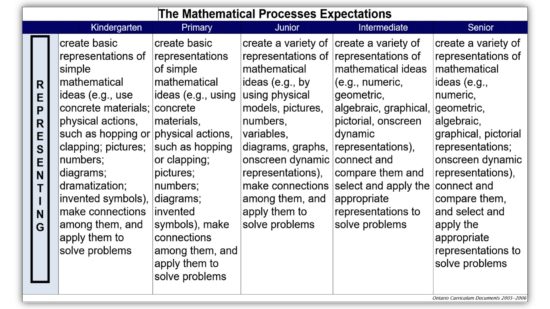
K-12 Process Expectations: Representing

We very briefly discussed the 7 Process Expectations in mathematics that are embedded throughout our K-12 Mathematics Curriculum and looked in particular at the expectations for Representing:

Task: The Sandwich Problem

With manipulatives on the table (square tiles, relational rods, cubes, pattern blocks and fake money) we attempted to find concrete and/or visual representations that could help us solve and justify the following task:

Original task was shared at a Ministry SIM Session. Here’s the slide deck.

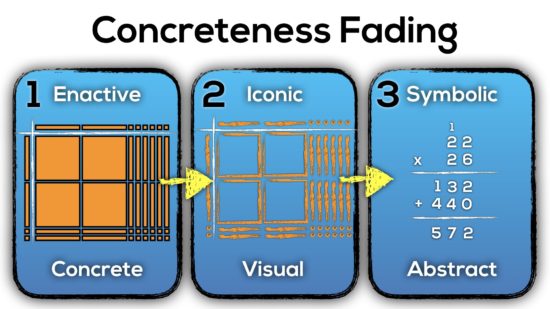
Concreteness Fading

We attempted to summarize the use of manipulatives on a continuum called “Concreteness Fading”. While the name suggests that concrete manipulatives fade away over time, it is important to remember that they fade away with one layer of abstraction and then reappear as a new layer is “piled” on.